安徽省阜阳市2020-2021学年七年级上学期数学第三次月考试卷
试卷更新日期:2021-07-01 类型:月考试卷
一、单选题
-
1. 在-9,0,2,-8这四个数中最小的是( )A、2 B、0 C、-8 D、-92. 下列图形中不是立体图形的是( )A、圆锥 B、圆柱 C、长方形 D、棱柱3. 一个数在数轴上的对应点到原点的距离为 .则这个数为( )A、 B、 C、 D、4. 用代数式表示“ 的3倍与 的差的平方”正确的是( )A、 B、 C、 D、5. 把方程 改写成用含 的代数式表示 的形式为( )A、 B、 C、 D、6. 下列说法正确的是( )A、过两点有且只有一条直线 B、 的次数是4 C、射线是直线的一半 D、若 ,则7. 如果 与 是同类项,则 , 的值分别是( )A、 B、 C、 D、8. 如图, 是 的中点, ,若 ,则线段 的长是( )
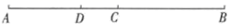 A、10 B、12 C、14 D、169. 已知关于 , 的二元一次方程组 的解满足 与 的值之和等于6,则 的值为( )A、8 B、 C、3 D、10. 如图,数轴上 , , 三点所表示的数分别为 , , .如果满足 且 ,那么下列各式表达错误的是( )
A、10 B、12 C、14 D、169. 已知关于 , 的二元一次方程组 的解满足 与 的值之和等于6,则 的值为( )A、8 B、 C、3 D、10. 如图,数轴上 , , 三点所表示的数分别为 , , .如果满足 且 ,那么下列各式表达错误的是( )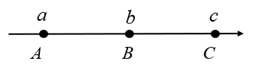 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 是线段 的中点,若 ,则线段 的长为 .12. 若 是关于 的方程 的解,则 的值是 .13. 伴随“互联网+”时代的来临,预计到2025年,我国各类网络互助平台的实际参与人数将达到450000000人,将数据450000000科学记数法表示为.14. 如图,线段 上的点数与线段的总数有如下关系:如果线段 上有3个点时,线段总共有3条;如果线段 上有4个点时,线段总共有6条;如果线段 上有5个点时,线段总共有10条;……
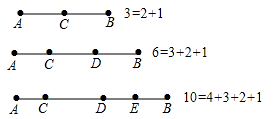 (1)、当线段 上有6个点时,线段总共有条.(2)、当线段 上有 个点时,线段总共有 . (用含 的代数式表示)条.
(1)、当线段 上有6个点时,线段总共有条.(2)、当线段 上有 个点时,线段总共有 . (用含 的代数式表示)条.三、解答题
-
15. 计算: .16. 解方程组: .17. 如图,已知线段 , , 是 的中点,求 的长.
 18. 为解决安徽省亳州市南北方向交通拥堵问题,亳州市政府决定再修建一条涡河隧道——汤王大道隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米.已知甲工程队平均每天比乙工程队多掘进5米.求甲、乙两个工程队平均每天分别掘进多少米?19. 已知甲、乙两人同时解关于 , 的二元一次方程组 ,甲解对了,得 ;乙写错了 ,得 ,试求方程组中 , , 的值.20. 如图, , 是线段 上的两点,已知 , , 分别为 , 的中点.
18. 为解决安徽省亳州市南北方向交通拥堵问题,亳州市政府决定再修建一条涡河隧道——汤王大道隧道,其中一段隧道贯穿工程由甲、乙两个工程队负责施工,甲工程队独立工作20天后,乙工程队加入,两工程队又联合工作5天,这25天共掘进425米.已知甲工程队平均每天比乙工程队多掘进5米.求甲、乙两个工程队平均每天分别掘进多少米?19. 已知甲、乙两人同时解关于 , 的二元一次方程组 ,甲解对了,得 ;乙写错了 ,得 ,试求方程组中 , , 的值.20. 如图, , 是线段 上的两点,已知 , , 分别为 , 的中点.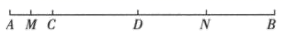 (1)、若 ,求 的长.(2)、若 ,求 的长.21. 某公园准备修建一块长为30米,宽为20米的长方形草坪,且要在草坪上修建如图所示的十字路,已知十字路宽 米,回答下列问题:
(1)、若 ,求 的长.(2)、若 ,求 的长.21. 某公园准备修建一块长为30米,宽为20米的长方形草坪,且要在草坪上修建如图所示的十字路,已知十字路宽 米,回答下列问题: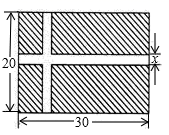 (1)、修建的十字路的面积是多少?(2)、草坪(阴影部分)的面积是多少?(3)、如果十字路宽1米,那么草坪(阴影部分)的面积是多少?22. 为响应政府“阳光体育”号召,西湖集团准备投入一部分资金,在西湖公园修建一批室外的乒乓球场和羽毛球场供市民免费使用.已知修建1个乒乓球场和2个羽毛球场共需要30万元,修建2个乒乓球场和5个羽毛球场共需要71万元.(1)、问修建1个乒乓球场和1个羽毛球场分别需要多少万元?(2)、西湖集团计划修建这样的乒乓球场和羽毛球场共11个,且投入资金刚好为100万元,问可以修建多少个羽毛球场?23. 如图,已知 , 是数轴上的两点, 为原点, ,且 .
(1)、修建的十字路的面积是多少?(2)、草坪(阴影部分)的面积是多少?(3)、如果十字路宽1米,那么草坪(阴影部分)的面积是多少?22. 为响应政府“阳光体育”号召,西湖集团准备投入一部分资金,在西湖公园修建一批室外的乒乓球场和羽毛球场供市民免费使用.已知修建1个乒乓球场和2个羽毛球场共需要30万元,修建2个乒乓球场和5个羽毛球场共需要71万元.(1)、问修建1个乒乓球场和1个羽毛球场分别需要多少万元?(2)、西湖集团计划修建这样的乒乓球场和羽毛球场共11个,且投入资金刚好为100万元,问可以修建多少个羽毛球场?23. 如图,已知 , 是数轴上的两点, 为原点, ,且 . (1)、数轴上 点对应的数为 , 点对应的数为 .(2)、若点 在数轴上对应的数为 ,且 点到 点, 点的距离之和为10,求 的值.(3)、若点 从点 出发,以每秒2个单位长度的速度沿数轴向右运动,设运动时间为 秒( ).
(1)、数轴上 点对应的数为 , 点对应的数为 .(2)、若点 在数轴上对应的数为 ,且 点到 点, 点的距离之和为10,求 的值.(3)、若点 从点 出发,以每秒2个单位长度的速度沿数轴向右运动,设运动时间为 秒( ).①在运动过程中,点 在数轴上表示的数是 . (用含 的代数式表示)
②当 时,求 的值.