初中数学浙教版八年级上册1.1 认识三角形 同步练习
试卷更新日期：2021-07-01 类型：同步测试
一、单选题
-
1. 下列长度的线段中，与长度为3，5的两条线段能组成三角形的是（ ）A、2 B、7 C、9 D、112. 如图，CM 是 的中线， 的周长比 的周长大 ， ，则 AC 的长为（ ）
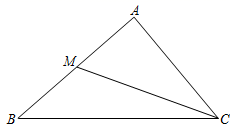A、 B、 C、 D、3. 如图，在 中，BC边上的高是（ ）
A、CD B、AE C、AF D、AH4. 已知△ABC中 ，则△ABC一定是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定5. 在三角形中，一定能将其面积分成相等两部分的是（ ）A、中线 B、高线 C、角平分线 D、某一边的垂直平分线6. 已知三角形的三边长分别为2、x、10，若x为正整数，则这样的三角形个数为（ ）A、1 B、2 C、3 D、47. 在△ABC中，∠A+∠B+∠C的度数为（ ）A、90° B、180° C、360° D、不确定8. 如果在 中， ，则 等于（ ）A、 B、 C、 D、9. 下列各组线段能组成一个三角形的是（ ）A、2cm，3cm，6cm B、6cm，8cm，10cm C、5cm，5cm，10cm D、4cm，6cm，10cm10. 已知三条线段长分别为2cm、4cm、acm ， 若这三条线段首尾顺次联结能围成一个三角形，那么a的取值可以是（ ）A、1cm B、2cm C、4cm D、7cm11. 为估计池塘两岸A、B间的距离，杨阳在池塘一侧选取了一点P，测得PA=16m，
PB=12m，那么AB间的距离不可能是（ ）.
A、5m B、15m C、20m D、28m12. 若 的三边长分别为整数，周长为11，且有一边长为4，则这个三角形的最大边长为（ ）A、7 B、6 C、5 D、413. 如图，将一副直角三角板如图所示放置，使含 角的三角板的一条直角边和含 角的三角板的一条直角边重合，则 的度数为（ ）
A、 B、 C、 D、14. 如图，∠B=∠C，则∠ADC与∠AEB的大小关系是（ ）
A、∠ADC>∠AEB B、∠ADC<∠AEB C、∠ADC=∠AEB D、大小关系不确定15. 如图，BE，CF都是△ABC的角平分线，且∠BDC=110°，则∠A的度数为（ ）
A、40° B、50° C、60° D、70°二、填空题
-
16. 若一个直角三角形的一条直角边长为 ， 另一条直角边是这条直角边的2倍，则这个直角三角形的面积为17. 已知 的三边长为2，7， ，请写出一个符合条件的 的整数值，这个值可以是.18. 如图， 是 的中线，点F在 上，延长 交 于点D.若 ，则 .
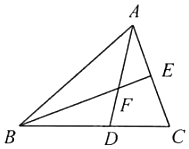19. 如图，已知AD⊥CD，BC⊥AC，垂足分别为D，C，且AB=4，CD=2，AD=3，则线段AC的取值范围为。
20. 如图所示的网格是正方形网格， 是网格线交点，则 的面积与 的面积的大小关系为： （填“>”，“=”或“<”） .
21. 已知三角形ABC，且AB＝3厘米，BC＝2厘米，A、C两点间的距离为x厘米，那么x的取值范围是 ．22. 如图所示，在△ABC中，∠1＝∠2，G是AD的中点，延长BG交AC于点E，F为AB上一点，CF⊥AD交AD于点H．①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH为△ACD的边AD上的高；④AH是△ACF的角平分线和高线，其中判断正确的有 ．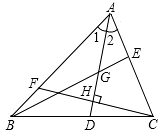
23. 如图，DE⊥AB，∠A＝25°，∠D＝45°，则∠ACB的度数为
24. 在一个三角形中，如果一个内角是另一内角的n倍（n为整数），那么我们称这个三角形为n倍三角形．如果一个三角形既是2倍角三角形，又是3倍角三角形，那么这个三角形最小的内角度数为 ．25. 在△ABC中，已知∠A = 100°，∠B = 60°，则∠C = .26. 若等腰三角形中有两边长分别为2和5，则这个三角形的周长为 .27. 当三角形中一个内角β是另一个内角a的 时，我们称此三角形为“希望三角形”，其中内角a称为“希望角”.如果一个“希望三角形”中有一个内角为54°，那么这个“希望三角形”的“希望角”度数为 .三、计算题
