初中数学浙教版九年级上册1.4 二次函数的应用 同步练习
试卷更新日期:2021-06-30 类型:同步测试
一、单选题
-
1. 二次函数 的图象与x轴交点的个数为( )A、0个 B、1个 C、2个 D、1个或2个2. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )
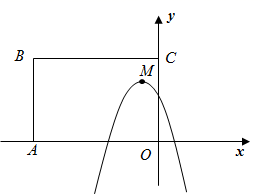 A、 B、 C、 D、3. 如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )
A、 B、 C、 D、3. 如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )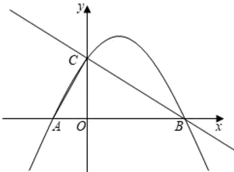 A、h> B、0<h≤ C、h>2 D、0<h<24. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、535. 已知一次函数 ,二次函数 ,对于x的同一个值,这两个函数所对应的函数值分别为 和 ,则下列表述正确的是( )A、 B、 C、 D、 , 的大小关系不确定6. 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )A、20 B、1508 C、1550 D、15587. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为 ,由此可知小宇此次实心球训练的成绩为( )
A、h> B、0<h≤ C、h>2 D、0<h<24. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为( )人A、56 B、55 C、54 D、535. 已知一次函数 ,二次函数 ,对于x的同一个值,这两个函数所对应的函数值分别为 和 ,则下列表述正确的是( )A、 B、 C、 D、 , 的大小关系不确定6. 便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=-2(x-20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是( )A、20 B、1508 C、1550 D、15587. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为 ,由此可知小宇此次实心球训练的成绩为( ) A、 米 B、8米 C、10米 D、2米8. 实数a,b,c满足4a﹣2b+c=0,则( )A、b2﹣4ac>0 B、b2﹣4ac≥0 C、b2﹣4ac<0 D、b2﹣4ac≤09. 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有( )
A、 米 B、8米 C、10米 D、2米8. 实数a,b,c满足4a﹣2b+c=0,则( )A、b2﹣4ac>0 B、b2﹣4ac≥0 C、b2﹣4ac<0 D、b2﹣4ac≤09. 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有( )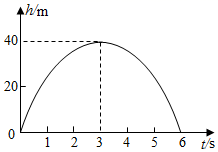 A、①② B、②③ C、①③④ D、①②③10. 二次函数y=x2+2kx+k2﹣1(k为常数)与x轴的交点个数为( )A、1 B、2 C、0 D、无法确定11. 小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 ,则小明此次成绩为( )A、8米 B、10米 C、12米 D、14米12. 如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A、①② B、②③ C、①③④ D、①②③10. 二次函数y=x2+2kx+k2﹣1(k为常数)与x轴的交点个数为( )A、1 B、2 C、0 D、无法确定11. 小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数 ,则小明此次成绩为( )A、8米 B、10米 C、12米 D、14米12. 如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( ) A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系13. 已知抛物线 与x轴的一个交点为 ,则代数式 的值为( )A、2018 B、2019 C、2020 D、202114. 已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴的负半轴相交.则下列关于 、 的大小关系正确的是( )A、 B、 C、 D、15. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、
A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系13. 已知抛物线 与x轴的一个交点为 ,则代数式 的值为( )A、2018 B、2019 C、2020 D、202114. 已知二次函数 的图象与 轴交于点 、 ,且 ,与 轴的负半轴相交.则下列关于 、 的大小关系正确的是( )A、 B、 C、 D、15. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、二、填空题
-
16. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度 与水平距离 之间的关系为 ,由此可知铅球推出的距离是m.17. 以初速度v(单位:m/s)从地面竖直向上抛出小球,从抛出到落地的过程中,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=vt﹣4.9t2.现将某弹性小球从地面竖直向上抛出,初速度为v1 , 经过时间t1落回地面,运动过程中小球的最大高度为h1(如图1);小球落地后,竖直向上弹起,初速度为v2 , 经过时间t2落回地面,运动过程中小球的最大高度为h2(如图2).若h1=2h2 , 则t1:t2=.
 18. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.19. 已知抛物线 与 轴的一个交点的横坐标大于1且小于2,则m的取值范围是 .20. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .
18. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.19. 已知抛物线 与 轴的一个交点的横坐标大于1且小于2,则m的取值范围是 .20. 如图,直线 与抛物线 交于点 ,且点A在y轴上,点B在x轴上,则不等式 的解集为 .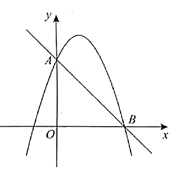 21. 一个球从地面上竖直向上弹起的过程中,距离地面高度 (米)与经过的时间 (秒)满足以下函数关系: ,则该球从弹起回到地面需要经过秒,距离地面的最大高度为米.22. 如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.
21. 一个球从地面上竖直向上弹起的过程中,距离地面高度 (米)与经过的时间 (秒)满足以下函数关系: ,则该球从弹起回到地面需要经过秒,距离地面的最大高度为米.22. 如图,在平面直角坐标系中,抛物线 与y轴交于点A,过点A作x轴的平行线交抛物线于点M,P为抛物线的顶点,若直线OP交直线AM于点B,且M为线段AB的中点,则a的值为.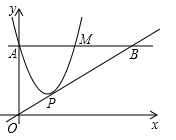 23. 如图,已知直线 分别交 轴、 轴于点 、 ,点 是抛物线 上的一个动点,其横坐标为 .过点 且平行于 轴的直线与直线 交于点 ,当 时, 的值是 .
23. 如图,已知直线 分别交 轴、 轴于点 、 ,点 是抛物线 上的一个动点,其横坐标为 .过点 且平行于 轴的直线与直线 交于点 ,当 时, 的值是 . 24. 如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式 ,则沙包在飞行过程中距离地面的最大高度是米.
24. 如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式 ,则沙包在飞行过程中距离地面的最大高度是米. 25. 二次函数y=ax2+bx+c的图象与y轴交于点(0,-3),与x轴两个交点的横坐标分别为m,n,则a(m2+n2)+b(m+n)的值为
25. 二次函数y=ax2+bx+c的图象与y轴交于点(0,-3),与x轴两个交点的横坐标分别为m,n,则a(m2+n2)+b(m+n)的值为三、计算题
-
26. 已知函数y=2x2-(3-k)x+k2-3k-10的图象经过原点,试确定k的值。
四、解答题
-
27. 如图,一个边长为 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 中,点G、E、F分别在 、 、 上,且 .在 、 、五边形 三个区域上种植不同的花卉,每平方米的种植成本分别是20元、20元、10元.问:点E在什么位置时,正方形花坛种植花卉所需的总费用最少,最少为多少元?
 28. 某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?
28. 某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?五、综合题
-
29. 某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高x元.(1)、服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?(2)、当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?30. 某公司计划组织员工去武夷山风景区三日游,人数估计在 人.已知某旅行社的收费方案为:如果人数超过20人且不超过30人,人均收费为1000元;如果超过30人且不超过50人,则每增加1人,人均收费降低10元.设该公司旅游人数为x(人),人均收费为y(元).(1)、求y与x之间的关系式;.(2)、若旅行社此次带团的导游工资和车辆等固定成本为6000元,游客的吃住和门票等其他成本为600元/人.请你分析:旅行社带团接待旅游人数多少人时,旅行社所获利润w(元)最大,最大利润是多少?(利润=总收费-固定成本-其他成本)
-