2021年高考数学真题试卷(新高考Ⅱ卷)
试卷更新日期:2021-06-30 类型:高考真卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 复数 在复平面内对应的点所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 设集合 ,则 ( )A、 B、 C、 D、3. 抛物线 的焦点到直线 的距离为 ,则 ( )A、1 B、2 C、 D、44. 北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步卫星的轨道位于地球赤道所在平面,轨道高度为 (轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为 的球,其上点A的纬度是指 与赤道平面所成角的度数.地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为 ,记卫星信号覆盖地球表面的表面积为 (单位: ),则S占地球表面积的百分比约为( )A、26% B、34% C、42% D、50%5. 正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )A、 B、 C、 D、6. 某物理量的测量结果服从正态分布 ,下列结论中不正确的是( )A、 越小,该物理量在一次测量中在 的概率越大 B、 越小,该物理量在一次测量中大于10的概率为0.5 C、 越小,该物理量在一次测量中小于9.99与大于10.01的概率相等 D、 越小,该物理量在一次测量中落在 与落在 的概率相等7. 已知 ,则下列判断正确的是( )A、 B、 C、 D、8. 已知函数 的定义域为 , 为偶函数, 为奇函数,则( )A、 B、 C、 D、
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 下列统计量中,能度量样本 的离散程度的是( )A、样本 的标准差 B、样本 的中位数 C、样本 的极差 D、样本 的平均数10. 如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足 的是( )A、
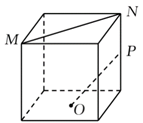 B、
B、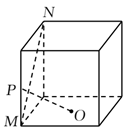 C、
C、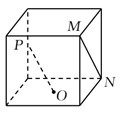 D、
D、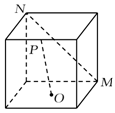 11. 已知直线 与圆 ,点 ,则下列说法正确的是( )A、若点A在圆C上,则直线l与圆C相切 B、若点A在圆C内,则直线l与圆C相离 C、若点A在圆C外,则直线l与圆C相离 D、若点A在直线l上,则直线l与圆C相切12. 设正整数 ,其中 ,记 .则( )A、 B、 C、 D、
11. 已知直线 与圆 ,点 ,则下列说法正确的是( )A、若点A在圆C上,则直线l与圆C相切 B、若点A在圆C内,则直线l与圆C相离 C、若点A在圆C外,则直线l与圆C相离 D、若点A在直线l上,则直线l与圆C相切12. 设正整数 ,其中 ,记 .则( )A、 B、 C、 D、三、填空题:本题共4小题,每小题5分,共20分.
-
13. 已知双曲线 ,离心率 ,则双曲线C的渐近线方程为 .14. 写出一个同时具有下列性质①②③的函数 .
① ;②当 时, ;③ 是奇函数.
15. 已知向量 , 则 .16. 已知函数 ,函数 的图象在点 和点 的两条切线互相垂直,且分别交y轴于M,N两点,则 取值范围是 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
17. 记 是公差不为0的等差数列 的前n项和,若 .(1)、求数列 的通项公式 ;(2)、求使 成立的n的最小值.18. 在 中,角A,B,C所对的边长分别为 .(1)、若 ,求 的面积;(2)、是否存在正整数a,使得 为钝角三角形?若存在,求出a的值;若不存在,说明理由.19. 在四棱锥 中,底面 是正方形,若 .
 (1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.20. 已知椭圆C的方程为 ,右焦点为 ,且离心率为 .(1)、求椭圆C的方程;(2)、设M,N是椭圆C上的两点,直线 与曲线 相切.证明:M,N,F三点共线的充要条件是 .
(1)、证明:平面 平面 ;(2)、求二面角 的平面角的余弦值.20. 已知椭圆C的方程为 ,右焦点为 ,且离心率为 .(1)、求椭圆C的方程;(2)、设M,N是椭圆C上的两点,直线 与曲线 相切.证明:M,N,F三点共线的充要条件是 .