浙江省2021年中考数学真题分类汇编13 统计与概率
试卷更新日期：2021-06-29 类型：二轮复习
一、单选题
-
1. 下列事件中，属于不可能事件的是（ ）A、经过红绿灯路口，遇到绿灯 B、射击运动员射击一次，命中靶心 C、班里的两名同学，他们的生日是同一天 D、从一个只装有白球和红球的袋中摸球，摸出黄球2. 甲、乙、丙、丁四名射击运动员进行射击测试，每人10次射击成绩的平均数 （单位：环）及方差 （单位：环 ）如下表所示：
甲
乙
丙
丁
9
8
9
9
1.6
0.8
3
0.8
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（ ）
A、甲 B、乙 C、丙 D、丁3. 5月1日至7日，我市每日最高气温如图所示，则下列说法错误的是（ ）
A、中位数是33℃ B、众数是33℃ C、平均数是 ℃ D、4日至5日最高气温下降幅度较大4. 超市货架上有一批大小不一的鸡蛋，某顾客从中选购了部分大小均匀的鸡蛋，设货架上原有鸡蛋的质量（单位：g）平均数和方差分别为 ，s2 ， 该顾客选购的鸡蛋的质量平均数和方差 ，s12 ， 则下列结论一定成立的是（ ）A、 ＜ B、 ＞ C、s2＞s12 D、s2＜s125. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人，则初中生有（ ）某天参观温州数学名人馆的学生人数统计图
A、45人 B、75人 C、120人 D、300人6. 在一个不透明的袋中装有6个只有颜色不同的球，其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球，是白球的概率为（ ）A、 B、 C、 D、7. 一个布袋里放有3个红球和2个白球，它们除颜色外其余都相同.从布袋中任意摸出1个球，摸到白球的概率是（ ）A、 B、 C、 D、8. 某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是（ ）A、 B、 C、 D、二、填空题
-
9. 一个不透明的袋中装有21个只有颜色不同的球，其中5个红球，7个白球，9个黄球.从中任意摸出1个球是红球的概率为.10. 一个不透明的袋子里装有3个红球和5个黑球，它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为.11. 为庆祝建党100周年，某校举行“庆百年红歌大赛”.七年级5个班得分分别为85，90，88，95，92，则5个班得分的中位数为分.12. 某商场举办有奖销售活动，每张奖券被抽中的可能性相同。若以每1000张奖券为一个开奖单位，设5个一等奖，15个二等奖，不设其它奖项，则只抽1张奖券恰好中奖的概率是13. 看了《田忌赛马》故事后，小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为 ．
马匹
姓名
下等马
中等马
上等马
齐王
6
8
10
田忌
5
7
9
14. 某单位组织抽奖活动，共准备了150张奖券，设一等奖5个，二等奖20个，三等奖80个.已知每张奖券获奖的可能性相同，则1张奖券中一等奖的概率是.15. 一个不透明布袋中有2个红球，1个白球，这些球除颜色外无其他差别，从中随机摸出一个小球，该小球是红色的概率为 .16. 现有甲、乙两种糖果的单价与千克数如下表所示甲种糖果
乙种糖果
单价(元/千克)
30
20
千克数
2
3
将这2千克甲种糖果盒3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为元/千克
三、综合题
-
17. 为了更好地了解党的历史，宣传党的知识，传颂英雄事迹，某校团支部组建了：A.党史宣讲；B.歌曲演唱；C.校刊编撰；D.诗歌创作等四个小组，团支部将各组人数情况制成了如下统计图表（不完整）：
各组参加人数情况统计表
小组类别
A
B
C
D
人数（人）
10
a
15
5
各组参加人数情况扇形统计图
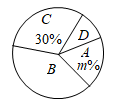
根据统计图表中的信息，解答下列问题：
(1)、求m的值；(2)、求扇形统计图中D所对应的圆心角度数；(3)、若在某一周各小组平均每人参与活动的时间如下表所示：小组类别
A
B
C
D
平均用时（小时）
2.5
3
2
3
求这一周四个小组所有成员平均每人参与活动的时间。
18. 某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2021年初的视力数据，并调取该批学生2020年初的视力数据，制成如下统计图（不完整）：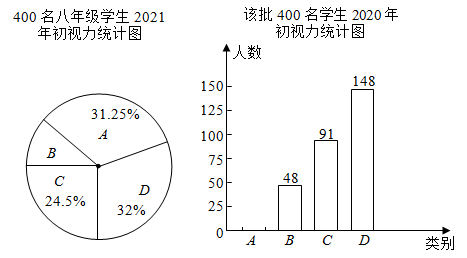
青少年视力健康标准
类别
视力
健康状况
A
视力≥5.0
视力正常
B
4.9
轻度视力不良
C
4.6≤视力≤4.8
中度视力不良
D
视力≤4.5
重度视力不良
根据以上信息，请解答：
(1)、分别求出被抽查的400名学生2021年初轻度视力不良（类别B）的扇形圆心角度数和2020年初视力正常（类别A）的人数．(2)、若2021年初该市有八年级学生2万人，请估计这些学生2021年初视力正常的人数比2020年初增加了多少人？(3)、国家卫健委要求，全国初中生视力不良率控制在69%以内．请估计该市八年级学生2021年初视力不良率是否符合要求？并说明理由．19. 某校将学生体质健康测试成绩分为 ， ， ， 四个等级，依次记为4分，3分，2分，1分.为了解学生整体体质健康状况，拟抽样进行统计分析.(1)、以下是两位同学关于抽样方案的对话：小红：“我想随机柚取七年级男、女生各60人的成绩.”
小明：“我想随机柚取七、八、九年级男生各40人的成绩.”
根据右侧学校信息，请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩，请给出抽样方案.
学校共有七、八、九三个年级学生近千人，各段人数相近，每段男、女生人数相当，
.....
(2)、现将随机抽取的测试成绩整理并绘制成如下统计图，请求出这组数据的平均数、中位数和众数.某校部分学生体质健康测试成绩统计图
20. 绍兴莲花落，又称“莲花乐”，“莲花闹”，是绍兴一带的曲艺.为了解学生对该曲种的熟悉度，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成如下不完整的统计图.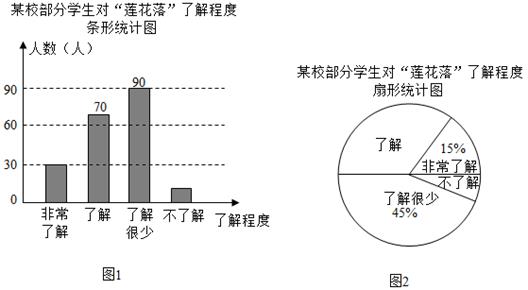
根据图中信息，解答下列问题：
(1)、本次接受问卷调查的学生有多少人？并求图2中“了解”的扇形圆心角的度数.(2)、全校共有1200名学生，请你估计全校学生中“非常了解”、“了解”莲花落的学生共有多少人.21. 图1表示的是某书店今年1～5月的各月营业总额的情况，图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况.若该书店1～5月的营业总额一共是182万元，观察图1、图2，解答下列向题：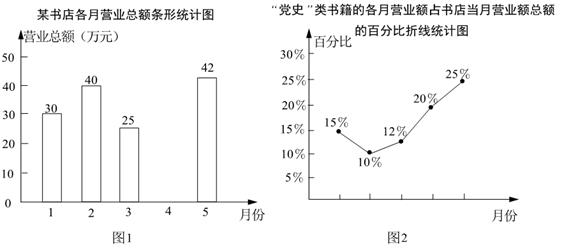
(1)、求该书店4月份的营业总额，并补全条形统计图.(2)、求5月份“党史”类书籍的营业额.(3)、请你判断这5个月中哪个月“党史”类书籍的营业额最高，并说明理由.22. 小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如下测试成绩折线统计图.根据图中信息，解答下列问题：
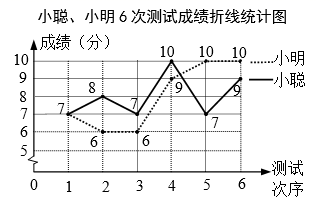(1)、要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 （单位：平方分）.根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由.23. 为进一步做好“光盘行动”，某校食堂推出“半份菜”服务，在试行阶段，食堂对师生满意度进行抽样调查.并将结果绘制成如下统计图（不完整）.
(1)、求被调查的师生人数，并补全条形统计图，(2)、求扇形统计图中表示“满意”的扇形圆心角度数.(3)、若该校共有师生1800名，根据抽样结果，试估计该校对食堂“半份菜”服务“很满意”或“满意”的师生总人数.24. 杨梅果实成熟期正值梅雨季节，雨水过量会导致杨梅树大量落果，给果农造成损失.为此，市农科所开展了用防雨布保护杨梅果实的实验研究.在某杨梅果园随机选择40棵杨梅树，其中20棵加装防雨布（甲组），另外20棵不加装防雨布（乙组）.在杨梅成熟期，统计了甲、乙两组中每一棵杨梅树的落果率（落地的杨梅颗数占树上原有杨梅颗数的百分比），绘制成如下统计图表（数据分组包含左端值不包含右端值）.甲组杨梅树落果率频数分布表
落果率
组中值
频数（棵）
0≤x＜10%
5%
12
10%≤x＜20%
15%
4
20%≤x＜30%
25%
2
30%≤x＜40%
35%
1
40%≤x＜50%
45%
1
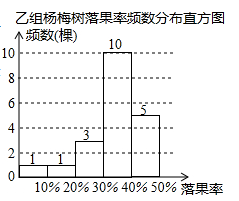(1)、甲、乙两组分别有几棵杨梅树的落果率低于20%？(2)、请用落果率的中位数或平均数，评价市农科所“用防雨布保护杨梅果实”的实际效果；(3)、若该果园的杨梅树全部加装这种防雨布，落果率可降低多少？说出你的推断依据.25. 为了解某校某年级学生一分钟跳绳情况，对该年级全部360名学生进行一分钟跳绳次数的测试，并把测得数据分成四组，绘制成如图所示的频数表和未完成的频数直方图（每一组不含前一个边界值，含后一个边界值）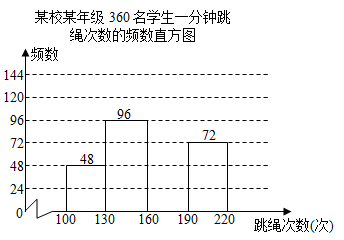
某校某年级360名学生一分钟跳绳次数的频数表
组别（次）
频数
100~130
48
130~160
96
160~190
a
190~220
72
(1)、求 的值；(2)、把频数直方图补充完整；(3)、求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比。