浙江省2021年中考数学真题分类汇编10 图形的变换与视图
试卷更新日期:2021-06-29 类型:二轮复习
一、单选题
-
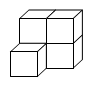
1. 用五个相同的正方体搭成如图所示的立体图形,则该立体图形的主视图是( )
 A、
A、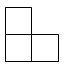 B、
B、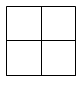 C、
C、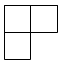 D、
D、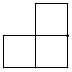 2. 直六棱柱如图所示,它的俯视图是( )
2. 直六棱柱如图所示,它的俯视图是( ) A、
A、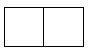 B、
B、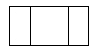 C、
C、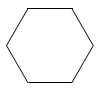 D、
D、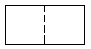 3. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )
3. 如图的几何体由五个相同的小正方体搭成,它的主视图是( )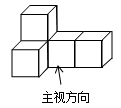 A、
A、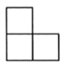 B、
B、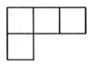 C、
C、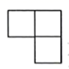 D、
D、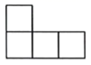 4. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
4. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )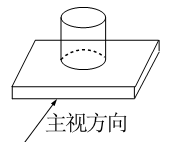 A、
A、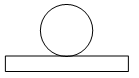 B、
B、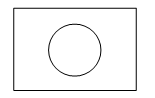 C、
C、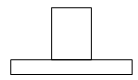 D、
D、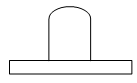 5. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
5. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )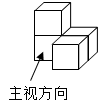 A、
A、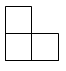 B、
B、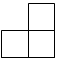 C、
C、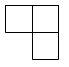 D、
D、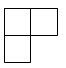 6. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )
6. 如图.将菱形ABCD绕点A逆时针旋转 得到菱形 , .当AC平分 时, 与 满足的数量关系是( )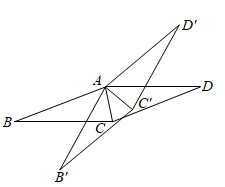 A、 B、 C、 D、7. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、 B、 C、 D、7. 如图,将长、宽分别为12cm,3cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )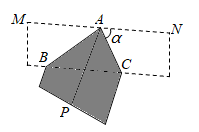 A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm28. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )
A、(36 )cm2 B、(36 )cm2 C、24cm2 D、36cm28. 将一张三角形纸片按如图步骤①至④折叠两次得图⑤,然后剪出图⑤中的阴影部分,则阴影部分展开铺平后的图形是( )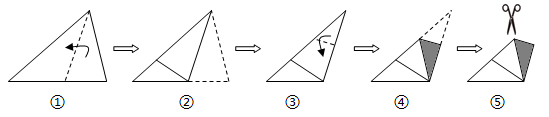 A、等腰三角形 B、直角三角形 C、矩形 D、菱形
A、等腰三角形 B、直角三角形 C、矩形 D、菱形二、填空题
-
9. 如图,将线段AB绕点A顺时针旋转30°,得到线段AC.若AB=12,则点B经过的路径 长度为 .(结果保留π)
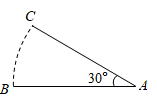 10. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。
10. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF。若MF=AB,则∠DAF=度。 11. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.
11. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.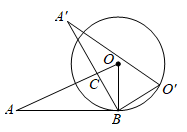 12. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .
12. 如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知 , .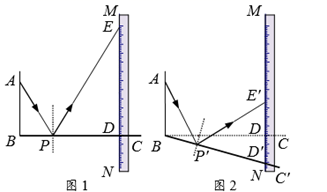 (1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.13. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
(1)、ED的长为.(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 (如图2),点P的对应点为 , 与MN的交点为D′,从A点发出的光束经平面镜 反射后,在MN上的光点为 .若 ,则 的长为.13. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.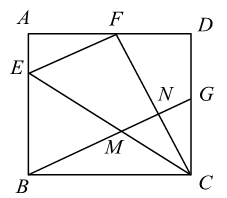
三、解答题
-
14. 如图 与 的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).
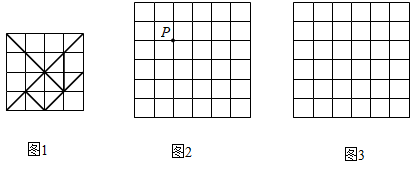 (1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.15. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .
(1)、选一个四边形画在图2中,使点 为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)、选一个合适的三角形,将它的各边长扩大到原来的 倍,画在图3中.15. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .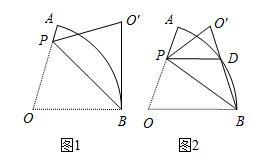 (1)、如图1,若 ,且 与 所在的圆相切于点B.
(1)、如图1,若 ,且 与 所在的圆相切于点B.①求 的度数.
②求AP的长.
(2)、如图2, 与 相交于点D,若点D为 的中点,且 ,求 的长.16. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .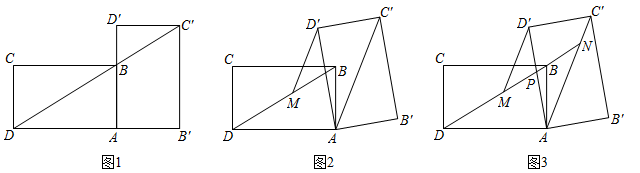
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
17. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).