浙江省2021年中考数学真题分类汇编09 圆
试卷更新日期:2021-06-29 类型:二轮复习
一、单选题
-
1. 已知扇形的半径为6,圆心角为 .则它的面积是( )A、 B、 C、 D、2. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )
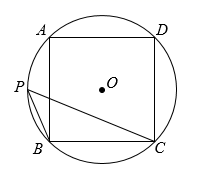 A、 B、 C、 D、3. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切4. 如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A、 B、 C、 D、3. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切4. 如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( ) A、60° B、70° C、80° D、90°5. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1 , 当点P运动时,点C1页随之运动。若点P从点A运动到点D,则线段CC1扫过的区域面积是
A、60° B、70° C、80° D、90°5. 如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结BP,点C关于直线BP的对称点为C1 , 当点P运动时,点C1页随之运动。若点P从点A运动到点D,则线段CC1扫过的区域面积是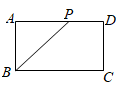 A、π B、 C、 D、
A、π B、 C、 D、二、填空题
-
6. 如图,将线段AB绕点A顺时针旋转30°,得到线段AC.若AB=12,则点B经过的路径 长度为 .(结果保留π)
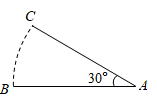 7. 如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2。若PT是⊙O的切线,T为切点,连结OT,则PT=
7. 如图,已知⊙O的半径为1,点P是⊙O外一点,且OP=2。若PT是⊙O的切线,T为切点,连结OT,则PT=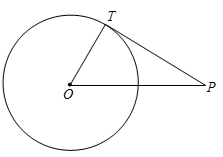 8. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.9. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.
8. 若扇形的圆心角为 ,半径为17,则扇形的弧长为.9. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.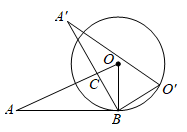 10. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )
10. 抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如示意图, 分别与 相切于点C,D,延长 交于点P.若 , 的半径为 ,则图中 的长为 .(结果保留 )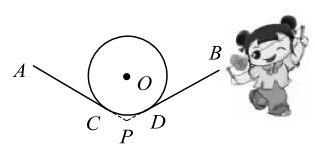 11. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
11. 如图,在△ABC中,∠BAC=30°,∠ACB=45°,AB=2,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP , 点A关于直线CP的对称点为A′,连结A′C , A′P . 在运动过程中,点A′到直线AB距离的最大值是;点P到达点B时,线段A′P扫过的面积为 .
三、综合题
-
12. 如图,已知AB是⊙O的直径,∠ACD是 所对的圆周角,∠ACD=30°。
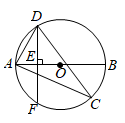 (1)、求∠DAB的度数;(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F。若AB=4,求DF的长。13. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.
(1)、求∠DAB的度数;(2)、过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F。若AB=4,求DF的长。13. 如图1,点C是半圆O的直径AB上一动点(不包括端点), ,过点C作 交半圆于点D,连结AD,过点C作 交半圆于点E,连结EB.牛牛想探究在点C运动过程中EC与EB的大小关系.他根据学习函数的经验,记 , , .请你一起参与探究函数 、 随自变量x变化的规律.通过几何画板取点、画图、测量,得出如下几组对应值,并在图2中描出了以各对对应值为坐标的点,画出了不完整图象.
x … 0.30 0.80 1.60 2.40 3.20 4.00 4.80 5.60 … … 2.01 2.98 3.46 3.33 2.83 2.11 1.27 0.38 … … 5.60 4.95 3.95 2.96 2.06 1.24 0.57 0.10 … 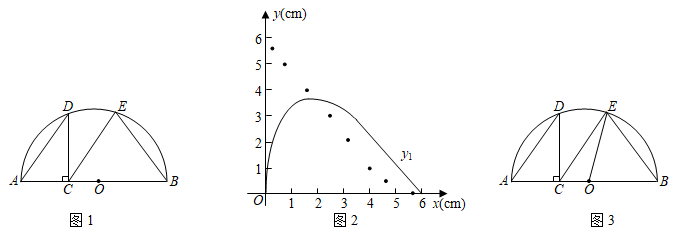 (1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.14. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .
(1)、当 时, =.(2)、在图2中画出函数 的图象,并结合图象判断函数值 与 的大小关系.(3)、由(2)知“AC取某值时,有 ”.如图3,牛牛连结了OE,尝试通过计算EC,EB的长来验证这一结论,请你完成计算过程.14. 在扇形 中,半径 ,点P在OA上,连结PB,将 沿PB折叠得到 .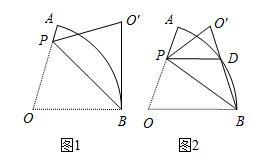 (1)、如图1,若 ,且 与 所在的圆相切于点B.
(1)、如图1,若 ,且 与 所在的圆相切于点B.①求 的度数.
②求AP的长.
(2)、如图2, 与 相交于点D,若点D为 的中点,且 ,求 的长.15. 如图,BD是半径为3的⊙O的一条弦,BD=4 ,点A是⊙O上的一个动点(不与点B,D重合),以A,B,D为顶点作▱ABCD. (1)、如图2,若点A是劣弧 的中点.
(1)、如图2,若点A是劣弧 的中点.①求证:▱ABCD是菱形;
②求▱ABCD的面积.
(2)、若点A运动到优弧 上,且▱ABCD有一边与⊙O相切.①求AB的长;
②直接写出▱ABCD对角线所夹锐角的正切值.
16. 如图,在平面直角坐标系中, 经过原点 ,分别交 轴、 轴于 , ,连结 .直线 分别交 于点 , (点 在左侧),交 轴于点 ,连结 .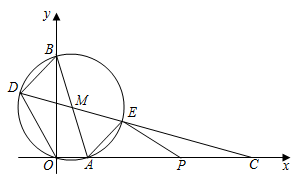 (1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.
(1)、求 的半径和直线 的函数表达式.(2)、求点 , 的坐标.(3)、点 在线段 上,连结 .当 与 的一个内角相等时,求所有满足条件的 的长.17. 如图1,四边形 内接于 , 为直径, 上存在点E,满足 ,连结 并延长交 的延长线于点F, 与 交于点G.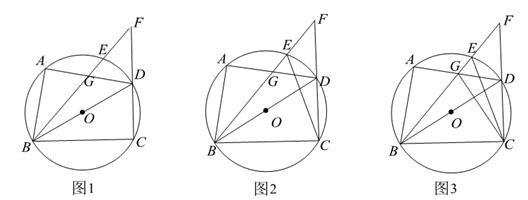 (1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .
(1)、若 ,请用含 的代数式表列 .(2)、如图2,连结 .求证; .(3)、如图3,在(2)的条件下,连结 , .①若 ,求 的周长.
②求 的最小值.