浙江省2021年中考数学真题分类汇编08 四边形

试卷更新日期：2021-06-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 5$ ， $B C = 6$ ，点D，E，F分别是AB，BC，CA的中点，连结DE，EF，则四边形ADEF的周长为（）

A、6 B、9 C、12 D、15

查看试题解析
2. 如图.将菱形ABCD绕点A逆时针旋转 $∠ α$ 得到菱形 $A B^{'} C^{'} D^{'}$ ， $∠ B = ∠ β$ .当AC平分 $∠ B^{'} A C^{'}$ 时， $∠ α$ 与 $∠ β$ 满足的数量关系是（）

A、 $∠ α = 2 ∠ β$ B、 $2 ∠ α = 3 ∠ β$ C、 $4 ∠ α + ∠ β = 180 °$ D、 $3 ∠ α + 2 ∠ β = 180 °$

查看试题解析
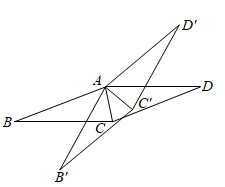3. 如图，菱形ABCD中， $∠ B = 60 °$ ，点P从点B出发，沿折线 $B C - C D$ 方向移动，移动到点D停止.在 $△ A B P$ 形状的变化过程中，依次出现的特殊三角形是（）

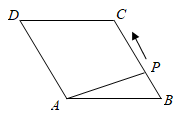A、直角三角形→等边三角形→等腰三角形→直角三角形 B、直角三角形→等腰三角形→直角三角形→等边三角形 C、直角三角形→等边三角形→直角三角形→等腰三角形 D、等腰三角形→等边三角形→直角三角形→等腰三角形

查看试题解析
4. 数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形放置，可得到更多的菱形.如图2，用2个相同的菱形放置，得到3个菱形.下面说法正确的是（）

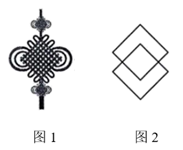A、用3个相同的菱形放置，最多能得到6个菱形 B、用4个相同的菱形放置，最多能得到16个菱形 C、用5个相同的菱形放置，最多能得到27个菱形 D、用6个相同的菱形放置，最多能得到41个菱形

查看试题解析
5. 如图是一个由5张纸片拼成的 $▱ A B C D$ ，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为 $S_{1}$ ，另两张直角三角形纸片的面积都为 $S_{2}$ ，中间一张矩形纸片 $E F G H$ 的面积为 $S_{3}$ ， $F H$ 与 $G E$ 相交于点O.当 $△ A E O ， △ B F O ， △ C G O ， △ D H O$ 的面积相等时，下列结论一定成立的是（）

A、 $S_{1} = S_{2}$ B、 $S_{1} = S_{3}$ C、 $A B = A D$ D、 $E H = G H$

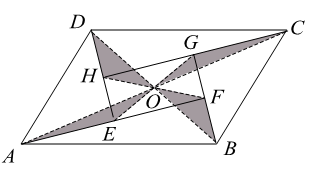查看试题解析
6. 由四个全等的直角三角形和一个小正方形组成的大正方形 $A B C D$ 如图所示.过点 $D$ 作 $D F$ 的垂线交小正方形对角线 $E F$ 的延长线于点 $G$ ，连结 $C G$ ，延长 $B E$ 交 $C G$ 于点 $H$ .若 $A E = 2 B E$ ，则 $\frac{C G}{B H}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\sqrt{2}$ C、 $\frac{3 \sqrt{10}}{7}$ D、 $\frac{3 \sqrt{5}}{5}$

查看试题解析

二、填空题

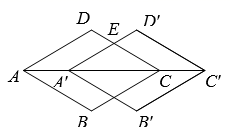
7. 如图，菱形 $A B C D$ 的边长为 $6 cm$ ， $∠ B A D = 60 °$ ，将该菱形沿AC方向平移 $2 \sqrt{3} cm$ 得到四边形 $A^{'} B^{'} C^{'} D^{'}$ ， $A^{'} D^{'}$ 交CD于点E，则点E到AC的距离为 $cm$ .

查看试题解析
8. 如图，在▱ABCD中，对角线AC ， BD交于点O ， AB⊥AC ， AH⊥BD于点H ，若AB＝2，BC＝2 $\sqrt{3}$ ，则AH的长为．

查看试题解析
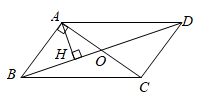9. 为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星（A，B，C，D，E是正五边形的五个顶点），则图中∠A的度数是度

查看试题解析
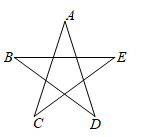10. 图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的 $d$ 的值为；记图1中小正方形的中心为点 $A$ ， $B$ ， $C$ ，图2中的对应点为点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ .以大正方形的中心 $O$ 为圆心作圆，则当点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 在圆内或圆上时，圆的最小面积为.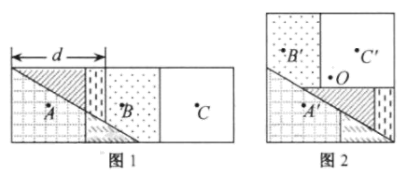

查看试题解析

三、解答题

11. 如图，在 $▱ A B C D$ 中， $E$ ， $F$ 是对角线 $B D$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $∠ A E B = ∠ C F D = 90 °$ .

(1)、求证：四边形 $A E C F$ 是平行四边形.

(2)、当 $A B = 5$ ， $\tan ∠ A B E = \frac{3}{4}$ ， $∠ C B E = ∠ E A F$ 时，求 $B D$ 的长.

查看试题解析
12. 如图，在7×7的正方形网格中，网格线的交点称为格点，点A ， B在格点上，每一个小正方形的边长为1．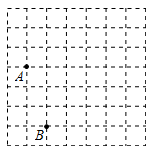

(1)、以AB为边画菱形，使菱形的其余两个顶点都在格点上（画出一个即可）．

(2)、计算你所画菱形的面积．

查看试题解析
13. 如图是由边长为1的小正方形构成的 $6 \times 4$ 的网格，点A，B均在格点上.

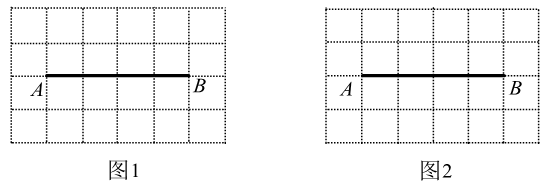(1)、在图1中画出以 $A B$ 为边且周长为无理数的 $▱ A B C D$ ，且点C和点D均在格点上（画出一个即可）.

(2)、在图2中画出以 $A B$ 为对角线的正方形 $A E B F$ ，且点E和点F均在格点上.

查看试题解析
14. 小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α（0°＜α≤90°），得到矩形AB′C′D′，连结BD ．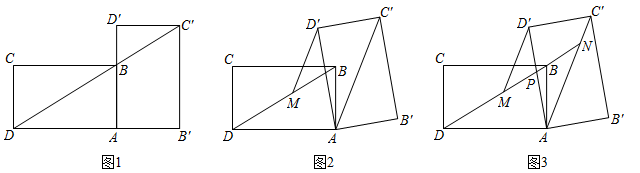

[探究1]如图1，当α＝90°时，点C′恰好在DB延长线上．若AB＝1，求BC的长．

[探究2]如图2，连结AC′，过点D′作D′M∥AC′交BD于点M ．线段D′M与DM相等吗？请说明理由．

[探究3]在探究2的条件下，射线DB分别交AD′，AC′于点P ， N（如图3），发现线段DN ， MN ， PN存在一定的数量关系，请写出这个关系式，并加以证明．

查看试题解析
15. 如图，BD是半径为3的⊙O的一条弦，BD＝4 $\sqrt{2}$ ，点A是⊙O上的一个动点（不与点B，D重合），以A，B，D为顶点作▱ABCD.

(1)、如图2，若点A是劣弧 $\overset{⌢}{B D}$ 的中点.
①求证：▱ABCD是菱形；

②求▱ABCD的面积.

(2)、若点A运动到优弧 $\overset{⌢}{B D}$ 上，且▱ABCD有一边与⊙O相切.
①求AB的长；

②直接写出▱ABCD对角线所夹锐角的正切值.

查看试题解析