浙江省2021年中考数学真题分类汇编05 二次函数

试卷更新日期：2021-06-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
2. 在“探索函数 $y = a x^{2} + b x + c$ 的系数 $a$ ， $b$ ， $c$ 与图象的关系”活动中，老师给出了直角坐标系中的四个点：A（0，2），B（1，0），C（3，1），D（2，3）.同学们探索了经过这四个点中的三个点的二次函数图象，发现这些图象对应的函数表达式各不相同，其中 $a$ 的值最大为（）

A、 $\frac{5}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{6}$ D、 $\frac{1}{2}$

查看试题解析
3. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数，当 $x = m$ 时，函数值分别是 $M_{1}^{}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1}^{} + M_{2} = 0$ ，则称函数 $y_{1}$ 和 $y_{2}$ 具有性质P。以下函数 $y_{1}$ 和 $y_{2}$ 具有性质P的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x - 1$ B、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x + 1$ C、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x - 1$ D、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x + 1$

查看试题解析
4. 已知抛物线 $y = a x^{2} + b x + c$ $(a \neq 0)$ 与 $x$ 轴的交点为A（1，0）和B（3，0），点P₁（ $x_{1}$ ， $y_{1}$ ），P₂（ $x_{2}$ ， $y_{2}$ ）是抛物线上不同于A，B的两个点，记△P₁AB的面积为S₁ ， △P₂AB的面积为S₂。有下列结论：①当 $x_{1} > x_{2} + 2$ 时，S₁>S₂；②当 $x_{1} < 2 - x_{2}$ 时，S₁<S₂；③当 $| x_{1} - 2 | > | x_{2} - 2 | > 1$ 时，S₁>S₂；④当 $| x_{1} - 2 | > | x_{2} + 2 | > 1$ 时，S₁<S₂。其中正确结论的个数是

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

5. 以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt﹣4.9t².现将某弹性小球从地面竖直向上抛出，初速度为v₁ ，经过时间t₁落回地面，运动过程中小球的最大高度为h₁（如图1）；小球落地后，竖直向上弹起，初速度为v₂ ，经过时间t₂落回地面，运动过程中小球的最大高度为h₂（如图2）.若h₁＝2h₂ ，则t₁：t₂＝.

查看试题解析
6. 已知在平面直角坐标系xOy中，点A的坐标为（3，4），M是抛物线 $y = a x^{2} + b x + 2$ （ $a \neq 0$ ）对称轴上的一个动点。小明经探究发现：当 $\frac{b}{a}$ 的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。若抛物线 $y = a x^{2} + b x + 2$ （ $a \neq 0$ ）的对称轴上存在3个不同的点M，使△AOM为直角三角形，则 $\frac{b}{a}$ 的值是

查看试题解析

三、综合题

7. 已知二次函数y＝﹣x²+6x﹣5．

(1)、求二次函数图象的顶点坐标；

(2)、当1≤x≤4时，函数的最大值和最小值分别为多少？

(3)、当t≤x≤t+3时，函数的最大值为m ，最小值为n ，若m﹣n＝3，求t的值．

查看试题解析
8. 已知抛物线 $y = a x^{2} - 2 a x - 8$ $(a \neq 0)$ 经过点 $(- 2 ， 0)$ .

(1)、求抛物线的函数表达式和顶点坐标.

(2)、直线 $l$ 交抛物线于点 $A (- 4 ， m)$ ， $B (n ， 7)$ ， $n$ 为正数.若点 $P$ 在抛物线上且在直线 $l$ 下方（不与点 $A$ ， $B$ 重合），分别求出点 $P$ 横坐标与纵坐标的取值范围，

查看试题解析
9. 如图，二次函数 $y = (x - 1) (x - a)$ （a为常数）的图象的对称轴为直线 $x = 2$ .

(1)、求a的值.

(2)、向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式.

查看试题解析
10. 如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m，在距离D点6米的E处，测得桥面到桥拱的距离EF为1.5m，以桥拱顶点O为原点，桥面为x轴建立平面直角坐标系.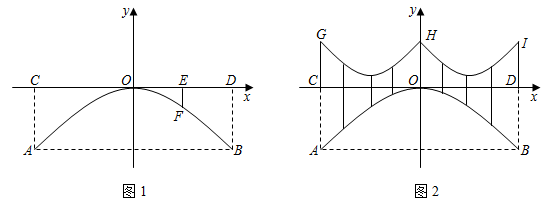

(1)、求桥拱项部O离水面的距离.

(2)、如图2，桥面上方有3根高度均为4m的支柱CG，OH，DI，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.

②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值.

查看试题解析
11. 小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，杯口直径 $A B = 4$ ，且点A，B关于y轴对称，杯脚高 $C O = 4$ ，杯高 $D O = 8$ ，杯底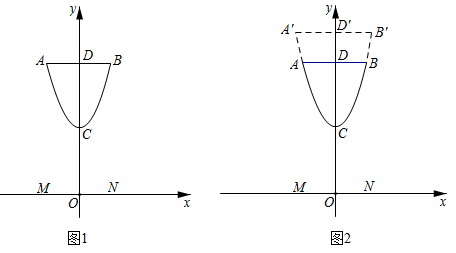MN在x轴上.

(1)、求杯体ACB所在抛物线的函数表达式（不必写出x的取值范围）.

(2)、为使奖杯更加美观，小敏提出了改进方案，如图2，杯体 $A^{'} C B^{'}$ 所在抛物线形状不变，杯口直径 $A^{'} B^{'} / / A B$ ，杯脚高CO不变，杯深 $C D^{'}$ 与杯高 $O D^{'}$ 之比为0.6，求 $A^{'} B^{'}$ 的长.

查看试题解析
12. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为 $y = - \frac{1}{6} {(x - 5)}^{2} + 6$ .

(1)、求雕塑高OA.

(2)、求落水点C，D之间的距离.

(3)、若需要在OD上的点E处竖立雕塑EF， $O E = 10 m$ ， $E F = 1.8 m ， E F ⊥ O D$ .问：顶部F是否会碰到水柱？请通过计算说明.

查看试题解析
13. 如图，已知经过原点的抛物线 $y = 2 x^{2} + m x$ 与x轴交于另一点A（2，0）。

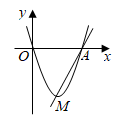(1)、求m的值和抛物线顶点M的坐标；

(2)、求直线AM的解析式。

查看试题解析

14. 今年以来，我市接待的游客人数逐月增加。据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人。

(1)、求四月和五月这两个月中，该景区游客人数平均每月增长百分之几；

(2)、若该景区仅有A，B两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票。

①若丙种门票下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

查看试题解析

15. 在直角坐标系中，设函数 $y = a x^{2} + b x + 1$ （ $a$ ， $b$ 是常数， $a \neq 0$ ）。

(1)、若该函数的图象经过（1，0）和（2，1）两点，求函数的表达式，并写出函数图象的顶点坐标；

(2)、写出一组a、b的值，使函数y=ax²+bx+1的图象与x轴有两个不同的交点，并说明理由.

(3)、已知 $a = b = 1$ ，当 $x = p$ ， $q$ （ $p$ ， $q$ 是实数， $p \neq q$ ）时，该函数对应的函数值分别为P，Q。若 $p + q = 2$ ，求证：P+Q>6 。

查看试题解析