浙江省2021年中考数学真题分类汇编04 一次函数与反比例函数

试卷更新日期：2021-06-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知A，B两地相距60km，甲、乙两人沿同一条公路从A地出发到B地，甲骑自行车匀速行驶3h到达，乙骑摩托车.比甲迟1h出发，行至30km处追上甲，停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地（）

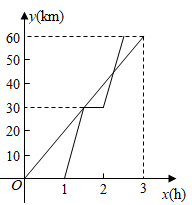A、15km B、16km C、44km D、45km

查看试题解析
2. 已知点P（a ， b）在直线y＝﹣3x﹣4上，且2a﹣5b≤0，则下列不等式一定成立的是（）

A、 $\frac{a}{b}$ ≤ $\frac{5}{2}$ B、 $\frac{a}{b}$ ≥ $\frac{5}{2}$ C、 $\frac{b}{a}$ ≥ $\frac{2}{5}$ D、 $\frac{b}{a}$ ≤ $\frac{2}{5}$

查看试题解析
3. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数，当 $x = m$ 时，函数值分别是 $M_{1}^{}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1}^{} + M_{2} = 0$ ，则称函数 $y_{1}$ 和 $y_{2}$ 具有性质P。以下函数 $y_{1}$ 和 $y_{2}$ 具有性质P的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x - 1$ B、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x + 1$ C、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x - 1$ D、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x + 1$

查看试题解析
4. 如图，点 $A$ ， $B$ 在反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图象上， $A C ⊥ x$ 轴于点 $C$ ， $B D ⊥ x$ 轴于点 $D$ ， $B E ⊥ y$ 轴于点 $E$ ，连结 $A E$ .若 $O E = 1$ ， $O C = \frac{2}{3} O D$ ， $A C = A E$ ，则 $k$ 的值为（）

A、2 B、 $\frac{3 \sqrt{2}}{2}$ C、 $\frac{9}{4}$ D、 $2 \sqrt{2}$

查看试题解析
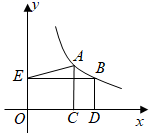5. 如图，正比例函数 $y_{1} = k_{1} x (k_{1} < 0)$ 的图象与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} < 0)$ 的图象相交于A，B两点，点B的横坐标为2，当 $y_{1} > y_{2}$ 时，x的取值范围是（）

A、 $x < - 2$ 或 $x > 2$ B、 $- 2 < x < 0$ 或 $x > 2$ C、 $x < - 2$ 或 $0 < x < 2$ D、 $- 2 < x < 0$ 或 $0 < x < 2$

查看试题解析
6. 已知点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ 在反比例函数 $y = - \frac{12}{x}$ 的图象上.若 $x_{1} < 0 < x_{2}$ ，则（）

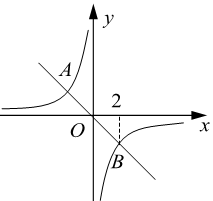A、 $y_{1} < 0 < y_{2}$ B、 $y_{2} < 0 < y_{1}$ C、 $y_{1} < y_{2} < 0$ D、 $y_{2} < y_{1} < 0$

查看试题解析
7. 已知三个点（x₁ ， y₁），（x₂ ， y₂），（x₃ ， y₃）在反比例函数y＝ $\frac{2}{x}$ 的图象上，其中x₁＜x₂＜0＜x₃ ，下列结论中正确的是（）

A、y₂＜y₁＜0＜y₃ B、y₁＜y₂＜0＜y₃ C、y₃＜0＜y₂＜y₁ D、y₃＜0＜y₁＜y₂

查看试题解析

二、填空题

8. 如图，在平面直角坐标系中，有一只用七巧板拼成的“猫”，三角形①的边BC及四边形②的边CD都在x轴上，“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1，则“猫”爪尖F的坐标是.

查看试题解析
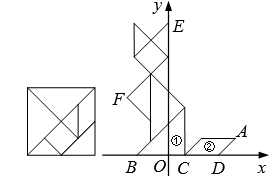9. 如图，在直角坐标系中，△ABC与△ODE是位似图形，则它们位似中心的坐标是．

查看试题解析
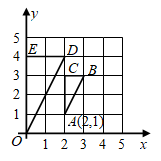10. 将一副三角板如图放置在平面直角坐标系中，顶点A与原点O重合，AB在x轴正半轴上，且 $A B = 4 \sqrt{3}$ ，点E在AD上， $D E = \frac{1}{4} A D$ ，将这副三角板整体向右平移个单位，C，E两点同时落在反比例函数 $y = \frac{k}{x}$ 的图象上.

查看试题解析
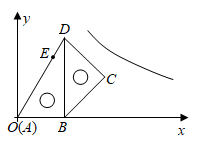11. 在平面直角坐标系中，对于不在坐标轴上的任意一点 $A (x ， y)$ ，我们把点 $B (\frac{1}{x} ， \frac{1}{y})$ 称为点A的“倒数点”.如图，矩形 $O C D E$ 的顶点C为 $(3 ， 0)$ ，顶点E在y轴上，函数 $y = \frac{2}{x} (x > 0)$ 的图象与 $D E$ 交于点A.若点B是点A的“倒数点”，且点B在矩形 $O C D E$ 的一边上，则 $△ O B C$ 的面积为.

查看试题解析
12. 如图，在平面直角坐标系中，正方形ABCD的顶点A在x轴正半轴上，顶点B，C在第一象限，顶点D的坐标 $(\frac{5}{2} ， 2)$ . 反比例函数 $y = \frac{k}{x}$ （常数 $k > 0$ ， $x > 0$ ）的图象恰好经过正方形ABCD的两个顶点，则k的值是.

查看试题解析

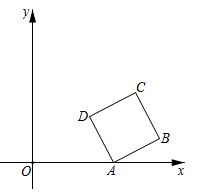
三、综合题

13. 根据数学家凯勒的“百米赛跑数学模型”，前30米称为“加速期”，30米～80米为“中途期”，80米～100米为“冲刺期”．市田径队把运动员小斌某次百米跑训练时速度y（m/s）与路程x（m）之间的观测数据，绘制成曲线如图所示．

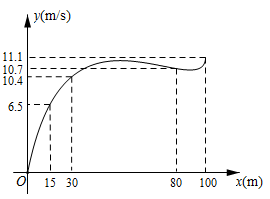(1)、y是关于x的函数吗？为什么？

(2)、“加速期”结束时，小斌的速度为多少？

(3)、根据如图提供的信息，给小斌提一条训练建议．

查看试题解析
14. I号无人机从海拔10m处出发，以10m/min的速度匀速上升，II号无人机从海拔30m处同时出发，以a（m/min）的速度匀速上升，经过5min两架无人机位于同一海拔高度b（m）.无人机海拔高度y（m）与时间x（min）的关系如图.两架无人机都上升了15min.

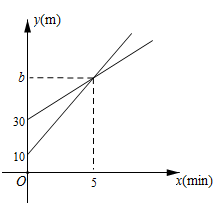(1)、求b的值及II号无人机海拔高度y（m）与时间x（min）的关系式.

(2)、问无人机上升了多少时间，I号无人机比II号无人机高28米.

查看试题解析

15. 某通讯公司就手机流量套餐推出三种方案，如下表：

	A方案	B方案	C方案
每月基本费用（元）	20	56	266
每月免费使用流量（兆）	1024	m	无限
超出后每兆收费（元）	n	n

A，B，C三种方案每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系如图所示.

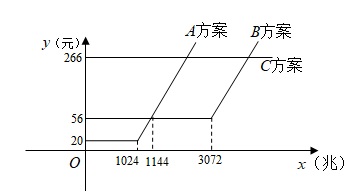(1)、请直接写出m，n的值.

(2)、在A方案中，当每月使用的流量不少于1024兆时，求每月所需的费用y（元）与每月使用的流量x（兆）之间的函数关系式.

(3)、在这三种方案中，当每月使用的流量超过多少兆时，选择C方案最划算？

查看试题解析

16. 电子体重科读数直观又便于携带，为人们带来了方便.某综合实践活动小组设计了简易电子体重秤：制作一个装有踏板（踏板质量忽略不计）的可变电阻R₁ ， R₁与踏板上人的质量m之间的函数关系式为R₁＝km+b（其中k，b为常数，0≤m≤120），其图象如图1所示；图2的电路中，电源电压恒为8伏，定值电阻R₀的阻值为30欧，接通开关，人站上踏板，电压表显示的读数为U₀ ，该读数可以换算为人的质量m，
温馨提示：①导体两端的电压U，导体的电阻R，通过导体的电流I，满足关系式I＝ $\frac{U}{R}$ ；

②串联电路中电流处处相等，各电阻两端的电压之和等于总电压.

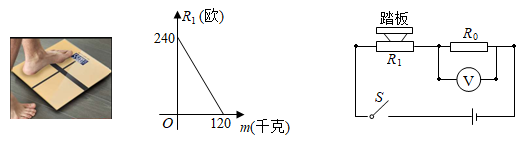(1)、求k，b的值；

(2)、求R₁关于U₀的函数解析式；

(3)、用含U₀的代数式表示m；

(4)、若电压表量程为0~6伏，为保护电压表，请确定该电子体重秤可称的最大质量.

查看试题解析
17. 在直角坐标系中，设函数 $y_{1} = \frac{k_{1}}{x}$ （ $k_{1}$ 是常数， $k_{1} > 0$ ， $x > 0$ ）与函数 $y_{2} = k_{2} x$ （ $k_{2}$ 是常数， $k_{2} \neq 0$ ）的图象交于点A，点A关于 $y$ 轴的对称点为点B。

(1)、若点B的坐标为（-1，2），
①求 $k_{1}$ ， $k_{2}$ 的值； ②当 $y_{1} < y_{2}$ 时，直接写出 $x$ 的取值范围；

(2)、若点B在函数 $y_{3} = \frac{k_{3}}{x}$ （ $k_{3}$ 是常数， $k_{3} \neq 0$ ）的图象上，求 $k_{1} + k_{3}$ 的值。

查看试题解析

18. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克.

营养品信息表
营养成分	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
A包装	1千克	45元
B包装	0.25千克	12元

(1)、问甲、乙两种食材每千克进价分别是多少元？

(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出.若A的数量不低于B的数量，则A为多少包时，每日所获总利润最大？最大总利润为多少元？

查看试题解析

19. 背景：点A在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上， $A B ⊥ x$ 轴于点B， $A C ⊥ y$ 轴于点C，分别在射线 $A C ， B O$ 上取点 $D ， E$ ，使得四边形 $A B E D$ 为正方形.如图1，点A在第一象限内，当 $A C = 4$ 时，小李测得 $C D = 3$ .
探究：通过改变点A的位置，小李发现点D，A的横坐标之间存在函数关系.请帮助小李解决下列问题.

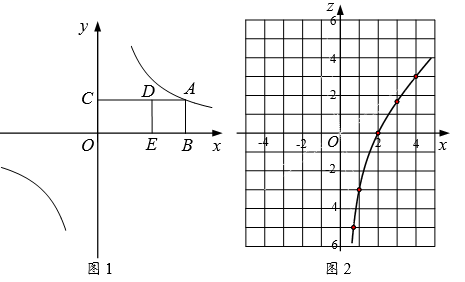(1)、求k的值.

(2)、设点 $A ， D$ 的横坐标分别为 $x ， z$ ，将z关于x的函数称为“Z函数”.如图2，小李画出了 $x > 0$ 时“Z函数”的图象.
①求这个“Z函数”的表达式.

②补画 $x < 0$ 时“Z函数”的图象，并写出这个函数的性质（两条即可）.

③过点 $(3 ， 2)$ 作一直线，与这个“Z函数”图象仅有一个交点，求该交点的横坐标.

查看试题解析
20. 已知在平面直角坐标系xOy中，点A是反比例函数 $y = \frac{1}{x} (x > 0)$ 图像上的一个动点，连结AO，AO的延长线交反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x < 0$ ）的图像于点B，过点A作AE⊥ $y$ 轴于点E。

(1)、如图1，过点B作BF⊥ $x$ 轴于点F，连结EF，
①若 $k = 1$ ，求证：四边形AEFO是平行四边形；

②连结BE，若 $k = 4$ ，求△BOE的面积。

(2)、如图2，过点E作EP∥AB，交反比例函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x < 0$ ）的图像于点P，连结OP。
试探究：对于确定的实数 $k$ ，动点A在运动过程中，△POE的面积是否会发生变化？请说明理由。

查看试题解析