浙江省2021年中考数学真题分类汇编03 方程与不等式

试卷更新日期：2021-06-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 解方程 $- 2 (2 x + 1) = x$ ，以下去括号正确的是（）

A、 $- 4 x + 1 = - x$ B、 $- 4 x + 2 = - x$ C、 $- 4 x - 1 = x$ D、 $- 4 x - 2 = x$

查看试题解析
2. 不等式 $3 x - 1 > 5$ 的解集是（）

A、 $x > 2$ B、 $x < 2$ C、 $x > \frac{4}{3}$ D、 $x < \frac{4}{3}$

查看试题解析
3. 一个不等式的解在数轴上表示如图，则这个不等式可以是（）

A、 $x + 2 > 0$ B、 $x - 2 < 0$ C、 $2 x \geq 4$ D、 $2 - x < 0$

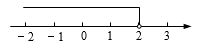查看试题解析
4. 关于x的方程x²﹣4x+m＝0有两个不相等的实数根，则m的取值范围是（）

A、m＞2 B、m＜2 C、m＞4 D、m＜4

查看试题解析
5. 某景点今年四月接待游客25万人次，五月接待游客60.5万人次，设该景点今年四月到五月接待游客人次的增长率为 $x$ （ $x > 0$ ），则（）

A、 $60.5 (1 - x) = 25$ B、 $25 (1 - x) = 60.5$ C、 $60.5 (1 + x) = 25$ D、 $25 (1 + x) = 60.5$

查看试题解析
6. 我国古代数学名著《张邱建算经》中记载：“今有清洒一斗直粟十斗，醑酒一斗直粟三斗.今持粟三斛，得酒五斗，问清、醑酒各几何？”意思是：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清酒、醑酒各几斗？如果设清酒x斗，醑酒y斗，那么可列方程组为（）

A、 ${\begin{array}{l} x + y = 5 \\ 10 x + 3 y = 30 \end{array}$ B、 ${\begin{array}{l} x + y = 5 \\ 3 x + 10 y = 30 \end{array}$ C、 ${\begin{array}{l} x + y = 30 \\ \frac{x}{10} + \frac{y}{3} = 5 \end{array}$ D、 ${\begin{array}{l} x + y = 30 \\ \frac{x}{3} + \frac{y}{10} = 5 \end{array}$

查看试题解析
7. 《九章算术》是中国传统数学的重要著作，书中有一道题“今有五雀六燕，集称之衡，雀俱重，燕俱轻；一雀一燕交而处，衡适平；并燕雀重一斤.问：燕雀一枚，各重几何？”译文：”五只雀、六只燕，共重1斤（占时1斤＝16两）.雀重燕轻，互换其中一只，恰好一样重，问：每只雀、燕重量各为多少？”设雀重x两，燕重y两，可列出方程组（）

A、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$ B、 ${\begin{array}{l} 5 x + 6 y = 10 \\ 4 x + y = 5 y + x \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 10 \\ 5 x + y = 6 y + x \end{array}$ D、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x + y = 6 y + x \end{array}$

查看试题解析
8. 为迎接建党一百周年，某校举行歌唱比赛.901班啦啦队买了两种价格的加油棒助威，其中缤纷棒共花费30元，荧光棒共花费40元，缤纷棒比荧光棒少20根，缤纷棒单价是荧光棒的1.5倍．若设荧光棒的单价为x元，根据题意可列方程为（）

A、 $\frac{40}{1.5 x}$ ﹣ $\frac{30}{x}$ ＝20 B、 $\frac{40}{x}$ ﹣ $\frac{30}{1.5 x}$ ＝20 C、 $\frac{30}{x}$ ﹣ $\frac{40}{1.5 x}$ ＝20 D、 $\frac{30}{1.5 x}$ ﹣ $\frac{40}{x}$ ＝20

查看试题解析

二、填空题

9. 不等式 $2 (y + 1) < y + 3$ 的解为.

查看试题解析
10. 已知二元一次方程x+3y＝14，请写出该方程的一组整数解．

查看试题解析
11. 我国明代数学读本《算法统宗》有一道题，其题意为：客人一起分银子，若每人7两，还剩4两；若每人9两，则差8两，银子共有两.（注：明代时1斤=16两）

查看试题解析
12. 已知 ${\begin{matrix} x = 2 \\ y = m \end{matrix}$ 是方程 $3 x + 2 y = 10$ 的一个解，则m的值是.

查看试题解析
13. 不等式组 ${\begin{array}{l} x - 3 < 4 \\ \frac{3 x + 2}{4} \geq 1 \end{array}$ 的解为.

查看试题解析

三、计算题

14. 解分式方程： $\frac{2 x - 1}{x + 3} = 1$

查看试题解析
15.

(1)、计算： $(1 + a) (1 - a) + {(a + 3)}^{2}$ .

(2)、解不等式组： ${\begin{array}{l} 2 x + 1 < 9 ① \\ 3 - x \leq 0 ② \end{array}$ .

查看试题解析
16. 解方程组： ${\begin{matrix} 2 x + y = 4 \\ x - y = - 1 \end{matrix}$ .

查看试题解析
17.

(1)、计算： $4 \sin 60 ° - \sqrt{12} + {(2 - \sqrt{3})}^{0}$ .

(2)、解不等式： $5 x + 3 ⩾ 2 (x + 3)$ .

查看试题解析

四、解答题

18. 小敏与小霞两位同学解方程3（x﹣3）＝（x﹣3）²的过程如下框：

小敏：

两边同除以（x﹣3），得

3＝x﹣3，

则x＝6．

小霞：

移项，得3（x﹣3）﹣（x﹣3）²＝0，

提取公因式，得（x﹣3）（3﹣x﹣3）＝0．

则x﹣3＝0或3﹣x﹣3＝0，

解得x₁＝3，x₂＝0．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．

查看试题解析

19. 以下是圆圆解不等式组 ${\begin{matrix} 2 (1 + x) > - 1 ① \\ - (1 - x) > - 2 ② \end{matrix}$
的解答过程：

解：由①，得 $2 + x > - 1$ ，所以 $x > - 3$

由②，得 $1 - x > 2$ ，所以 $- x > 1$ ，所以 $x > - 1$

所以原不等式组的解是 $x > - 1$ 。

圆圆的解答过程是否有错误？如果有错误，请写出正确的解答过程。

查看试题解析

20. 今年以来，我市接待的游客人数逐月增加。据统计，游玩某景区的游客人数三月份为4万人，五月份为5.76万人。

(1)、求四月和五月这两个月中，该景区游客人数平均每月增长百分之几；

(2)、若该景区仅有A，B两个景点，售票处出示的三种购票方式如下表所示：

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人

据预测，六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万，并且当甲、乙两种门票价格不变时，丙种门票每下降1元，将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票。

①若丙种门票下降10元，求景区六月份的门票总收入；

②问：将丙种门票价格下降多少元时，景区六月份的门票总收入有最大值？最大值是多少万元？

查看试题解析

21. 某公司生产的一种营养品信息如下表.已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克.

营养品信息表
营养成分	每千克含铁42毫克
配料表	原料	每千克含铁
	甲食材	50毫克
	乙食材	10毫克
规格	每包食材含量	每包单价
A包装	1千克	45元
B包装	0.25千克	12元

(1)、问甲、乙两种食材每千克进价分别是多少元？

(2)、该公司每日用18000元购进甲、乙两种食材并恰好全部用完.

①问每日购进甲、乙两种食材各多少千克？

②已知每日其他费用为2000元，且生产的营养品当日全部售出.若A的数量不低于B的数量，则A为多少包时，每日所获总利润最大？最大总利润为多少元？

查看试题解析