初中数学浙教版九年级上册1.2 二次函数的图象 同步练习
试卷更新日期:2021-06-29 类型:同步测试
一、单选题
-
1. 抛物线y=﹣x2经过平移得到抛物线y=﹣(x+2)2﹣3,平移的方法是( )A、向左平移2个,再向下平移3个单位 B、向右平移2个,再向下平移3个单位 C、向左平移2个,再向上平移3个单位 D、向右平移2个,再向上平移3个单位2. 抛物线y=﹣3(x+1)2﹣2的顶点坐标是( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)3. 抛物线 的顶点坐标为( )A、(3,-5) B、(-3,5) C、(-3,-5) D、(3,5)4. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
 A、 B、 C、 D、5. 将二次函数 的图象向左平移1个单位长度,再向上平移2个单位后,所得图象的函数解析式是( )A、 B、 C、 D、6. 将抛物线y=x2﹣4x+3平移,使它平移后图象的顶点为(﹣2,4),则需将该抛物线( )A、先向右平移4个单位,再向上平移5个单位 B、先向右平移4个单位,再向下平移5个单位 C、先向左平移4个单位,再向上平移5个单位 D、先向左平移4个单位,再向下平移5个单位7. 如图,抛物线y=a +bx+c与直线y=kx交于M , N两点,则二次函数y=a +(b﹣k)x+c的图象可能是( )
A、 B、 C、 D、5. 将二次函数 的图象向左平移1个单位长度,再向上平移2个单位后,所得图象的函数解析式是( )A、 B、 C、 D、6. 将抛物线y=x2﹣4x+3平移,使它平移后图象的顶点为(﹣2,4),则需将该抛物线( )A、先向右平移4个单位,再向上平移5个单位 B、先向右平移4个单位,再向下平移5个单位 C、先向左平移4个单位,再向上平移5个单位 D、先向左平移4个单位,再向下平移5个单位7. 如图,抛物线y=a +bx+c与直线y=kx交于M , N两点,则二次函数y=a +(b﹣k)x+c的图象可能是( ) A、
A、 B、
B、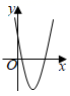 C、
C、 D、
D、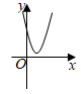 8. 函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(﹣1,n),其中n>0.以下结论正确的是( )
8. 函数y=ax2+bx+c(a≠0)的图象与x轴交于点(2,0),顶点坐标为(﹣1,n),其中n>0.以下结论正确的是( )①abc>0;②函数y=ax2+bx+c(a≠0)在x=1和x=﹣2处的函数值相等;③函数y=kx+1的图象与y=ax2+bx+c(a≠0)的函数图象总有两个不同交点;④函数y=ax2+bx+c(a≠0)在﹣3≤x≤3内既有最大值又有最小值.
A、①③ B、①②③ C、①④ D、②③④9. 在同一平面直角坐标系中,若抛物线y=mx2+2x﹣n与y=﹣6x2﹣2x+m﹣n关于x轴对称,则m,n的值为( )A、m=﹣6,n=﹣3 B、m=﹣6,n=3 C、m=6,n=﹣3 D、m=6,n=310. 已知二次函数y=ax2+bx+c,其中a<0,若函数图象与x轴的两个交点均在负半轴,则下列判断错误的是( )A、abc<0 B、b>0 C、c<0 D、b+c<0二、填空题
-
11. 二次函数 图象的对称轴是 .12. 抛物线 的开口方向为向13. 抛物线 的顶点坐标是 .14. 将抛物线 向上平移3个单位长度后,经过点 ,则8a-4b-11的值是 .15. 如果抛物线y=ax2+bx+c在对称轴左侧呈上升趋势,那么a的取值范围是 .
三、计算题
