湖北省荆州市2021年中考数学试卷
试卷更新日期:2021-06-29 类型:中考真卷
一、单选题
-
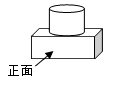
1. 在实数 ,0, , 中,无理数是( )A、 B、0 C、 D、2. 如图是由一个圆柱和一个长方体组成的几何体,则该几何体的俯视图是( )
 A、
A、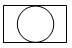 B、
B、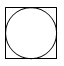 C、
C、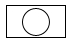 D、
D、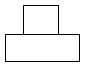 3. 若等式 +( )= 成立,则括号中填写单项式可以是( )A、a B、 C、 D、4. 阅读下列材料,其①~④步中数学依据错误的是( )
3. 若等式 +( )= 成立,则括号中填写单项式可以是( )A、a B、 C、 D、4. 阅读下列材料,其①~④步中数学依据错误的是( )如图:已知直线 , ,求证: .
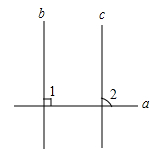
证明:①∵ (已知)
∴ (垂直的定义)
②又∵ (已知)
③∴ (同位角相等,两直线平行)
∴ (等量代换)
④∴ (垂直的定义).
A、① B、② C、③ D、④5. 若点 关干x轴的对称点在第四象限,则a的取值范围在数轴上表示为( )A、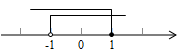 B、
B、 C、
C、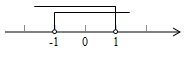 D、
D、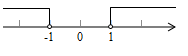 6. 已知:如图,直线 与双曲线 在第一象限交于点 ,与x轴、y轴分别交于A,B两点,则下列结论错误的是( )
6. 已知:如图,直线 与双曲线 在第一象限交于点 ,与x轴、y轴分别交于A,B两点,则下列结论错误的是( )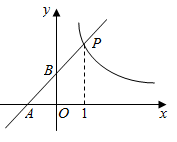 A、 B、 是等腰直角三角形 C、 D、当 时,7. 如图,矩形 的边 , 分别在x轴、y轴的正半轴上,点D在 的延长线上.若 , ,以O为圆心、 长为半径的弧经过点B,交y轴正半轴于点E,连接 , 、则 的度数是( )
A、 B、 是等腰直角三角形 C、 D、当 时,7. 如图,矩形 的边 , 分别在x轴、y轴的正半轴上,点D在 的延长线上.若 , ,以O为圆心、 长为半径的弧经过点B,交y轴正半轴于点E,连接 , 、则 的度数是( )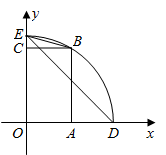 A、 B、 C、 D、8. 如图,在 中, , ,点D,P分别是图中所作直线和射线与 , 的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )
A、 B、 C、 D、8. 如图,在 中, , ,点D,P分别是图中所作直线和射线与 , 的交点.根据图中尺规作图痕迹推断,以下结论错误的是( )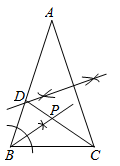 A、 B、 C、 D、9. 如图,在菱形 中, , ,以B为圆心、 长为半径画 ,点P为菱形内一点,连接 , , .当 为等腰直角三角形时,图中阴影部分的面积为( )
A、 B、 C、 D、9. 如图,在菱形 中, , ,以B为圆心、 长为半径画 ,点P为菱形内一点,连接 , , .当 为等腰直角三角形时,图中阴影部分的面积为( )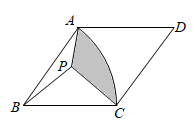 A、 B、 C、 D、10. 定义新运算“※”:对于实数m,n,p,q,有 ,其中等式右边是通常的加法和乘法运算,如: .若关于x的方程 有两个实数根,则k的取值范围是( )A、 且 B、 C、 且 D、
A、 B、 C、 D、10. 定义新运算“※”:对于实数m,n,p,q,有 ,其中等式右边是通常的加法和乘法运算,如: .若关于x的方程 有两个实数根,则k的取值范围是( )A、 且 B、 C、 且 D、二、填空题
-
11. 已知: , ,则 .12. 有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁,现在任意取出一把钥匙去开任意一把锁,一次就能打开锁的概率是 .13. 如图, 是 的直径, 是 的弦, 于D,连接 ,过点D作 交 于F,过点B的切线交 的延长线于E.若 , ,则 .
 14. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )
14. 如图1是一台手机支架,图2是其侧面示意图, , 可分别绕点A,B转动,测量知 , .当 , 转动到 , 时,点C到 的距离为cm.(结果保留小数点后一位,参考数据: , )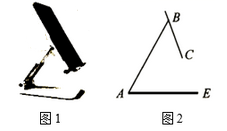 15. 若关于x的方程 的解是正数,则m的取值范围为.16. 如图,过反比例函数 图象上的四点 , , , 分别作x轴的垂线,垂足分别为 , , , ,再过 , , , 分别作y轴, , , 的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为 , , , , ,则 与 的数量关系为.
15. 若关于x的方程 的解是正数,则m的取值范围为.16. 如图,过反比例函数 图象上的四点 , , , 分别作x轴的垂线,垂足分别为 , , , ,再过 , , , 分别作y轴, , , 的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为 , , , , ,则 与 的数量关系为.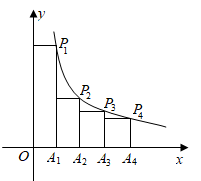
三、解答题
-
17. 先化简,再求值: ,其中 .18. 已知:a是不等式 的最小整数解,请用配方法解关于x的方程 .19. 如图,在 的正方形网格图形中小正方形的边长都为1,线段 与 的端点都在网格小正方形的顶点(称为格点)上.请在网格图形中画图:
 (1)、以线段 为一边画正方形 ,再以线段 为斜边画等腰直角三角形 ,其中顶点F在正方形 外;(2)、在(1)中所画图形基础上,以点B为其中一个顶点画一个新正方形,使新正方形的面积为正方形 和 面积之和,其它顶点也在格点上.20. 高尔基说:“书,是人类进步的阶梯.”阅读可以启智增慧,拓展视野,……为了解学生寒假阅读情况.开学初学校进行了问卷调查,并对部分学生假期(24天)的阅读总时间作了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为t(小时),阅读总时间分为四个类别: , , , ,将分类结果制成如下两幅统计图(尚不完整).
(1)、以线段 为一边画正方形 ,再以线段 为斜边画等腰直角三角形 ,其中顶点F在正方形 外;(2)、在(1)中所画图形基础上,以点B为其中一个顶点画一个新正方形,使新正方形的面积为正方形 和 面积之和,其它顶点也在格点上.20. 高尔基说:“书,是人类进步的阶梯.”阅读可以启智增慧,拓展视野,……为了解学生寒假阅读情况.开学初学校进行了问卷调查,并对部分学生假期(24天)的阅读总时间作了随机抽样分析.设被抽样的每位同学寒假阅读的总时间为t(小时),阅读总时间分为四个类别: , , , ,将分类结果制成如下两幅统计图(尚不完整).
根据以上信息,回答下列问题:
(1)、本次抽样的样本容量为;(2)、补全条形统计图;(3)、扇形统计图中a的值为 , 圆心角 的度数为;(4)、若该校有2000名学生,估计寒假阅读的总时间少于24小时的学生有多少名?对这些学生用一句话提一条阅读方面的建议.21. 小爱同学学习二次函数后,对函数 进行了探究,在经历列表、描点、连线步骤后,得到加下的函数图象.请根据函数图象,回答下列问题: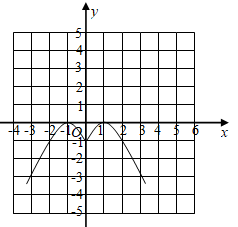 (1)、观察探究:
(1)、观察探究:①写出该函数的一条性质:;
②方程 的解为:;
③若方程 有四个实数根,则a的取值范围是.
(2)、延伸思考:将函数 的图象经过怎样的平移可得到函数 的图象?写出平移过程,并直接写出当 时,自变量x的取值范围.
22. 小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.(1)、求买一支康乃馨和一支百合各需多少元?(2)、小美准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为w元,康乃馨有x支,求w与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.23. 在矩形 中, , ,F是对角线 上不与点A,C重合的一点,过F作 于E,将 沿 翻折得到 ,点G在射线 上,连接 .(1)、如图1,若点A的对称点G落在 上, ,延长 交 于H,连接 .
①求证: ;
②求 .
(2)、如图2,若点A的对称点G落在 延长线上, ,判断 与 是否全等,并说明理由. 24. 已知:直线 与x轴、y轴分别交于A、B两点,点C为直线 上一动点,连接 , 为锐角,在 上方以 为边作正方形 ,连接 ,设 .
24. 已知:直线 与x轴、y轴分别交于A、B两点,点C为直线 上一动点,连接 , 为锐角,在 上方以 为边作正方形 ,连接 ,设 .

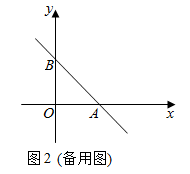 (1)、如图1,当点C在线段 上时,判断 与 的位置关系,并说明理由;(2)、真接写出点E的坐标(用含t的式子表示);(3)、若 ,经过点A的抛物线 顶点为P,且有 , 的面积为 .当 时,求抛物线的解析式.
(1)、如图1,当点C在线段 上时,判断 与 的位置关系,并说明理由;(2)、真接写出点E的坐标(用含t的式子表示);(3)、若 ,经过点A的抛物线 顶点为P,且有 , 的面积为 .当 时,求抛物线的解析式.