湖北省鄂州市2021年中考数学试卷
试卷更新日期:2021-06-29 类型:中考真卷
一、单选题
-
1. 实数6的相反数等于( )A、 B、6 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. “国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列四个几何体中,主视图是三角形的是( )A、
4. 下列四个几何体中,主视图是三角形的是( )A、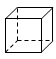 B、
B、 C、
C、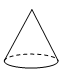 D、
D、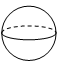 5. 已知锐角 ,如图,按下列步骤作图:①在 边取一点D,以O为圆心, 长为半径画 ,交 于点C,连接 .②以D为圆心, 长为半径画 ,交 于点E,连接 .则 的度数为( )
5. 已知锐角 ,如图,按下列步骤作图:①在 边取一点D,以O为圆心, 长为半径画 ,交 于点C,连接 .②以D为圆心, 长为半径画 ,交 于点E,连接 .则 的度数为( )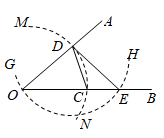 A、 B、 C、 D、6. 已知 为实数﹐规定运算: , , , ,……, .按上述方法计算:当 时, 的值等于( )A、 B、 C、 D、7. 数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于x的不等式 的解集是( )
A、 B、 C、 D、6. 已知 为实数﹐规定运算: , , , ,……, .按上述方法计算:当 时, 的值等于( )A、 B、 C、 D、7. 数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于x的不等式 的解集是( ) A、 B、 C、 D、8. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )
A、 B、 C、 D、8. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )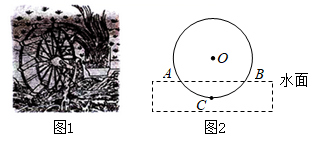 A、1米 B、 米 C、2米 D、 米9. 二次函数 的图象的一部分如图所示.已知图象经过点 ,其对称轴为直线 .下列结论:① ;② ;③ ;④若抛物线经过点 ,则关于x的一元二次方程 的两根分别为-3,5,上述结论中正确结论的个数为( )
A、1米 B、 米 C、2米 D、 米9. 二次函数 的图象的一部分如图所示.已知图象经过点 ,其对称轴为直线 .下列结论:① ;② ;③ ;④若抛物线经过点 ,则关于x的一元二次方程 的两根分别为-3,5,上述结论中正确结论的个数为( )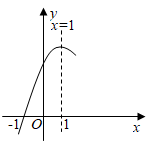 A、1个 B、2个 C、3个 D、4个10. 如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是( )
A、1个 B、2个 C、3个 D、4个10. 如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是( ) A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. 计算:= .12. “最美鄂州,从我做起”.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动.6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是.13. 已知实数a、b满足 ,若关于x的一元二次方程 的两个实数根分别为 、 ,则 .14. 如图,在平面直角坐标系中,点C的坐标为 ,点A的坐标为 ,将点A绕点C顺时针旋转 得到点B,则点B的坐标为.
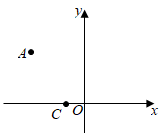 15. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.
15. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.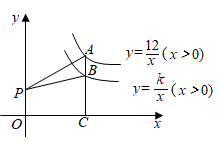 16. 如图,四边形 中, , , 于点D.若 , ,则线段 的长为.
16. 如图,四边形 中, , , 于点D.若 , ,则线段 的长为.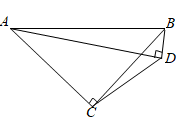
三、解答题
-
17. 先化简,再求值: ,其中 .18. 为了引导青少年学党史、颂党恩、跟党走,某中学举行了“南献礼建党百年”党史知识竞赛活动.胡老师从全校学生的答卷中随机地抽取了部分学生的答卷进行了统计分析(卷面满分100分,且得分x均为不小于60的整数)﹐并将竞赛成绩划分为四个等级:基本合格( ).合格( )、良好( )、优秀( ),制作了如下统计图(部分信息未给出):

根据图中提供的信息解决下列问题:
(1)、胡老师共抽取了 名学生的成绩进行统计分析,扇形统计图中“基本合格”等级对应的扇形圆心角度数为 ﹐请补全条形统计图.
(2)、现从“优秀”等级的甲、乙、丙、丁四名学生中任选两人参加全市党史知识竞赛活动,请用画树形图的方法求甲学生被选到的概率.19. 如图,在 中,点E、F分别在边 、 上,且 .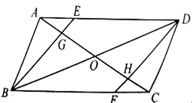 (1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.20. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
(1)、探究四边形 的形状,并说明理由;(2)、连接 ,分别交 、 于点G、H,连接 交 于点O.若 , ,求 的长.20. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.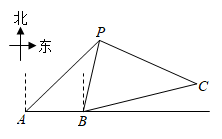 (1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)21. 为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, ;当 时, .(1)、求y与x之间的函数关系式(不求自变量的取值范围);(2)、受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)22. 如图,在 中, ,O为 边上一点,以O为圆心, 长为半径的 与 边相切于点D,交 于点E.
(1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)21. 为了实施乡村振兴战略,帮助农民增加收入,市政府大力扶持农户发展种植业,每亩土地每年发放种植补贴120元.张远村老张计划明年承租部分土地种植某种经济作物.考虑各种因素,预计明年每亩土地种植该作物的成本y(元)与种植面积x(亩)之间满足一次函数关系,且当 时, ;当 时, .(1)、求y与x之间的函数关系式(不求自变量的取值范围);(2)、受区域位置的限制,老张承租土地的面积不得超过240亩.若老张明年销售该作物每亩的销售额能达到2160元,当种植面积为多少时,老张明年种植该作物的总利润最大?最大利润是多少?(每亩种植利润=每亩销售额-每亩种植成本+每亩种植补贴)22. 如图,在 中, ,O为 边上一点,以O为圆心, 长为半径的 与 边相切于点D,交 于点E. (1)、求证: ;(2)、连接 ,若 , ,求线段 的长.23. 数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.
(1)、求证: ;(2)、连接 ,若 , ,求线段 的长.23. 数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.猜想发现:由 ; ; ; ; ;
猜想:如果 , ,那么存在 (当且仅当 时等号成立).
猜想证明:∵
∴①当且仅当 ,即 时, ,∴ ;
②当 ,即 时, ,∴ .
综合上述可得:若 , ,则 成立(当日仅当 时等号成立).
(1)、猜想运用:对于函数 ,当x取何值时,函数y的值最小?最小值是多少?(2)、变式探究:对于函数 ,当x取何值时,函数y的值最小?最小值是多少?(3)、拓展应用:(3)疫情期间、为了解决疑似人员的临隔离问题.高速公路榆测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图.设每间离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大?最大面积是多少?
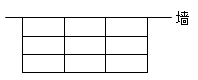 24. 如图,直线 与x轴交于点B,与y轴交于点A,点P为线段 的中点,点Q是线段 上一动点(不与点O、A重合).
24. 如图,直线 与x轴交于点B,与y轴交于点A,点P为线段 的中点,点Q是线段 上一动点(不与点O、A重合). (1)、请直接写出点A、点B、点P的坐标;(2)、连接 ,在第一象限内将 沿 翻折得到 ,点O的对应点为点E.若 ,求线段 的长;(3)、在(2)的条件下,设抛物线 的顶点为点C.
(1)、请直接写出点A、点B、点P的坐标;(2)、连接 ,在第一象限内将 沿 翻折得到 ,点O的对应点为点E.若 ,求线段 的长;(3)、在(2)的条件下,设抛物线 的顶点为点C.①若点C在 内部(不包括边),求a的取值范围;
②在平面直角坐标系内是否存在点C,使 最大?若存在,请直接写出点C的坐标;若不存在,请说明理由.