上海市嘉定区2021年中考数学二模试卷

试卷更新日期：2021-06-29 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，一定是无理数的是（）

A、 $\frac{22}{7}$ B、 $- π$ C、 $\sqrt[3]{27}$ D、0.345345…（它的位数无限）

查看试题解析
2. 化简 ${(3 a^{3})}^{2}$ 的结果是（）

A、 $6 a^{6}$ B、 $9 a^{9}$ C、 $6 a^{9}$ D、 $9 a^{6}$

查看试题解析
3. 如果一次函数 $y = k x + b$ 的图像经过第二、三象限，且与y轴的负半轴相交，那么在下列四个正确的选项是（）

A、 $k < 0$ ， $b < 0$ B、 $k > 0$ ， $b > 0$ C、 $k < 0$ ， $b > 0$ D、 $k > 0$ ， $b < 0$

查看试题解析
4. 已知两组数据： $x_{1}$ ， $x_{2}$ ， $x_{3}$ 和 $x_{1} + 2$ ， $x_{2} + 2$ ， $x_{3} + 2$ ，下列说法正确的是（）

A、平均数相等，方差不相等 B、中位数相等，方差不相等 C、平均数不相等，方差相等 D、中位数不相等，众数相等

查看试题解析
5. 下列命题：①等腰梯形的两个底角相等；②两个底角相等的梯形是等腰梯形；③等腰梯形的对角线等；⑤对角线相等的梯形是等腰梯形，其中真命题的个数是（）

A、0 B、2 C、3 D、4

查看试题解析
6. 已知点 $A (4 ， 0)$ ， $B (0 ， 3)$ ，如果⊙A的半径为2，⊙B的半径为7，那么⊙A与⊙B的位置关系（）

A、内切 B、外切 C、内含 D、外离

查看试题解析

二、填空题

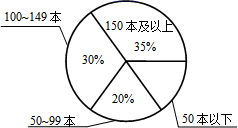
7. 2021年5月，国家统计局发布了第七次全国人口统计数据：全国共有人口141178万，用科学记数法表示141178万人，那么可以表示为万人．（保留两个有效数字）

查看试题解析
8. 函数 $y = \sqrt{2 - 3 x}$ 的定义域是．

查看试题解析
9. 因式分解： $x^{2} y - 4 y$ = ．

查看试题解析
10. 不等式组 ${\begin{array}{l} x - 2 < 0 \\ 2 x + 1 \geq 0 \end{array}$ 的解集是．

查看试题解析
11. 方程 $\sqrt{x^{2} - 9} = 4$ 的解是

查看试题解析
12. 如果关于x的方程 $2 x^{2} - 3 x + k = 0$ 有两个相等的实数根，那么常数k的值为．

查看试题解析
13. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像与正比例函数 $y = k x (k \neq 0)$ 的图像有两个交点，其中一个交点的横坐标为1，另外一个交点的纵坐标为 $- 3$ ，那么常数k的值是．

查看试题解析
14. 某校对部分学生家庭进行图书量调查，调查情况如图所示，如果本次调查中，有50本以下图书的学生家庭有24户，那么参加本次调查的学生家庭数有户．

查看试题解析
15. 在物理实验课上，同学们用三个开关，两个灯泡、一个电源及若干条导线连接成如图所示的电路图，随机闭合图中的两个开关，有一个灯泡发光的概率是．

查看试题解析
16. 如图， $△ A B C$ 中，D为边AC的中点，设向量 $\vec{B D} = \vec{a}$ ，向量 $\vec{B C} = \vec{b}$ ，那么向量 $\vec{C A}$ 用向量 $\vec{a}$ ， $\vec{b}$ 可表示为．

查看试题解析
17. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射，如果被b反射出的光线n与光线m平行，且 $∠ 1 = 37 °$ ，那么 $∠ 2$ 的度数为．

查看试题解析
18. 如图所示，诗的意思是：有正方形的城池一座，四面城墙的正中有门，从南门口（点D）直行8里有一塔（点A），自西门（点E）直行2里至点B，切城角（点C）也可以看见塔，问这座方城每面城墙的长是里．

查看试题解析

三、解答题

19. 清朝《数理精蕴》里有一首小诗《古色古香方城池》：今有一座古方城，四面正中都开门，南门直行八里止，脚下有座塔耸立．又出西门二里停，切城角恰见塔形，请问诸君能算者，方城每边长是几？
如图所示，诗的意思是：有正方形的城池一座，四面城墙的正中有门，从南门口（点D）直行8里有一塔（点A），自西门（点E）直行2里至点B，切城角（点C）也可以看见塔，问这座方城每面城墙的长是多少里？

查看试题解析
20. 计算： ${(\frac{1}{4})}^{- 1} + 2 \cos 45 ° - | - \sqrt{2} | + {(2021 - π)}^{0}$ ．

查看试题解析
21. 解分式方程： $\frac{x + 2}{x - 2} - \frac{16}{x^{2} - 4} = \frac{1}{x + 2}$ ．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $\sin ∠ A = \frac{3}{5}$ ， $A B = 5$ ，BD平分 $∠ A B C$ ．

(1)、求BC的长；

(2)、求 $∠ C B D$ 的正切值．

查看试题解析
23. 某小区外面的一段长120米的街道上要开辟停车位，计划每个停车位都是同样的长方形且每个长方形的宽均为2.2米，如果长方形的较长的边与路段的边平行，如图1所示，那么恰好能够停放24辆车．（备注： $\sqrt{2} = 1.414$ ， $\sqrt{3} = 1.732$ ， $\sqrt{5} = 2.236$ ）

(1)、如果长方形的边与街道的边缘成45°角，那么按图1，图2中的方法停放，一个停车位占用街道的长度各是多少？（结果保留一位小数）

(2)、如果按照图2中的方法停放车辆，这段路上最多可以停放多少车辆？

查看试题解析
24. 已知四边形ABCD是菱形（如图），以点B为圆心，BD长为半径的圆分别与边AD、CD、BC、AB，相交于点E、F、G、H，联结BE．

(1)、求证： $△ B D E ~ △ A D B$ ；

(2)、联结EG，如果 $E G / / A B$ ，求证： $A E^{2} = D E \cdot C B$ ．

查看试题解析
25. 在平面直角坐标系xOy中（如图），抛物线 $y = a x^{2} + b x + a - 4 (a > 0)$ 的对称轴是直线 $x = 1$ ．

(1)、求抛物线 $y = a x^{2} + b x + a - 4 (a > 0)$ 的顶点坐标；

(2)、当x满足 $- 2 \leq x \leq 3$ 时，函数值y满足 $- 4 \leq y \leq 5$ ，试求a的值；

(3)、将抛物线 $y = a x^{2} + b x + a - 4 (a > 0)$ 与x轴所围成的区域（不包含边界）记为G，将横坐标、纵坐标都是整数的点称为“整点”，如果区域G内恰好只有5个“整点”，结合函数的图象，求a的取值范围．

查看试题解析
26. 已知点P为线段AB上的一点，将线段AP绕点A逆时针旋转60°，得到线段AC；再将线段绕点B逆时针旋转120°，得到线段BD；点M是AD的中点，联结BM、CM．

(1)、如图1，如果点P在线段CM上，求证： $P M / / B D$ ；

(2)、如图1，如果点P在线段CM上，求证： $P C = 2 P M$ ；

(3)、如果点P不在线段CM上（如图12），当点P在线段AB上运动时， $∠ B C M$ 的正切值是否发生变化？如果发生变化，简述理由；如果不发生变化，请求出 $∠ B C M$ 的正切值．

查看试题解析