山东省枣庄市台儿庄区2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. 下列各式中正确的是( )A、 B、 C、 D、2. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )A、众数是36.5 B、中位数是36.7 C、平均数是36.6 D、方差是0.44. 现有4条线段,长度依次是2、4、6、7,从中任选三条,能组成三角形的概率是( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )
3. 某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )A、众数是36.5 B、中位数是36.7 C、平均数是36.6 D、方差是0.44. 现有4条线段,长度依次是2、4、6、7,从中任选三条,能组成三角形的概率是( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,CD为中线,延长CB至点E,使BE=BC,连结DE,F为DE中点,连结BF.若AC=8,BC=6,则BF的长为( )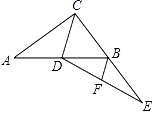 A、2 B、2.5 C、3 D、46. 已知光速为300000千米秒,光经过t秒( )传播的距离用科学记数法表示为 千米,则n可能为( )A、5 B、6 C、5或6 D、5或6或77. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )
A、2 B、2.5 C、3 D、46. 已知光速为300000千米秒,光经过t秒( )传播的距离用科学记数法表示为 千米,则n可能为( )A、5 B、6 C、5或6 D、5或6或77. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )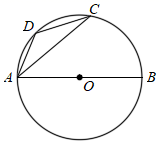 A、110° B、130° C、140° D、160°8. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、9. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( )
A、110° B、130° C、140° D、160°8. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、9. 如图,矩形 的顶点 在反比例函数 的图象上,点 和点 在 边上, ,连接 轴,则 的值为( ) A、 B、3 C、4 D、10. 已知二次函数 图象的对称轴为 ,其图象如图所示,现有下列结论:① ;② ;③ ;④ ;⑤ .正确的是( )
A、 B、3 C、4 D、10. 已知二次函数 图象的对称轴为 ,其图象如图所示,现有下列结论:① ;② ;③ ;④ ;⑤ .正确的是( )
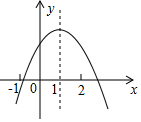 A、①③ B、②⑤ C、③④ D、④⑤11. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )
A、①③ B、②⑤ C、③④ D、④⑤11. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )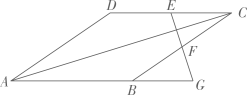 A、13 B、10 C、12 D、512. 如图,在 中, , 是 的中点,过点 作 的平行线,交 于点E,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为( )
A、13 B、10 C、12 D、512. 如图,在 中, , 是 的中点,过点 作 的平行线,交 于点E,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为( )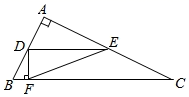 A、 B、5 C、 D、10
A、 B、5 C、 D、10二、填空题
-
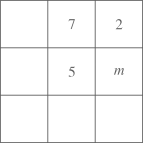
13. 已知 , .若 ,则 的值为 .14. 幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为.
 15. 两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为.16. 如图,直线 与x轴、y轴分别交于A、B两点,把 绕点B逆时针旋转90°后得到 ,则点 的坐标是.
15. 两组数据:3,a,b,5与a,4,2b的平均数都是3.若将这两组数据合并为一组新数据,则这组新数据的众数为.16. 如图,直线 与x轴、y轴分别交于A、B两点,把 绕点B逆时针旋转90°后得到 ,则点 的坐标是.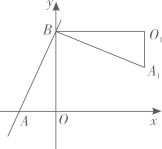 17. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.
17. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.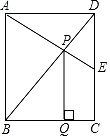 18. 下面各图形是由大小相同的黑点组成,图1中有2个点,图2中有7个点,图3中有14个点,……,按此规律,第10个图中黑点的个数是 .
18. 下面各图形是由大小相同的黑点组成,图1中有2个点,图2中有7个点,图3中有14个点,……,按此规律,第10个图中黑点的个数是 .
三、解答题
-
19. 先化简,再求值: ,其中 .20. 我们知道,任意一个正整数 都可以进行这样的分解: ( , 是正整数,且 ),在 的所有这种分解中,如果 , 两因数之差的绝对值最小,我们就称 是 的最佳分解.并规定: .
例如:18可以分解成 , 或 ,因为 ,所以 是18的最佳分解,所以 .
(1)、填空: ; .(2)、一个两位正整数t( , ,a , b为正整数),交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54,求出所有的两位正整数;并求 的最大值;(3)、填空:① ;
② ;
21. 如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.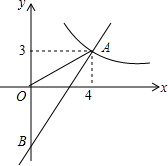 (1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.22. 在等腰△ABC中,AB=BC , 点D , E在射线BA上,BD=DE , 过点E作EF∥BC , 交射线CA于点F . 请解答下列问题:
(1)、求函数y=kx+b和y= 的表达式;(2)、已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.22. 在等腰△ABC中,AB=BC , 点D , E在射线BA上,BD=DE , 过点E作EF∥BC , 交射线CA于点F . 请解答下列问题: (1)、当点E在线段AB上,CD是△ACB的角平分线时,如图①,求证:AE+BC=CF;(提示:延长CD , FE交于点M . )(2)、当点E在线段BA的延长线上,CD是△ACB的角平分线时,如图②;当点E在线段BA的延长线上,CD是△ACB的外角平分线时,如图③,请直接写出线段AE , BC , CF之间的数量关系,不需要证明;23. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.
(1)、当点E在线段AB上,CD是△ACB的角平分线时,如图①,求证:AE+BC=CF;(提示:延长CD , FE交于点M . )(2)、当点E在线段BA的延长线上,CD是△ACB的角平分线时,如图②;当点E在线段BA的延长线上,CD是△ACB的外角平分线时,如图③,请直接写出线段AE , BC , CF之间的数量关系,不需要证明;23. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,交AC边于点E,点F是弧EB的中点,∠C=90°,连接AF.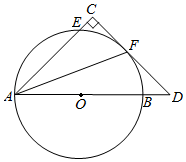 (1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.24. 综合与实践
(1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.24. 综合与实践问题情境:
如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE′(点A的对应点为点C).延长AE交CE′于点F , 连接DE .
猜想证明:
 (1)、试判断四边形BE'FE的形状,并说明理由;(2)、如图②,若DA=DE , 请猜想线段CF与FE'的数量关系并加以证明;
(1)、试判断四边形BE'FE的形状,并说明理由;(2)、如图②,若DA=DE , 请猜想线段CF与FE'的数量关系并加以证明;解决问题:
(3)、如图①,若AB=15,CF=3,请求出DE的长.25. 如图,抛物线经过点 、 、 . (1)、求抛物线的解析式;(2)、点 是抛物线上的动点,当 时,试确定m的值,使得 的面积最大;(3)、抛物线上是否存在不同于点B的点D,满足 ,若存在,请求出点D的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点 是抛物线上的动点,当 时,试确定m的值,使得 的面积最大;(3)、抛物线上是否存在不同于点B的点D,满足 ,若存在,请求出点D的坐标;若不存在,请说明理由.