山东省潍坊安丘市、高密市2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. 9的算术平方根是( )A、3 B、±3 C、 D、±2. 下列数学符号中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的( )A、 B、 C、 D、4. 截止到2021年4月6日,电影《你好,李焕英》累计票房达到53.96亿元,进入全球前100名,同时贾玲成为了全球票房最高的女导演,其中数据53.96亿用科学记数法表示为( )A、53.96×108 B、5.396×1010 C、0.5396×1010 D、5.396×1095. 若关于x的一元二次方程(a−1)x2−2x+2=0有实数根,则整数a的最大值为( )
3. 下列计算正确的( )A、 B、 C、 D、4. 截止到2021年4月6日,电影《你好,李焕英》累计票房达到53.96亿元,进入全球前100名,同时贾玲成为了全球票房最高的女导演,其中数据53.96亿用科学记数法表示为( )A、53.96×108 B、5.396×1010 C、0.5396×1010 D、5.396×1095. 若关于x的一元二次方程(a−1)x2−2x+2=0有实数根,则整数a的最大值为( )
A、﹣1 B、0 C、1 D、26. 如图,是某中学九(3)班学生外出方式(乘车、步行、骑车)的不完整频数(人数)分布直方图.如果乘车的频率是0.4,那么步行的频率为( )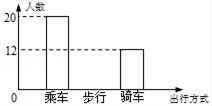 A、0.4 B、0.36 C、0.3 D、0.247. 如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).
A、0.4 B、0.36 C、0.3 D、0.247. 如图,在半径为2的⊙O中,将劣弧AB沿弦AB翻折,折叠后的弧AB恰好与OA、OB相切,则阴影部分的面积为( ).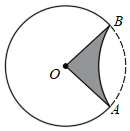 A、4﹣π B、4+π C、π﹣2 D、π+28. 如图,等腰△ABC中,AB=AC=5cm , BC=8cm . 动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E , 连接ED . 当直线DE与⊙O相切时,t的取值是( )
A、4﹣π B、4+π C、π﹣2 D、π+28. 如图,等腰△ABC中,AB=AC=5cm , BC=8cm . 动点D从点C出发,沿线段CB以2cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随时停止.设运动时间为t(s),以点O为圆心,OB长为半径的⊙O与BA交于另一点E , 连接ED . 当直线DE与⊙O相切时,t的取值是( )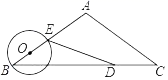 A、 B、 C、 D、9. 如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC , 点F在CD的延长线上,AF∥BC , 则下列结论错误的是( )
A、 B、 C、 D、9. 如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC , 点F在CD的延长线上,AF∥BC , 则下列结论错误的是( )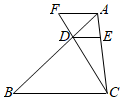 A、 B、 C、 D、10. 函数 与 (a≠0)在同一直角坐标系中的图象可能是( )A、
A、 B、 C、 D、10. 函数 与 (a≠0)在同一直角坐标系中的图象可能是( )A、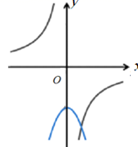 B、
B、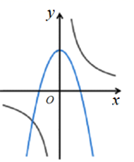 C、
C、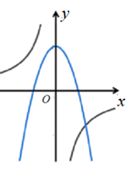 D、
D、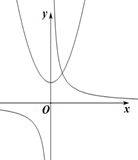 11. 如图,四边形ABCD为菱形,BF∥AC , DF交AC的延长线于点E , 交BF于点F , 且CE:AC=1:2.则下列结论错误的有( )
11. 如图,四边形ABCD为菱形,BF∥AC , DF交AC的延长线于点E , 交BF于点F , 且CE:AC=1:2.则下列结论错误的有( )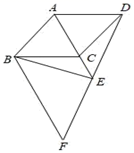 A、△ABE≌△ADE; B、∠CBE=∠CDF; C、DE=FE; D、S△BCE:S四边形ABFD=1:9
A、△ABE≌△ADE; B、∠CBE=∠CDF; C、DE=FE; D、S△BCE:S四边形ABFD=1:9二、填空题
-
12. 定义运算a⊗b=a2-2ab+1,下面给出了关于这种运算的几个结论其中正确的
A. 2⊗5=-15;
B. 不等式组 的解集为x<- ;
C. 方程2x⊗1=0是一元一次方程;
D. 方程 ⊗x= +x的解是x=-1.13. 已知x+y=3,xy=-2,则代数式x2y+xy2的值为 .14. 已知a , b , c , d的平均数是4,则2a+1,2b+1,2c+1,2d+1的平均数是 .15. 如图,半径为 的⊙ 与边长为 的等边三角形 的两边 、 都相切,连接 ,则 .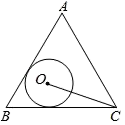 16. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而减小,且-4≤x≤1时,y的最大值为7,则a的值为17. 如图,矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',A'B'与AD相交于点G , 若点F , B',D在同一条直线上,△A'EG的面积为4,△CDF的面积为36,则△GB'D的面积等于 .
16. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而减小,且-4≤x≤1时,y的最大值为7,则a的值为17. 如图,矩形ABCD沿EF折叠,点A的对称点为点A',点B的对称点为点B',A'B'与AD相交于点G , 若点F , B',D在同一条直线上,△A'EG的面积为4,△CDF的面积为36,则△GB'D的面积等于 .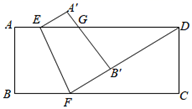 18. 如果记y= =f(x),并且f(1)表示当x=1时y的值.即f(1)= = ;f( )表示当x= 时y的值,f( )= = …,那么f(-1)+f(-2)+f(- )+f(-3)+f(- )+…+f(-2021)+f(- )= .
18. 如果记y= =f(x),并且f(1)表示当x=1时y的值.即f(1)= = ;f( )表示当x= 时y的值,f( )= = …,那么f(-1)+f(-2)+f(- )+f(-3)+f(- )+…+f(-2021)+f(- )= .三、解答题
-
19.(1)、计算:(2)、解不等式组: ,并把它的解集在数轴上表示出来.
 20. 某市为了加快5G网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点A测得发射塔顶端P点的仰角是45°,向前走90米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.(结果精确到1米, )
20. 某市为了加快5G网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点A测得发射塔顶端P点的仰角是45°,向前走90米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.(结果精确到1米, )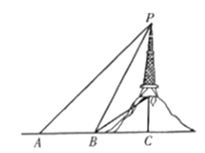 21. 如图,已知AB是O的直径,CD⊥AB , 垂足为点E , 如果BE=OE , AB=10cm,求△ACD的周长 .
21. 如图,已知AB是O的直径,CD⊥AB , 垂足为点E , 如果BE=OE , AB=10cm,求△ACD的周长 .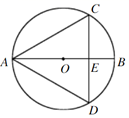 22. 某校举行了“防溺水”知识竞赛.八年级两个班各选派10名同学参加预赛,依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示).
22. 某校举行了“防溺水”知识竞赛.八年级两个班各选派10名同学参加预赛,依据各参赛选手的成绩(均为整数)绘制了统计表和折线统计图(如图所示).班级
八(1)班
八(2)班
最高分
100
99
众数
98
中位数
96
平均数
94.8
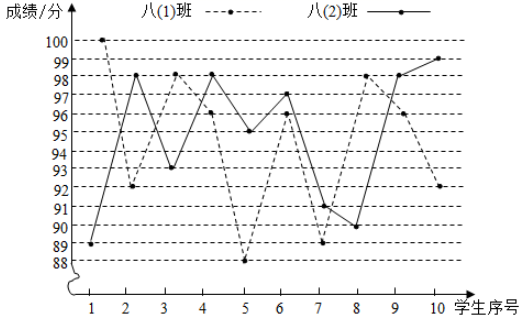 (1)、统计表中,a= , b= , c=;(2)、若从两个班的预赛选手中选四名学生参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在成绩为98分的学生中任选两个,求另外两个决赛名额落在不同班级的概率.23. 阅读与思考
(1)、统计表中,a= , b= , c=;(2)、若从两个班的预赛选手中选四名学生参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在成绩为98分的学生中任选两个,求另外两个决赛名额落在不同班级的概率.23. 阅读与思考下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
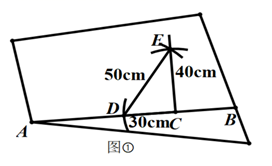
今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过 上的一点 ,作出 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?
办法一:如图①,可利用一把有刻度的直尺在 上量出 ,然后分别以 , 为圆心,以 与 为半径画圆弧,两弧相交于点 ,作直线 ,则 必为 .

办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 , 两点,然后把木棒斜放在木板上,使点 与点 重合,用铅笔在木板上将点 对应的位置标记为点 ,保持点 不动,将木棒绕点 旋转,使点 落在 上,在木板上将点 对应的位置标记为点 .然后将 延长,在延长线上截取线段 ,得到点 ,作直线 ,则 .
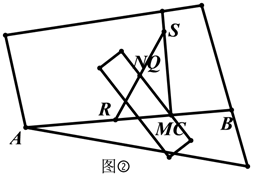
我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢?
……
任务:
(1)、填空;“办法一”依据的一个数学定理是;(2)、根据“办法二”的操作过程,证明 ;(3)、①尺规作图:请在图③的木板上,过点 作出 的垂线(在木板上保留作图痕迹,不写作法);②说明你的作法依据的数学定理或基本事实(写出一个即可)
24. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x(元/件)
4
5
6
y(件)
10000
9500
9000
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于15元/件时,每销售一件商品便向某慈善机构捐赠m元( ),捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请直接写出m的取值范围.25. 如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D , 与y轴的交点为C . 过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA , OB , DA和DB .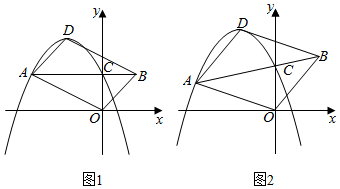 (1)、如图1,当AC∥x轴时,
(1)、如图1,当AC∥x轴时,①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c .
(2)、如图2,若b=﹣2, = ,是否存在这样的点A , 使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.