山东省青岛市李沧区2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. 下列电视台的台标,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列选项中,对 的说法错误的是( ).A、 的相反数是 B、 的倒数是 C、 的绝对值是 D、 是有理数3. 某中学在芦山地震捐款活动中,共捐款二十一万三千元.这一数据用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元4. 如图是一个几何体的三视图,则这个几何体是( ).
2. 下列选项中,对 的说法错误的是( ).A、 的相反数是 B、 的倒数是 C、 的绝对值是 D、 是有理数3. 某中学在芦山地震捐款活动中,共捐款二十一万三千元.这一数据用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元4. 如图是一个几何体的三视图,则这个几何体是( ). A、三棱锥 B、圆锥 C、三棱柱 D、圆柱5. 一次数学测试后,某小组五名同学的成绩及数据分析如下表所示(有两个数据被遮盖),那么被遮盖的两个数据依次是( ).
A、三棱锥 B、圆锥 C、三棱柱 D、圆柱5. 一次数学测试后,某小组五名同学的成绩及数据分析如下表所示(有两个数据被遮盖),那么被遮盖的两个数据依次是( ).甲
乙
丙
丁
戊
方差
平均成绩
81
79
■
80
82
■
80
A、78, B、78,2 C、80, D、80,26. 下列运算正确的是( ).A、 B、 C、 D、7. 如图,△ABC内接于⊙O,∠A=50°.E是边BC的中点,连接OE并延长,交⊙O于点D,连接BD,则∠D的大小为( )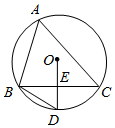 A、55° B、65° C、60° D、75°8. 二次函数 的顶点坐标为(-1,n),其部分图象如图所示.以下结论错误的是( ).
A、55° B、65° C、60° D、75°8. 二次函数 的顶点坐标为(-1,n),其部分图象如图所示.以下结论错误的是( ). A、 B、 C、 D、关于 的方程 无实数根
A、 B、 C、 D、关于 的方程 无实数根二、填空题
-
9. 计算: .10. 为改善生态环境,防止水土流失,某村计划在荒坡上种1000棵树.由于青年志愿者的支援,每天比原计划多种25%,结果提前5天完成任务,则该村原计划每天种树棵.11. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是

12. 如图,正方形 的边长为2,点 在 轴的正半轴上,点 在 轴的负半轴上,将正方形 绕点 逆时针旋转30°至正方形 的位置, 与 相交于点 ,则点 的坐标为 .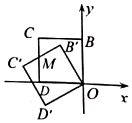 13. 如图,以等边三角形 的 边为直径画半圆,分别交 , 于点 , , 是圆的切线,过点 作 的垂线交 于点 .若 的长为2,则 的长为 .
13. 如图,以等边三角形 的 边为直径画半圆,分别交 , 于点 , , 是圆的切线,过点 作 的垂线交 于点 .若 的长为2,则 的长为 . 14. 如图,在 中, , , ,点 是射线 上一动点,连接 ,将 沿 折叠,当点 的对应点 落在线段 的垂直平分线上时, 的长等于.
14. 如图,在 中, , , ,点 是射线 上一动点,连接 ,将 沿 折叠,当点 的对应点 落在线段 的垂直平分线上时, 的长等于.
三、解答题
-
15. 已知:如图,四边形 .
求作:点 ,使点 在四边形 内部, ,并且点 到 两边的距离相等.
 16.(1)、化简: ;(2)、解不等式组: .17. 某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:
16.(1)、化简: ;(2)、解不等式组: .17. 某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表:某校150名学生上学方式频数分布表
方式
划记
频数
步行
正正正
15
骑车
正正正正正正正正正正一
51
乘公共交通工具
正正正正正正正正正
45
乘私家车
正正正正正正
30
其它
正

9
合计
150

 (1)、理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)、根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)、该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地.请你结合上述统计的全过程,再提出一条合理化建议.18. 某中学举行“中国梦•我的梦”演讲比赛.九年级(1)班的小明和小刚都想参加.现设计了如下游戏规则:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去,这个游戏规则是否公平?并说明理由.19. 图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
(1)、理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;(2)、根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;(3)、该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地.请你结合上述统计的全过程,再提出一条合理化建议.18. 某中学举行“中国梦•我的梦”演讲比赛.九年级(1)班的小明和小刚都想参加.现设计了如下游戏规则:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去,这个游戏规则是否公平?并说明理由.19. 图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:课题
测量“马踏飞燕”雕塑最高点离地面的高度
测量示意图

如图,雕塑的最高点B到地面的高度为 ,在测点C用仪器测得点B的仰角为 ,前进一段距离到达测点E,再用该仪器测得点B的仰角为 ,且点A,B,C,D,E,F均在同一竖直平面内,点A,C,E在同一条直线上.
测量数据
的度数
的度数
的长度
仪器 ( )的高度
5米
米
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据: , , , , , )
 20. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .
20. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .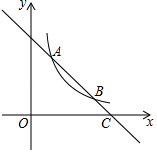 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.21. 如图,在 与 中, , , , 相交于点 .过点 作 交 的延长线于点 ,过点 作 交 的延长线于点 , , 相交于点 .
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.21. 如图,在 与 中, , , , 相交于点 .过点 作 交 的延长线于点 ,过点 作 交 的延长线于点 , , 相交于点 . (1)、求证: ≌ ;(2)、若 ,四边形 是什么特殊四边形?请说明理由.22. 某商店销售一种商品,经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如表:
(1)、求证: ≌ ;(2)、若 ,四边形 是什么特殊四边形?请说明理由.22. 某商店销售一种商品,经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如表:售价 (元/件)
50
60
80
周销售量 (件)
100
80
40
周销售利润 (元)
1000
1600
1600
注:周销售利润=周销售量×(售价-进价)
(1)、求当售价是多少元/件时,周销售利润最大;(2)、由于某种原因,该商品进价提高了 元/件 ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求 的值.23. (问题)用n边形的对角线把n边形分割成(n-2个三角形,共有多少种不同的分割方案 ?(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有 种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以, .


探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?不妨把分割方案分成三类:



第1类:如图③,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
第2类:如图④,用点 , 与 连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为 种分割方案.
第3类:如图⑤,用点 , 与 连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有f(4)种不同的分割方案,所以,此类共有f(4)种不同的分割方案.
所以, (种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?不妨把分割方案分成四类:
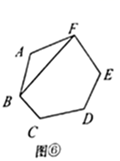
第1类:如图⑥,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案,所以,此类共有 种不同的分割方案.
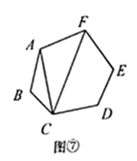
第2类:如图⑦,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
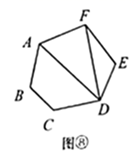
第3类:如图⑧,用 , 与 连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有 种不同的分割方案.所以,此类共有 种分割方案.
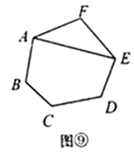
第4类:如图,用 , 与 连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有 种不同的分割方案.所以,此类共有 种分割方案.
所以,
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则 与 的关系为 ,共有种不同的分割方案.
……
(结论)用 边形的对角线把 边形分割成 个三角形,共有多少种不同的分割方案 ?(直接写出 与 之间的关系式,不写解答过程)
(应用)用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论中的关系式求解)
24. 如图,矩形 中, , , 是 边上的一点, , 是 边的中点,动点 从点 出发,沿边 以 的速度向终点 运动,过点 作 于点 ,连接 ,设动点 的运动时间是 .

 (1)、求 为何值时, ?(2)、设 的面积为 ,写出 与 之间的函数关系式;(3)、当 平分四边形 的面积时,求 的值;(4)、是否存在时刻 ,使得点 关于 的对称点 ,落在线段 上,若存在,求出 值,若不存在,说明理由.
(1)、求 为何值时, ?(2)、设 的面积为 ,写出 与 之间的函数关系式;(3)、当 平分四边形 的面积时,求 的值;(4)、是否存在时刻 ,使得点 关于 的对称点 ,落在线段 上,若存在,求出 值,若不存在,说明理由.