山东省济南市历下区2021年中考数学三模试卷

试卷更新日期：2021-06-29 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 如图所示的物体，其左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 世界上最小的动物是原生动物中的一种同肋膜肺炎菌相似的单细胞动物，它只有0.1微米长，即0.0000001米，只有在显微镜下才能看得到．其中数字0.0000001用科学记数法表示为（）

A、0.1×10^﹣5 B、1×10^﹣7 C、﹣1×10⁵ D、10×10^﹣4

查看试题解析
4. 如图，已知a//b，一块含30°角的直角三角板，如图所示放置，∠2＝30°，则∠1等于（　）

A、110° B、130° C、150° D、160°

查看试题解析
5. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $AlphaGo$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
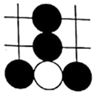6. 若分式 $\frac{x^{2} - 4}{x - 2}$ 有意义，则x满足的条件是（　　）

A、x＝2 B、x≠2 C、x≠±2 D、x＞2

查看试题解析
7. 实数a ， b在数轴上对应点的位置如图所示，下列判断正确的是（）

A、 $| a | < 1$ B、 $a b > 0$ C、 $a + b > 0$ D、 $1 - a > 1$

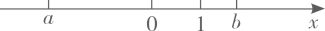查看试题解析
8. 下列说法正确的是（　　）

A、调查大明湖的水质情况，采用普查的方式 B、在连续5次数学测试中，两名同学的平均分相同，方差较大的同学成绩更稳定 C、一组数据3、6、6、7、9的众数是6 D、从2000名学生中随机抽取100名学生进行调查，样本容量为2000名学生

查看试题解析
9. 已知一次函数 $y = (k - 2) x - m$ 的图象与 $y$ 轴的负半轴相交，且函数值 $y$ 随自变量 $x$ 增大而减小，则下列结论正确的是（）

A、 $k < 2$ ， $m > 0$ B、 $k < 2$ ， $m < 0$ C、 $k > 2$ ， $m > 0$ D、 $k < 0$ ， $m < 0$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，按以下步骤作图：①以点 $A$ 为圆心，以小于 $A C$ 的长为半径作弧，分别交 $A C$ ， $A B$ 于点 $M$ ， $N$ ；②分别以点 $M$ ， $N$ 为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点 $P$ ；③连接 $A P$ ，交 $B C$ 于点 $D$ ．若 $C D = 3$ ， $B D = 5$ ，则 $A C$ 的长为（）

A、4 B、5 C、6 D、7

查看试题解析
11. 3月26日，济南轨道交通2号线开始初期运营，如路线图中所示，已知腊山南站到北园站直线距离AD长约21千米，从腊山南站到二环西路站的长AB约为4千米，路线的转弯角 $∠ B$ 为157.5°， $∠ C$ 为150°，又测得 $∠ D$ ＝30°，则从二环西路站到济泺路站的距离BC的长为（）（tan22.5°≈0.6，sin22.5°≈0.4，cos22.5°≈0.9， $\sqrt{3}$ ≈1.7）

A、14.62千米 B、14.64千米 C、14.66千米 D、14.68千米

查看试题解析
12. 如图1，在Rt△ABC中，∠A＝90°，BC＝10cm，点P ，点Q同时从点B出发，点P以2cm/s的速度沿B→A→C运动，终点为C ，点Q出发t秒时，△BPQ的面积为ycm² ，已知y与t的函数关系的图象如图2（曲线OM和MN均为抛物线的一部分），给出以下结论：①AC＝6cm；②曲线MN的解析式为y＝﹣ $\frac{4}{5}$ t²＋ $\frac{28}{5}$ t（4≤t≤7）；③线段PQ的长度的最大值为 $\frac{6}{5} \sqrt{10}$ cm；④若△PQC与△ABC相似，则t＝ $\frac{40}{7}$ 秒，其中正确的说法是（　　）

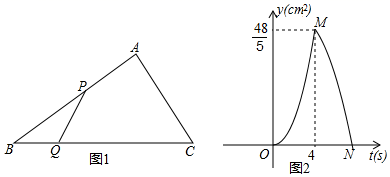A、①②④ B、②③④ C、①③④ D、①②③

查看试题解析

二、填空题

13. 分解因式：m²n＋4mn＝．

查看试题解析
14. 如图，一个可以自由转动的转盘，任意转动转盘一次，当转盘停止时，指针落在红色区域的概率为．

查看试题解析
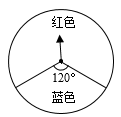15. 若x=1是一元二次方程x²+2x+m=0的一个根，则m的值为．

查看试题解析
16. 如图，矩形ABCD中，AB=1，AD= $\sqrt{2}$ ．以A为圆心，AD的长为半径做弧交BC边于点E ，则图中 $\overset{⌢}{D E}$ 的弧长是.

查看试题解析
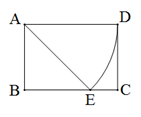17. 如图，一个等腰直角三角尺不小心掉到两墙之间，已知∠ACB＝90°，AC＝BC ，从三角尺的刻度可知AB＝20cm，AD为三块砖的厚度，BE为两块砖的厚度，小聪很快就知道了砌墙所用砖块的厚度为cm．

查看试题解析
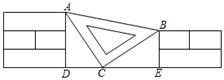18. 规定：如果一个四边形有一组对边平行，一组邻边相等，那么称此四边形为广义菱形．根据规定判断下面四个结论：①正方形和菱形都是广义菱形；②对角线互相垂直，且两组邻边分别相等的四边形是广义菱形；③一组对边平行，一条对角线平分一个内角的四边形是广义菱形；④若M、N的坐标分别为（0，2），（0， $-$ 2），P是二次函数 $y = \frac{1}{8} x^{2}$ 图象上在第一象限内的任意一点，PQ垂直直线 $y = - 2$ 于点Q ，则四边形PMNQ是广义菱形．其中正确的是．（填序号）

查看试题解析

三、解答题

19. 计算： ${(\sqrt{2021} - \sqrt{2022})}^{0} + {(- \frac{1}{2})}^{- 1} - | 2 \cos 60 ° - 1 |$ ．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 (x + 1) > 0 \\ \frac{x - 7}{2} < - 1 \end{array}$ ，并写出所有整数解．

查看试题解析
21. 如图，在平行四边形ABCD中，AE ， CF分别平分∠BAD和∠DCB ，且AE ， CF分别交BD于点E ， F ．求证：BE＝DF ．

查看试题解析

22. 为了调查学生对防溺水知识的了解情况，甲、乙两校进行了相关知识测试，在两校各随机抽取20名学生的测试成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．

a ．甲校20名学生成绩的频数分布表和频数分布直方图如图：

甲校学生样本成绩频数分布表

成绩m（分）	频数（人）	频率
50≤m＜60	a	0.05
60≤m＜70	b	c
70≤m＜80	3	0.15
80≤m＜90	8	0.40
90≤m＜100	6	0.30
合计	20	1.00

b ．甲校成绩在80≤m＜90的这一组的具体成绩是：86；86；87；87；88；89；89；89

c ．甲、乙两校成绩的统计数据如表所示：

学校	平均分	中位数	众数
甲	83.7	m	89
乙	84.2	85	85

根据以如图表提供的信息，解答下列问题：

(1)、表中a＝；m＝；

(2)、补全甲校学生样本成绩频数分布直方图；

(3)、在此次测试中，某学生的成绩是86分，在他所属学校排在前10名，由表中数据可知该学生是校的学生（填“甲”或“乙”）；

(4)、若甲校共有1200人，成绩不低于80分为“优秀”，则甲校成绩“优秀”的人数约为多少人？

查看试题解析

23. 如图，AB是⊙O直径，点C在⊙O上，AD平分∠CAB ， BD是⊙O的切线，AD与BC相交于点E ，与⊙O相交于点F ，连接BF ．

(1)、求证：BD＝BE；

(2)、若DE＝4，BD＝2 $\sqrt{5}$ ，求AE的长．

查看试题解析
24. 一项工程，甲，乙两公司合做，12天可以完成，共需付施工费102000元；如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．

(1)、甲，乙两公司单独完成此项工程，各需多少天？

(2)、若让一个公司单独完成这项工程，哪个公司的施工费较少？

查看试题解析
25. Rt△ABC在直角坐标系内的位置如图所示，反比例函数y＝ $\frac{k}{x}$ （k≠0）在第一象限内的图象与BC边交于点D（4，1），与AB边交于点E（2，n）．

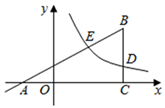(1)、求反比例函数的解析式和n值；

(2)、当 $\frac{B C}{A C}$ ＝ $\frac{1}{2}$ 时，求直线AB的解析式；

(3)、设P是线段AB边上的点，在（2）的条件下，是否存在点P ，以B、C、P为顶点的三角形与△EDB相似？若存在，请直接写出此时点P的坐标；若不存在，请说明理由．

查看试题解析
26. 在Rt△ABC中，AC＝BC＝5，∠C＝90°，D是AC边上一点， $\frac{C D}{A D} = \frac{2}{3}$ ，直线DE交BC于点E ．

(1)、如图1，若DE∥AB ， CD＝， EB＝；

(2)、如图2，在（1）的条件下，等腰Rt△CMN的端点M在直线DE上运动，连接EN ，请判断DM与NE的关系，并说明理由；

(3)、如图3，若∠CDE＝60°，等腰Rt△CMN的端点M点在直线DE上运动，连接NB ，请直接写出NB的最小值．

查看试题解析
27. 已知抛物线y＝ax²＋2ax＋c与x轴交于A（－3，0），B两点，交y轴于点C（0，－3）．

(1)、求抛物线的解析式；

(2)、如图1，点P在抛物线的对称轴上，P的纵坐标为n ，若－3＜n＜0，以C、P为顶点作正方形CPDE（C、P、D、E顺时针排列），若正方形CPDE有两个顶点在抛物线上，求n的值；

(3)、如图2，C、F两点关于对称轴对称，直线y＝kx＋b（k＜0）过点F ，且与抛物线有且只有一个交点，平移直线y＝kx＋b交抛物线于G ， H两点（点G在点H上方），请判断∠GCF与∠HCF的数量关系，并说明理由．

查看试题解析