辽宁省沈阳市沈河区2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. -2021的相反数是( )A、2021 B、-2021 C、 D、2. 下列几何体的主视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )A、 B、 C、 D、4. 若 下列选项中,正确的是( )A、 B、 C、 D、5. 若正多边形的一个内角是 ,则这个正多边形的边数为( )A、12 B、10 C、8 D、76. 分式方程 的解是( )A、 B、 C、 D、7. 若实数 , 满足 ,则 的值为( )A、1 B、2 C、3 D、48. 如图,按以下步骤进行尺规作图:(1)以点 为圆心,任意长为半径作弧,交 的两边 , 分别于 , 两点;(2)分别以点 , 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;(3)作射线 ,连接 , , .下列结论错误的是( )
3. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )A、 B、 C、 D、4. 若 下列选项中,正确的是( )A、 B、 C、 D、5. 若正多边形的一个内角是 ,则这个正多边形的边数为( )A、12 B、10 C、8 D、76. 分式方程 的解是( )A、 B、 C、 D、7. 若实数 , 满足 ,则 的值为( )A、1 B、2 C、3 D、48. 如图,按以下步骤进行尺规作图:(1)以点 为圆心,任意长为半径作弧,交 的两边 , 分别于 , 两点;(2)分别以点 , 为圆心,大于 的长为半径作弧,两弧在 内交于点 ;(3)作射线 ,连接 , , .下列结论错误的是( ) A、 垂直平分 B、 C、 D、9. 如图,在正方形方格纸中,每个小正方形的边长都是1,点 , , , 都在格点处, 与 相交于点 ,则 的值是( )
A、 垂直平分 B、 C、 D、9. 如图,在正方形方格纸中,每个小正方形的边长都是1,点 , , , 都在格点处, 与 相交于点 ,则 的值是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系 中, 的顶点 坐标为 , . 轴,且 ,将 沿着 轴的方向向下平移 个单位, , 两点的对应点同时落在函数 的图象上,则k的值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系 中, 的顶点 坐标为 , . 轴,且 ,将 沿着 轴的方向向下平移 个单位, , 两点的对应点同时落在函数 的图象上,则k的值为( ) A、45 B、42 C、 D、
A、45 B、42 C、 D、二、填空题
-
11. 分解因式: = .12. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数 (单位:千克)及方差 ,如下表所示.今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是 . (填“甲”或“乙”或“丙”或“丁”)
甲
乙
丙
丁
24
24
23
20
2.1
1.9
2
1.9
13. 如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为 ,若在坡度为 的山坡上种树,也要求株距为10m,那么相邻两棵树间的坡面距离为m. 14. 如图,点 , , 在 上, , , , 的长为 .
14. 如图,点 , , 在 上, , , , 的长为 . 15. 某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为元.16. 如图,在 中, , , ,点 在射线 上,过点 作 .且 ,使点 , , 按逆时针方向排列,连接 ,当 是等腰三角形时,线段 的长度是 .
15. 某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为元.16. 如图,在 中, , , ,点 在射线 上,过点 作 .且 ,使点 , , 按逆时针方向排列,连接 ,当 是等腰三角形时,线段 的长度是 .
三、解答题
-
17. 计算:18. 某校有4个测温通道,分别记为 、 、 、 ,学生可随机选取其中的一个通道测温进校园.选择任意一个测温通道的可能性是相同的.(1)、某日早晨小王同学进校园选择 测温通道的概率是;(2)、某日早晨小王和小李两位同学选择不同的测温通道进校园,请用画树状图或列表法求小王选择 通道,小李选择 通道测温进校园的概率.19. 如图,在 中,过点 作 于点 ,点 在边 上, .连接 , .
 (1)、求证:四边形 是矩形;(2)、若 , 平分 , ,则四边形 的周长是 .20. 我市某学校为落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图:
(1)、求证:四边形 是矩形;(2)、若 , 平分 , ,则四边形 的周长是 .20. 我市某学校为落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人必选且只选一类最喜欢的课程),将调查结果绘制成如图所示的两幅不完整的统计图: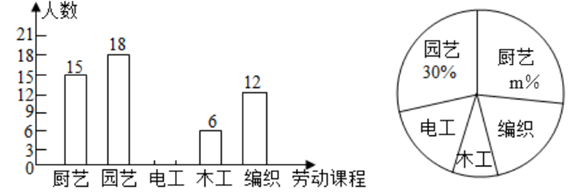
请根据统计图提供的信息,解答下列问题:
(1)、本次随机调查的学生人数为人;(2)、请在答题卡上直接补全条形统计图;(3)、扇形统计图中 的值为 , 木工所在的扇形圆心角大小是;(4)、若该校七年级共有1000名学生,请估计该校七年级学生选择“编织”劳动课程的人数.21. 某商场出售的电脑原价为每台5000元,元旦期间开展了促销活动,将原价经过两次下调后,促销价为每台4050元.(1)、求平均每次下调的百分率;(2)、临近春节,该店决定推出力度更大的促销活动,按(1)中的百分率第三次下调销售价,若该电脑的进货价为每台3000元,则此次促销中每台电脑的利润为元.22. 如图,在 中, ,以 为直径的 交 于点 , 垂直于过点 的切线,垂足为点 . (1)、求证: 平分 ;(2)、若 , ,则 的半径长为 .23. 如图,在直角坐标系 中,直线 : 与 轴、 轴分别交于点 , ,线段 上一动点 从点 以每秒2个单位长度的速度向点 运动,同时线段 上一动点 从点 以每秒 个单位长度的速度向点 运动,当其中一点到达终点时另一点随之停止运动,设运动时间为 秒( ), 的面积为 .
(1)、求证: 平分 ;(2)、若 , ,则 的半径长为 .23. 如图,在直角坐标系 中,直线 : 与 轴、 轴分别交于点 , ,线段 上一动点 从点 以每秒2个单位长度的速度向点 运动,同时线段 上一动点 从点 以每秒 个单位长度的速度向点 运动,当其中一点到达终点时另一点随之停止运动,设运动时间为 秒( ), 的面积为 . (1)、点 的坐标是 , 点 的坐标是;(2)、求 关于 的函数解析式;(3)、在运动过程中,当 的值第一次等于5时,将 沿 轴的正方向平移.得到 ,点 , , 分别对应点 , 交 于点 ,若点 分线段 成 ,请直接写出点 的坐标.24. 在 中, , , ,动点 在边 上,连接 .
(1)、点 的坐标是 , 点 的坐标是;(2)、求 关于 的函数解析式;(3)、在运动过程中,当 的值第一次等于5时,将 沿 轴的正方向平移.得到 ,点 , , 分别对应点 , 交 于点 ,若点 分线段 成 ,请直接写出点 的坐标.24. 在 中, , , ,动点 在边 上,连接 .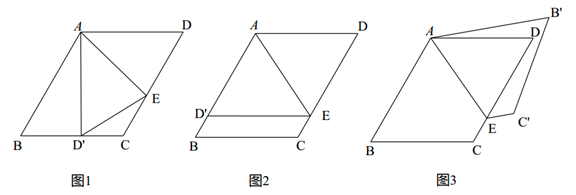 (1)、如图1,将 沿着 所在直线折叠,得到 ,点 的对应点是 .
(1)、如图1,将 沿着 所在直线折叠,得到 ,点 的对应点是 .①如图2,当点 落在 边上时线段 的长度是 , 并判断四边形 的形状,请说明理由;
②当 时,线段 的长度是;
(2)、如图,将四边形 沿着 所在直线折叠,得到四边形 ,其中点 , 的对应点是 , ,当 经过点 时,请直接写出线段 的长度.25. 如图,在直角坐标系 中,抛物线 与 轴交于点 和 ,与 轴交于点 ,点 是抛物线上的动点(不与点 、 、 重合). (1)、求抛物线的解析式;(2)、当点 在第一象限时,设 的面积为 , 的面积为 ,当 时,求点 的坐标;(3)、过点 作直线 ,点 是直线 上的动点,当 ,且 时,请直接写出点 的坐标.
(1)、求抛物线的解析式;(2)、当点 在第一象限时,设 的面积为 , 的面积为 ,当 时,求点 的坐标;(3)、过点 作直线 ,点 是直线 上的动点,当 ,且 时,请直接写出点 的坐标.