广东省广州市南沙区2021年中考数学一模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
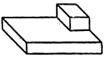
1. 如图中,与图中几何体对应的三视图是( )
 A、
A、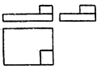 B、
B、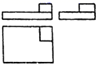 C、
C、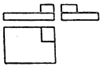 D、
D、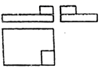 2. 近年来,我国5G发展取得明显成效,截至2020年底,全国建设开通5基站达71.8万个,将数据71.8万用科学记数法表示为( )A、0.718×106 B、7.18×105 C、71.8×104 D、718×1033. 下列算式中,计算正确的是( )A、 =﹣3 B、|3﹣π|=3﹣π C、(﹣3ab)2=6a2b2 D、3﹣3=4. 已知2a+1和5是正数b的两个平方根,则a+b的值是( )A、25 B、30 C、20 D、225. 已知点A(﹣2,3)经变换后到点B , 下面的说法正确的是( )A、点A先向上平移3个单位,再向左平移4个单位到点B , 则点B的坐标为B(2,6) B、点A绕原点按顺时针方向旋转90°后到点B , 则点B的坐标为B(3,2) C、点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2) D、点A与点B关于x轴对称,则点B的坐标为B(2,3)6. 如图,四边形ABCD内接于⊙O , E为DC延长线上一点.若∠BCE=105°,则∠BOD的度数是( )
2. 近年来,我国5G发展取得明显成效,截至2020年底,全国建设开通5基站达71.8万个,将数据71.8万用科学记数法表示为( )A、0.718×106 B、7.18×105 C、71.8×104 D、718×1033. 下列算式中,计算正确的是( )A、 =﹣3 B、|3﹣π|=3﹣π C、(﹣3ab)2=6a2b2 D、3﹣3=4. 已知2a+1和5是正数b的两个平方根,则a+b的值是( )A、25 B、30 C、20 D、225. 已知点A(﹣2,3)经变换后到点B , 下面的说法正确的是( )A、点A先向上平移3个单位,再向左平移4个单位到点B , 则点B的坐标为B(2,6) B、点A绕原点按顺时针方向旋转90°后到点B , 则点B的坐标为B(3,2) C、点A与点B关于原点中心对称,则点B的坐标为B(3,﹣2) D、点A与点B关于x轴对称,则点B的坐标为B(2,3)6. 如图,四边形ABCD内接于⊙O , E为DC延长线上一点.若∠BCE=105°,则∠BOD的度数是( ) A、150° B、105° C、75° D、165°7. 为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如表:
A、150° B、105° C、75° D、165°7. 为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如表:月用水量/吨
3
4
6
10
12
户数/户
2
4
3
2
1
则关于这若干户家庭的用水量,下列说法错误的是( )
A、众数是4 B、平均数是7 C、调查了12户家庭的月用水量 D、中位数是58. 参加足球联赛的每两支球队之间都要进行两场比赛,共要比赛240场,设参加比赛的球队有x支,根据题意,下面列出的方程正确的是( )A、x(x﹣1)=240 B、 x(x﹣1)=240 C、x(x+1)=240 D、 x(x+1)=2409. 对于实数m , n , 先定义一种新运算“⊗”如下:m⊗n= ,若x⊗(﹣2)=10,则实数x等于( )A、3 B、﹣4 C、8 D、3或810. 如图,抛物线y=ax2﹣2ax﹣3a(a≠0)与x轴交于点A , B . 与y轴交于点C . 连接AC、BC . 已知△ABC的面积为3.将抛物线向左平移h(h>0)个单位,记平移后抛物线中y随着x的增大而增大的部分为H . 当直线BC与H没有公共点时,h的取值范围是( )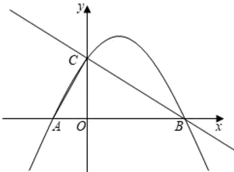 A、h> B、0<h≤ C、h>2 D、0<h<2
A、h> B、0<h≤ C、h>2 D、0<h<2二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围 .12. 分解因式:ab2﹣9a= .13. 如图,∠ACD是△ABC的外角,CE∥AB , ∠ACB=75°,∠ECD=45°,则∠A的度数为 .
 14. 如图,在直角坐标系中,点A(0,6)、B(0,﹣2)、C(﹣4,6),则△ABC外接圆的圆心坐标为 .
14. 如图,在直角坐标系中,点A(0,6)、B(0,﹣2)、C(﹣4,6),则△ABC外接圆的圆心坐标为 . 15. 已知关于x的一元二次方程m2x2+(2m+1)x+1=0有实数根,则m的取值范围是 .16. 如图,在矩形ABCD中,AB=4,AD=5,E是CD边上一点,连结AE , 将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G , 连结DG . 点M、N分别是线段AG , DG上的动点(与端点不重合),且∠DMN=∠DAM , 以下结论:①CE=2;②DM2=DN•AF;③DN最小值为1;④若△DMN为等腰三角形,则点M的位置有三种不同情况.其中正确的是 .
15. 已知关于x的一元二次方程m2x2+(2m+1)x+1=0有实数根,则m的取值范围是 .16. 如图,在矩形ABCD中,AB=4,AD=5,E是CD边上一点,连结AE , 将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G , 连结DG . 点M、N分别是线段AG , DG上的动点(与端点不重合),且∠DMN=∠DAM , 以下结论:①CE=2;②DM2=DN•AF;③DN最小值为1;④若△DMN为等腰三角形,则点M的位置有三种不同情况.其中正确的是 .
三、解答题
-
17. 解二元一次方程组18. 如图,∠B=∠E , ∠1=∠2,BC=EC .
求证:AB=DE .
 19. A=(2x+y)2﹣(2x+y)(2x﹣y)﹣2y2 .(1)、化简A;(2)、若点(x , y)在第四象限,请选择合适的整数代入,求此时A的值.20. 如图,身高为1.6米的小明在距离一棵大树10米的点B处看大树顶端C的仰角为45°,在大树的另一边点A处看这棵大树顶端C的仰角度数为 .(A、E、B在同一条直线上,忽略眼睛到头顶间距离.)
19. A=(2x+y)2﹣(2x+y)(2x﹣y)﹣2y2 .(1)、化简A;(2)、若点(x , y)在第四象限,请选择合适的整数代入,求此时A的值.20. 如图,身高为1.6米的小明在距离一棵大树10米的点B处看大树顶端C的仰角为45°,在大树的另一边点A处看这棵大树顶端C的仰角度数为 .(A、E、B在同一条直线上,忽略眼睛到头顶间距离.) (1)、求大树的高度.(2)、若点A与点B之间的距离为(10+10 )米,求 的值.21. 2020年,新冠肺炎疫情突如其来,各大中小幼学校延期开学,实行“停课不停教不停学”,网络直播教学成为其中最常见的教学方式,某区为了解九年级老师使用线上授课软件情况,在4月份某天随机抽查了若干名老师进行调查,其中A表示“一起中学”,B表示“腾讯会议”,C表示“腾讯课堂”,D表示“QQ群课堂”,E表示“钉钉”,现将调查结果绘制成两种不完整的统计图表:
(1)、求大树的高度.(2)、若点A与点B之间的距离为(10+10 )米,求 的值.21. 2020年,新冠肺炎疫情突如其来,各大中小幼学校延期开学,实行“停课不停教不停学”,网络直播教学成为其中最常见的教学方式,某区为了解九年级老师使用线上授课软件情况,在4月份某天随机抽查了若干名老师进行调查,其中A表示“一起中学”,B表示“腾讯会议”,C表示“腾讯课堂”,D表示“QQ群课堂”,E表示“钉钉”,现将调查结果绘制成两种不完整的统计图表:组别
使用人数(人)
占调查人数的百分率
A
3
5%
B
12
20%
C
a
35%
D
15
c
E
b
15%
请根据图表中的信息解答下列问题:
 (1)、b= , 并将频数分布直方图补充完整;(2)、已知该区共有九年级老师500人,请你估计该区使用“QQ群课堂”有多少人?(3)、该区计划在A组随机抽取两人了解使用情况,已知A组有理科老师2人,文科老师1人,请用列举法求出抽取两名老师都是理科老师的概率.22. 某学校计划购买甲、乙两种品牌的洗手液,乙品牌洗手液每瓶的价格比甲品牌洗手液每瓶价格的2倍少12元,已知用320元购买甲品牌洗手液的数量与用400元购买乙品牌洗手液的数量相同.(1)、求甲、乙两种品牌洗手液每瓶的价格各是多少元?(2)、若该学校从超市一次性购买甲、乙两种品牌的洗手液共100瓶,且总费用不超过1645元,则最多可以购买多少瓶乙品牌洗手液?23. 如图,菱形ABCD的边BC在x轴上,点A在y轴上,对角线AC、BD交于点E , 且BC=5,菱形ABCD的面积为24.
(1)、b= , 并将频数分布直方图补充完整;(2)、已知该区共有九年级老师500人,请你估计该区使用“QQ群课堂”有多少人?(3)、该区计划在A组随机抽取两人了解使用情况,已知A组有理科老师2人,文科老师1人,请用列举法求出抽取两名老师都是理科老师的概率.22. 某学校计划购买甲、乙两种品牌的洗手液,乙品牌洗手液每瓶的价格比甲品牌洗手液每瓶价格的2倍少12元,已知用320元购买甲品牌洗手液的数量与用400元购买乙品牌洗手液的数量相同.(1)、求甲、乙两种品牌洗手液每瓶的价格各是多少元?(2)、若该学校从超市一次性购买甲、乙两种品牌的洗手液共100瓶,且总费用不超过1645元,则最多可以购买多少瓶乙品牌洗手液?23. 如图,菱形ABCD的边BC在x轴上,点A在y轴上,对角线AC、BD交于点E , 且BC=5,菱形ABCD的面积为24.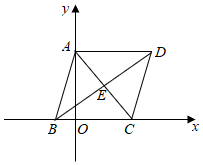 (1)、求点A的坐标;(2)、求AC+BD的值;(3)、若反比例函数y= 经过点E , 且与边AD交于点F , 过点F作FG垂直x轴于点G , 请求出△BFG的面积.24. 如图,⊙O的直径AB为10cm,弦AC为6cm.
(1)、求点A的坐标;(2)、求AC+BD的值;(3)、若反比例函数y= 经过点E , 且与边AD交于点F , 过点F作FG垂直x轴于点G , 请求出△BFG的面积.24. 如图,⊙O的直径AB为10cm,弦AC为6cm. (1)、作∠ACB的角平分线交⊙O于点D , 连接AD、BD(尺规作图.并保留作图痕迹);(2)、求线段CD的长度;(3)、若点G在劣弧BD上由点B运动到点D时,求弦CG的中点K运动的路径长.25. 已知,抛物线y=mx2+ x﹣4m与x轴交于点A(﹣4,0)和点B , 与y轴交于点C . 点D(n , 0)为x轴上一动点,且有﹣4<n<0,过点D作直线1⊥x轴,且与直线AC交于点M , 与抛物线交于点N , 过点N作NP⊥AC于点P . 点E在第三象限内,且有OE=OD .
(1)、作∠ACB的角平分线交⊙O于点D , 连接AD、BD(尺规作图.并保留作图痕迹);(2)、求线段CD的长度;(3)、若点G在劣弧BD上由点B运动到点D时,求弦CG的中点K运动的路径长.25. 已知,抛物线y=mx2+ x﹣4m与x轴交于点A(﹣4,0)和点B , 与y轴交于点C . 点D(n , 0)为x轴上一动点,且有﹣4<n<0,过点D作直线1⊥x轴,且与直线AC交于点M , 与抛物线交于点N , 过点N作NP⊥AC于点P . 点E在第三象限内,且有OE=OD . (1)、求m的值和直线AC的解析式.(2)、若点D在运动过程中, AD+CD取得最小值时,求此时n的值.(3)、若点△ADM的周长与△MNP的周长的比为5∶6时,求AE+ CE的最小值.
(1)、求m的值和直线AC的解析式.(2)、若点D在运动过程中, AD+CD取得最小值时,求此时n的值.(3)、若点△ADM的周长与△MNP的周长的比为5∶6时,求AE+ CE的最小值.