安徽省志诚教育教育集团十校联盟2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2021 B、 C、1 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 目前,第五代移动通信技术(5G)正在阔步前行,按照产业间的关联关系测算,2020年,5G间接拉动GDP增长将超过4190亿元,数据“4190亿”用科学记数法表示为( )A、4.19×103 B、0.4190×104 C、4.19×1011 D、419×1094. 如图,下列关于物体的主视图画法正确的是( )
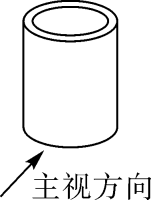 A、
A、 B、
B、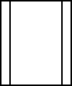 C、
C、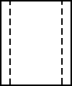 D、
D、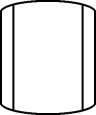 5. 一元二次方程(x-1)(x+5)=3x+1的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根6. 一个质地均匀的正四面体,四个面上分别写着数字 将它投掷于桌面上,连续投掷两次,则两次与桌面接触的面上的数字之和为5的概率是( )A、 B、 C、 D、7. 如图.在 中, ,D是边AB的中点,E是边BC上一点.若DE平分 的周长,则DE的长为( )
5. 一元二次方程(x-1)(x+5)=3x+1的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、只有一个实数根6. 一个质地均匀的正四面体,四个面上分别写着数字 将它投掷于桌面上,连续投掷两次,则两次与桌面接触的面上的数字之和为5的概率是( )A、 B、 C、 D、7. 如图.在 中, ,D是边AB的中点,E是边BC上一点.若DE平分 的周长,则DE的长为( )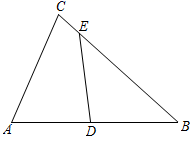 A、 B、 C、 D、18. 2018年底,安徽省高铁里程约1400公里,2019年底,安徽省高铁里程约1900公里,若高铁里程的年增长率保持不变,则估计2021年底安徽高铁里程约 ( )A、2584公里 B、3000公里 C、3500公里 D、3800公里9. 四边形 中, ,点P,Q是对角线BD上不同的两点,若四边形 是菱形,则下列说法中错误的是 ( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( )
A、 B、 C、 D、18. 2018年底,安徽省高铁里程约1400公里,2019年底,安徽省高铁里程约1900公里,若高铁里程的年增长率保持不变,则估计2021年底安徽高铁里程约 ( )A、2584公里 B、3000公里 C、3500公里 D、3800公里9. 四边形 中, ,点P,Q是对角线BD上不同的两点,若四边形 是菱形,则下列说法中错误的是 ( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=5,AB=3 ,点E在AB上, = ,在矩形内找一点P,使得∠BPE=60°,则线段PD的最小值为( ) A、4 B、2 C、2 -2 D、2 -4
A、4 B、2 C、2 -2 D、2 -4二、填空题
-
11. 因式分解: .12. 直角三角形斜边上的中线等于斜边的一半逆命题13. 如图,已知 的半径为2, 内接于 , ,则 .
 14. 如图(1),四边形 是正方形,点E是边AD上的点,将 沿着直线CE折叠,使得点D落在AC上,对应点为点F.
14. 如图(1),四边形 是正方形,点E是边AD上的点,将 沿着直线CE折叠,使得点D落在AC上,对应点为点F. (1)、 ;(2)、如图(2),点G是BC上的点,将 沿着直线AG折叠,使得点B落在AC上,对应点为H,连接 ,则 .
(1)、 ;(2)、如图(2),点G是BC上的点,将 沿着直线AG折叠,使得点B落在AC上,对应点为H,连接 ,则 .三、解答题
-
15. 计算:16. 中国古代入民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题,原文:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?17. 观察下面由“※”组成的图案和算式,并解答问题:
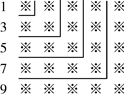
,
,
,
.
(1)、试猜想 ;(2)、试猜想 ;(3)、按上述规律计算: 的值.18. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点)及过格点的直线l. (1)、画出△ABC关于直线l对称的△A1B1C1;(2)、将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;(3)、以A、A1、A2为顶点的三角形中,tan∠A2AA1= .19. 中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图所示.其工作原理主要利用光的反射原理,已知 共线, 于点B,入射角 , (入射角等于反射角), 米,求OB的高度.(参考数据: )
(1)、画出△ABC关于直线l对称的△A1B1C1;(2)、将△ABC向上平移3个单位长度,再向左平移1个单位长度,画出平移后的△A2B2C2;(3)、以A、A1、A2为顶点的三角形中,tan∠A2AA1= .19. 中国古代人在公元前2世纪就制成了世界上最早的潜望镜,西汉初年成书的《淮南万毕术》中有这样的记载:“取大镜高悬,悬水盆于其下,则见四邻矣.”如图所示.其工作原理主要利用光的反射原理,已知 共线, 于点B,入射角 , (入射角等于反射角), 米,求OB的高度.(参考数据: ) 20. 如图,在 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D.
20. 如图,在 中,以O为圆心,OA为半径的圆与BC相切与点B,与OC相交于点D. (1)、求 的度数.(2)、如图,点E在⊙O上,连接CE与⊙O交于点F,若 ,求 的度数.21. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.
(1)、求 的度数.(2)、如图,点E在⊙O上,连接CE与⊙O交于点F,若 ,求 的度数.21. 我市某中学举行“法制进校园”知识竞赛,赛后将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图.请你根据统计图解答下列问题.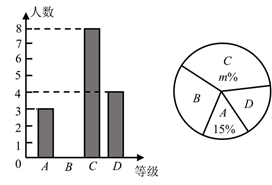 (1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.
(1)、成绩为“B等级”的学生人数有名;(2)、在扇形统计图中,表示“D等级”的扇形的圆心角度数为 , 图中m的值为;(3)、学校决定从本次比赛获得“A等级”的学生中选出2名去参加市中学生知识竞赛.已知“A等级”中有1名女生,请用列表或画树状图的方法求出女生被选中的概率.