安徽省宿州市埇桥区2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
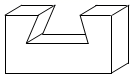
1. 100的相反数是( ).A、100 B、 C、 D、2. 下列运算正确的是( ).A、 B、 C、 D、3. 如图所示,左边立体图形的俯视图为( ).
 A、
A、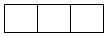 B、
B、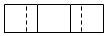 C、
C、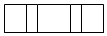 D、
D、 4. 2021年第一季度安徽省GDP达 亿元,进入全国前十,其中 亿用科学记数法表示为( ).A、 B、 C、 D、5. 已知关于 的方程 有两个相等的实数根,则 的值为( ).A、 B、0 C、1 D、46. 随着我国新能源汽车的生产技术不断提升,市场上某款新能源汽车的价格由今年3月份的270000元/辆下降到5月份的243000元/辆.若价格继续下降,且月平均降价的百分率保持不变,则预测到今年7月份该款新能源汽车的价格将会( ).(参考数据: )A、低于22万元/辆 B、低于 万元/辆 C、超过22万元/辆 D、超过23万元/辆7. 某企业2020年6~10月生产利润的变化情况如折线图所示,下列说法与图中反映的信息相符的是( ).
4. 2021年第一季度安徽省GDP达 亿元,进入全国前十,其中 亿用科学记数法表示为( ).A、 B、 C、 D、5. 已知关于 的方程 有两个相等的实数根,则 的值为( ).A、 B、0 C、1 D、46. 随着我国新能源汽车的生产技术不断提升,市场上某款新能源汽车的价格由今年3月份的270000元/辆下降到5月份的243000元/辆.若价格继续下降,且月平均降价的百分率保持不变,则预测到今年7月份该款新能源汽车的价格将会( ).(参考数据: )A、低于22万元/辆 B、低于 万元/辆 C、超过22万元/辆 D、超过23万元/辆7. 某企业2020年6~10月生产利润的变化情况如折线图所示,下列说法与图中反映的信息相符的是( ). A、6~7月份利润的增长快于7~8月份利润的增长 B、6~10月份利润的方差为14000(万元)2 C、6~10月份利润的众数是1300万元 D、6~10月份利润的中位数为1300万元8. 已知,凸四边形 ,给出下列四个条件:
A、6~7月份利润的增长快于7~8月份利润的增长 B、6~10月份利润的方差为14000(万元)2 C、6~10月份利润的众数是1300万元 D、6~10月份利润的中位数为1300万元8. 已知,凸四边形 ,给出下列四个条件:① , ② ,
③ , ④ ,
能判断四边形 是平行四边形的个数是( ).
A、1 B、2 C、3 D、49. 在平面直角坐标系中,直线 与 轴、 轴分别交于 、 ,已知抛物线 经过点 ,且顶点 在直线 的上方,则 的取值范围是( ).A、 B、 且 C、 且 D、10. 如图,在矩形 中, , ,点 在 上,点 在 上,且 ,连接 , ,则 的最小值为( ). A、10 B、11 C、12 D、13
A、10 B、11 C、12 D、13二、填空题
-
11. = .12. 因式分解: .13. 如图,在 中, , ,以点 为圆心的弧与 相切于点 ,分别交 、 于点 、 ,若 ,则图中阴影部分的面积为 . (结果保留 )
 14. 如图,线段 ,射线 于点 ,射线 于点 ,点 为 的中点, 为射线 上一动点,将 沿 翻折得到 , 、 的延长线分别交射线 、 于点 、 ,连接 .请探究下列问题:
14. 如图,线段 ,射线 于点 ,射线 于点 ,点 为 的中点, 为射线 上一动点,将 沿 翻折得到 , 、 的延长线分别交射线 、 于点 、 ,连接 .请探究下列问题: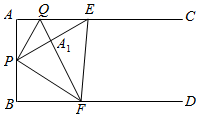 (1)、 的值为;(2)、当 ∽ 时, .
(1)、 的值为;(2)、当 ∽ 时, .三、解答题
-
15. 解方程: .16. 在如图所示的网格中建立平面直角坐标系, 的顶点在网格线的交点上,点 的坐标为 .
 (1)、画出 向上平移4个单位长度得到的 ,并写出点 的对应点 的坐标;(2)、画出 绕原点 顺时针旋转90°得到的 ,并写出点 的对应点 的坐标.17. 观察下列等式:
(1)、画出 向上平移4个单位长度得到的 ,并写出点 的对应点 的坐标;(2)、画出 绕原点 顺时针旋转90°得到的 ,并写出点 的对应点 的坐标.17. 观察下列等式:第1个等式: ;
第2个等式: ;
第3个等式: ;
…
按照以上规律,解决下列问题:
(1)、写出第4个等式:;(2)、写出你猜想的第 个等式:(用含 的等式表示),并证明.18. 如图,在数学综合实践活动中,某小组想要测量某条河的宽度 ,小组成员在专业人员的协助下利用无人机进行测量,在 处测得 , 两点的俯角分别为45°和30°(即 , ).若无人机离地面的高度 为120米,且点 , , 在同一水平直线上,求这条河的宽度 .(结果精确到1米).(参考数据: , )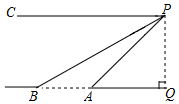 19. 如图,已知 过圆 的圆心 ,且弦 ,连接 交 于点 ,连接 交 于点 ,连接 、 .
19. 如图,已知 过圆 的圆心 ,且弦 ,连接 交 于点 ,连接 交 于点 ,连接 、 .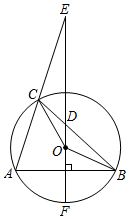 (1)、若 ,求 的度数;(2)、若 , ,求 的长,20. 如图,正比例函数 与反比例函数 的图象交于点 ,且点 的纵坐标为8.过点 作 轴于点 .
(1)、若 ,求 的度数;(2)、若 , ,求 的长,20. 如图,正比例函数 与反比例函数 的图象交于点 ,且点 的纵坐标为8.过点 作 轴于点 . (1)、求 的值:(2)、点 在线段 上,若 ,
(1)、求 的值:(2)、点 在线段 上,若 ,①求 的长:
②点 为 轴负半轴上动点,当 与 的面积相等时,请直接写出所有正确的点 的坐标.
21. 某中学为了解本校九年级女生“一分钟仰卧起坐”项目的成绩情况,从九年级随机抽取部分女生进行该项目测试,并将测试的成绩( 次)数据,绘制成频数分布表和扇形统计图.部分信息如下,根据提供的信息解答下列问题:组号
分组
频数
①
3
②
15
③
④
10
⑤
2
 (1)、m= , 在扇形统计图中第③小组对应的扇形的圆心角度数为°;(2)、若测试九年级女生“一分钟仰卧起坐”次数不低于44次的成绩为优秀,本校九年级女生共有360人,请估算该校九年级女生“一分钟仰卧起坐”成绩为优秀的人数;(3)、把在第①小组内的三个女生分别记为: 、 、 ,把在第⑤小组内的两个女生分别记为: 、 ,从第①小组和第⑤小组总共5个女生中随机抽取2个女生进行“你对中考体育考试选项的看法”的问卷调查,求第①小组和第⑤小组都有1个女生被选中的概率.22. 某校了解学生午餐排队情况,发现学生排队累计的人数 (人)随时间 (分钟)的变化情况满足关系式 ,其中 . 与 的部分对应值如下表:
(1)、m= , 在扇形统计图中第③小组对应的扇形的圆心角度数为°;(2)、若测试九年级女生“一分钟仰卧起坐”次数不低于44次的成绩为优秀,本校九年级女生共有360人,请估算该校九年级女生“一分钟仰卧起坐”成绩为优秀的人数;(3)、把在第①小组内的三个女生分别记为: 、 、 ,把在第⑤小组内的两个女生分别记为: 、 ,从第①小组和第⑤小组总共5个女生中随机抽取2个女生进行“你对中考体育考试选项的看法”的问卷调查,求第①小组和第⑤小组都有1个女生被选中的概率.22. 某校了解学生午餐排队情况,发现学生排队累计的人数 (人)随时间 (分钟)的变化情况满足关系式 ,其中 . 与 的部分对应值如下表:时间 (分钟)
0
1
2
…
累计人数 (人)
0
58
112
…
(1)、求 与 之间的函数解析式;(2)、若食堂就餐排队窗口每分钟可减少排队人数32人,求排队等待的学生人数最多时有多少人?(排队等待的学生人数=排队累计的人数减少的排队人数)(3)、排队等待5分钟后,为减少排队等候时间,食堂临时增加就餐排队窗口,现每分钟可减少排队人数48人,再过分钟后刚好不再出现排队等待的情况.23. 如图1,在 中, , ,点 是 上一点,连接 ,过点 作 ,交 的延长线于点 ,过点 作 于点 . (1)、求证: ≌ ;(2)、如图2,点 是 的中点,连接 , .
(1)、求证: ≌ ;(2)、如图2,点 是 的中点,连接 , .①求 的度数:
②当 ,且点 为 中点时,求 的面积.