安徽省c20教育联盟2021年中考数学二模试卷
试卷更新日期:2021-06-29 类型:中考模拟
一、单选题
-
1. 2021年1月8日,安徽多地气温创20年来最低,其中最低气温合肥-11℃、安庆-8.5℃、蚌埠-11.5℃、池州-8.9℃,在以上四个城市中最低气温中最高的是( )A、合肥 B、蚌埠 C、安庆 D、池州2. 下列运算正确的是( )A、 B、 C、 D、3. 国家统计局1月18日公布,初步核算,2020我国国内生产总值(GDP),约为1016000亿元,其中1016000亿用科学记数法表示为( )A、 B、 C、 D、4. 如图,一副直角三角板的顶点 重合( , ),当 时,则∠ABD=( )
 A、105° B、75° C、85° D、95°5. 初中生骑电动车上学存在安全隐患,为了解某初中2200个学生家长对“中学生骑电动车上学”的态度,从中随机调查200个家长,结果有160个家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有160个家长持反对态度 C、样本是200个家长 D、该校约有80%的家长持反对态度6. 如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( )
A、105° B、75° C、85° D、95°5. 初中生骑电动车上学存在安全隐患,为了解某初中2200个学生家长对“中学生骑电动车上学”的态度,从中随机调查200个家长,结果有160个家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有160个家长持反对态度 C、样本是200个家长 D、该校约有80%的家长持反对态度6. 如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( ) A、270° B、216° C、108° D、135°7. 若 , 是方程组 的解, , , 都在反比例函数 上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,点 , , , 都在⊙O上,且 ,AB=AD , S四边形ABCD =( )
A、270° B、216° C、108° D、135°7. 若 , 是方程组 的解, , , 都在反比例函数 上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,点 , , , 都在⊙O上,且 ,AB=AD , S四边形ABCD =( ) A、 B、 C、 D、69. 如图,直角坐标系中,点G的坐标为(2,0),点F是y轴上任意动点,FG绕点F逆时针旋转90°得FH , 则动点H总在下列哪条直线上( )
A、 B、 C、 D、69. 如图,直角坐标系中,点G的坐标为(2,0),点F是y轴上任意动点,FG绕点F逆时针旋转90°得FH , 则动点H总在下列哪条直线上( ) A、 B、 C、 D、10. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )
A、 B、 C、 D、10. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )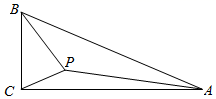 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
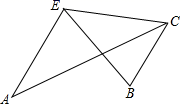
11. 不等式 的最大正整数解是 .12. 若 ,且 .则 .13. 如图, , ,∠BEC=40°,则 °.
 14. 如图,Rt△BAC , ∠ACB=30°,∠BAC=90°,将Rt△BAC绕点A旋转一定度数,点C与点C'重合,点B与点B'重合,当C、B、C'三点在同一条直线时,请完成下列探究:
14. 如图,Rt△BAC , ∠ACB=30°,∠BAC=90°,将Rt△BAC绕点A旋转一定度数,点C与点C'重合,点B与点B'重合,当C、B、C'三点在同一条直线时,请完成下列探究: (1)、这个旋转角=°;(2)、此时, .
(1)、这个旋转角=°;(2)、此时, .三、解答题
-
15. 先化简,再求值: ,其中 ,并从 的范围中选一个你喜欢的又有意义的一个整数值代入求值.16. 今年开学,由于疫情防控的需要,某学校统一购置口罩(1)班全体学生配备了一定数量的口罩,若每个学生发3个口罩,则多30个口罩,若给每个学生发5个口罩,则少50个口罩,请问该班有多少名学生?17. 如图,点 的坐标为 ,点 的坐标为
①以点 为旋转中心,将 顺时针方向旋转90°,得到 ;
②以点 为位似中心,将 放大 ,使相似比为 ,且点 在第三象限.
(1)、在图中画出 和 ;(2)、请直接写出点 的坐标:( , )(3)、在上面的(2)问下,直接写出在线段 上的任意动点 的对应点 的坐标:( , ). 18. 如图,是一组完全相同的黑白小球组成的图形
18. 如图,是一组完全相同的黑白小球组成的图形
观察上面各图及对应的关系式,根据发现的规律,解决下列问题:
(1)、写出第6个等式:;(2)、写出你猜想的第n个等式:(用含 的等式表示,并证明其符合题意性)19. 如图, 且 于点 ,DC⊥BC于点C , , . (1)、求 , 的值;(2)、连接 ,求 的长.20. 如图∠AOC=90°,且OA=OC , 点D在以OA为直径的半圆上,圆心为点P , 连接CD并延长交OA的延长线于点B , 且AB=4,∠BDA=∠BOD .
(1)、求 , 的值;(2)、连接 ,求 的长.20. 如图∠AOC=90°,且OA=OC , 点D在以OA为直径的半圆上,圆心为点P , 连接CD并延长交OA的延长线于点B , 且AB=4,∠BDA=∠BOD . (1)、求证: 为⊙P的切线;(2)、求该半圆的面积.21. 本周末校园专场招聘会,某大学金融学院200名学生参加某国有银行的甲、乙、丙三个部门的定向招聘(每个人都参加了报名,每人都只能报一个部门),他们到各个部门报名人数百分比所对应的圆心角如图(部门录取人数÷部门报名人数)×100%
(1)、求证: 为⊙P的切线;(2)、求该半圆的面积.21. 本周末校园专场招聘会,某大学金融学院200名学生参加某国有银行的甲、乙、丙三个部门的定向招聘(每个人都参加了报名,每人都只能报一个部门),他们到各个部门报名人数百分比所对应的圆心角如图(部门录取人数÷部门报名人数)×100%部门
甲
乙
丙
录取率
30%
40%
60%
(1)、到乙部门报名人数有人,甲部门的录取人数为人,该企业的总体录取率为%.(2)、如果到甲部门报名的人员中有一些人员改到丙部门报名,在保持各部门录取率不变的情况下,该企业的总体录取率恰好增加6%,问有多少人从甲部门改到丙部门报名?(3)、3位好同学:小明,小强,小刚分别报名甲、乙、丙三个部门,均被录取,辅导员将三封该企业录取通知(信封外表完全一样)混在一起交给他们三人,他们同时打开,请问他们三人同时打开恰好都属于自己的录取通知的概率是多少? 22. 某超市3月份购进一批牛肉销售,比去年同期进价降16元/千克,去年3月份购买80千克的牛肉的钱,今年3月份可以购买100千克的牛肉.(1)、今年3月份购进这批牛肉每千克多少元?(2)、若今年3月份该超市购进牛肉后每天的牛肉销售量 (千克)与销售单价 (元/千克)满足如图所示的一次函数关系.求 与 之间的函数关系式;(3)、这批牛肉的销售单价定为x元/千克,每天的所有其他成本共计为200元/天,且66≤x≤80,求今年3月份该超市销售牛肉每天利润的取值范围?(利润=销售收入-进货金额-其他成本)
22. 某超市3月份购进一批牛肉销售,比去年同期进价降16元/千克,去年3月份购买80千克的牛肉的钱,今年3月份可以购买100千克的牛肉.(1)、今年3月份购进这批牛肉每千克多少元?(2)、若今年3月份该超市购进牛肉后每天的牛肉销售量 (千克)与销售单价 (元/千克)满足如图所示的一次函数关系.求 与 之间的函数关系式;(3)、这批牛肉的销售单价定为x元/千克,每天的所有其他成本共计为200元/天,且66≤x≤80,求今年3月份该超市销售牛肉每天利润的取值范围?(利润=销售收入-进货金额-其他成本) 23. 如图1各点坐标 , , .
23. 如图1各点坐标 , , .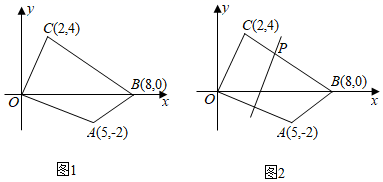 (1)、求证: ;(2)、发现与操作:小明通过操作后,发现 恰好将四边形 面积平分,请问为什么?小刚说:除了线段 外,我还可以再找到一条线段将该四边形面积也平分?(画出一条即可,并解释这样做的原因)(3)、如图2,小强作 的垂直平分线交 于点 ,请你求出点 的坐标及过程?
(1)、求证: ;(2)、发现与操作:小明通过操作后,发现 恰好将四边形 面积平分,请问为什么?小刚说:除了线段 外,我还可以再找到一条线段将该四边形面积也平分?(画出一条即可,并解释这样做的原因)(3)、如图2,小强作 的垂直平分线交 于点 ,请你求出点 的坐标及过程?