上海市2021年中考数学试卷

试卷更新日期：2021-06-28 类型：中考真卷

进入出卷网下载

一、单选题

1. 下列实数中，有理数是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{\frac{1}{4}}$ D、 $\sqrt{\frac{1}{5}}$

查看试题解析
2. 下列单项式中， $a^{2} b^{3}$ 的同类项是（）

A、 $a^{3} b^{2}$ B、 $2 a^{2} b^{3}$ C、 $a^{2} b$ D、 $a b^{3}$

查看试题解析
3. 将抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 向下平移两个单位，以下说法错误的是（）

A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变

查看试题解析
4. 商店准备一种包装袋来包装大米，经市场调查以后，做出如下统计图，请问选择什么样的包装最合适（）

A、 $2 kg$ /包 B、 $3 kg$ /包 C、 $4 kg$ /包 D、 $5 kg$ /包

查看试题解析
5. 如图，已知平行四边形ABCD中， $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ ，E为 $A B$ 中点，求 $\frac{1}{2} \vec{a} + \vec{b} =$ （）

A、 $\vec{E C}$ B、 $\vec{C E}$ C、 $\vec{E D}$ D、 $\vec{D E}$

查看试题解析
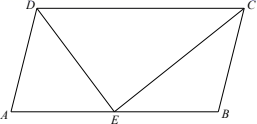6. 如图，已知长方形 $A B C D$ 中， $A B = 4 ， A D = 3$ ，圆B的半径为1，圆A与圆B内切，则点 $C ， D$ 与圆A的位置关系是（）

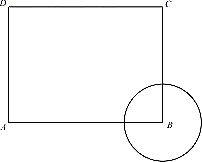A、点C在圆A外，点D在圆A内 B、点C在圆A外，点D在圆A外 C、点C在圆A上，点D在圆A内 D、点C在圆A内，点D在圆A外

查看试题解析

二、填空题

7. 计算： $x^{7} \div x^{2} =$ ．

查看试题解析
8. 已知 $f (x) = \frac{6}{x}$ ，那么 $f (\sqrt{3}) =$ ．

查看试题解析
9. 已知 $\sqrt{x + 4} = 3$ ，则 $x =$ ．

查看试题解析
10. 不等式 $2 x - 12 < 0$ 的解集是．

查看试题解析
11. $70 °$ 的余角是．

查看试题解析
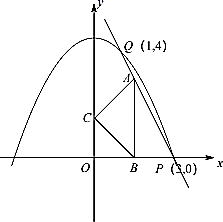
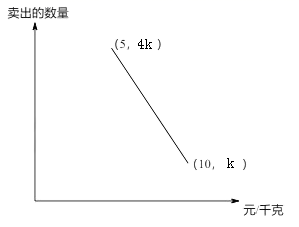
12. 若一元二次方程 $2 x^{2} - 3 x + c = 0$ 无解，则c的取值范围为．

查看试题解析
13. 有数据 $1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21 ， 34$ ，从这些数据中取一个数据，得到偶数的概率为．

查看试题解析
14. 已知函数 $y = k x$ 经过二、四象限，且函数不经过 $(- 1 ， 1)$ ，请写出一个符合条件的函数解析式．

查看试题解析
15. 某人购进一批苹果到集贸市场零售，已知卖出的苹果数量与售价之间的关系如图所示，成本为5元/千克，现以8元/千克卖出，赚元．

查看试题解析
16. 如图，已知 $\frac{S_{△ A B D}}{S_{△ B C D}} = \frac{1}{2}$ ，则 $\frac{S_{△ B O C}}{S_{△ B C D}} =$ ．

查看试题解析
17. 六个带 $30 °$ 角的直角三角板拼成一个正六边形，直角三角板的最短边为1，求中间正六边形的面积．

查看试题解析
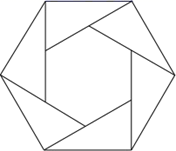18. 定义：在平面内，一个点到图形的距离是这个点到这个图上所有点的最短距离，在平面内有一个正方形，边长为2，中心为O，在正方形外有一点 $P ， O P = 2$ ，当正方形绕着点O旋转时，则点P到正方形的最短距离d的取值范围为．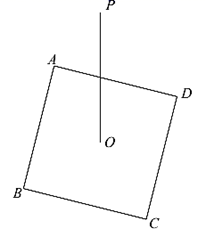

查看试题解析

三、解答题

19. 计算： $9^{\frac{1}{2}} + | 1 - \sqrt{2} | - 2^{- 1} \times \sqrt{8}$

查看试题解析
20. 解方程组： ${\begin{array}{l} x + y = 3 \\ x^{2} - 4 y^{2} = 0 \end{array}$

查看试题解析
21. 已知在 $△ A B D$ 中， $A C ⊥ B D ， B C = 8 ， C D = 4$ ， $\cos ∠ A B C = \frac{4}{5}$ ， $B F$ 为 $A D$ 边上的中线．

(1)、求 $A C$ 的长；

(2)、求 $\tan ∠ F B D$ 的值．

查看试题解析
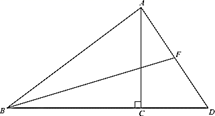22. 现在5G手机非常流行，某公司第一季度总共生产80万部5G手机，三个月生产情况如下图．

(1)、求三月份共生产了多少部手机?

(2)、 $5 G$ 手机速度很快，比 $4 G$ 下载速度每秒多 $95 MB$ ，下载一部 $1000 MB$ 的电影， $5 G$ 比 $4 G$ 要快190秒，求 $5 G$ 手机的下载速度．

查看试题解析
23. 已知：在圆O内，弦 $A D$ 与弦 $B C$ 交于点 $G ， A D = C B ， M ， N$ 分别是 $C B$ 和 $A D$ 的中点，联结 $M N ， O G$ ．

(1)、求证： $O G ⊥ M N$ ；

(2)、联结 $A C ， A M ， C N$ ，当 $C N / / O G$ 时，求证：四边形 $A C N M$ 为矩形．

查看试题解析
24. 已知抛物线 $y = a x^{2} + c (a \neq 0)$ 过点 $P (3 ， 0) ， Q (1 ， 4)$ ．

(1)、求抛物线的解析式；

(2)、点A在直线 $P Q$ 上且在第一象限内，过A作 $A B ⊥ x$ 轴于B，以 $A B$ 为斜边在其左侧作等腰直角 $A B C$ ．
①若A与Q重合，求C到抛物线对称轴的距离；

②若C落在抛物线上，求C的坐标．

查看试题解析
25. 如图，在梯形 $A B C D$ 中， $A D / / B C ， ∠ A B C = 90 ° ， A D = C D ， O$ 是对角线 $A C$ 的中点，联结 $B O$ 并延长交边 $C D$ 或边 $A D$ 于E．

(1)、当点E在边 $C D$ 上时，
①求证： $△ D A C ∽ △ O B C$ ；

②若 $B E ⊥ C D$ ，求 $\frac{A D}{B C}$ 的值；

(2)、若 $D E = 2 ， O E = 3$ ，求 $C D$ 的长．

查看试题解析