江苏省淮安市六校联盟2020-2021学年高一上学期数学第三次学情调查试卷
试卷更新日期:2021-06-28 类型:月考试卷
一、单选题
-
1. 已知集合M={1,2,3,4},N={-2,2},下列结论成立的是( )A、N M B、M∪N=M C、M∩N=N D、M∩N={2}2. 设命题 ,则 为( )A、 B、 C、 D、3. 的定义域为( )A、 B、 C、 D、4. 已知 , , ,则 , , 的大小关系为( )A、 B、 C、 D、5. 已知α是第二象限角, 为其终边上一点,且cosα=x,则x等于( )A、 B、 C、 D、6. 已知曲线 且 过定点 ,若 且 ,则 的最小值为( ).A、 B、9 C、5 D、7. 函数 的图象大致为( )A、
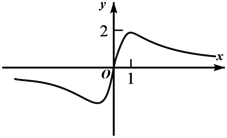 B、
B、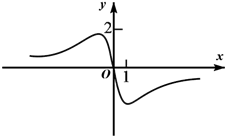 C、
C、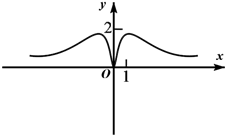 D、
D、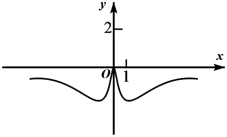 8. 已知函数 在(0,2)上为减函数,则 的取值范围是( )A、(1,3] B、(1,3) C、(0,1) D、[3,+∞)
8. 已知函数 在(0,2)上为减函数,则 的取值范围是( )A、(1,3] B、(1,3) C、(0,1) D、[3,+∞)二、多选题
-
9. 下列命题中,真命题的是( )A、“ ”是“ ”的必要条件 B、 , C、所有圆心角为1弧度的角所对的弧长都相等 D、若 , ,则10. 下列函数存在零点的是( )A、 B、 C、 D、11. 关于函数 ,下面结论正确的是( )A、函数 是奇函数 B、函数 的值域为 C、函数 在R上是增函数 D、函数 在R上是减函数12. 已知定义域为 的函数 ,若对任意 ,存在正数 ,都有 成立,则称函数 是定义域 上的“有界函数”.则下列函数中为“有界函数”的是( )A、 B、 C、 D、
三、填空题
-
13. 的值是.14. 已知幂函数 的图象过点 ,则 .15. 已知一扇形的圆心角为 ,弧长是 ,则扇形的面积是 .16. 定义在R上的偶函数,当 时, ,若不等式 ,则x的取值范围为.
四、解答题
-
17. 已知全集 ,集合 , .(1)、求 , ;(2)、若 ,求实数a的取值范围.18. 已知函数 ,(1)、当 时,求函数 的定义域和值域.(2)、求使 成立的x的取值范围19.(1)、若 ,求 的值;(2)、已知 , ,求 的值.20. 2015年10月,屠呦呦获得诺贝尔生理学或医学奖,理由是她发现了青蒿素,这种药品可以有效降低疟疾患者的死亡率,她成为首获科学类诺贝尔奖的中国人 从青篙中提取的青篙素抗疟性超强,几乎达到 ,据监测:服药后每毫升血液中的含药量 微克 与时间 小时 之间近似满足如图所示的曲线.
 (1)、写出第一次服药后y与t之间的函数关系式 ;(2)、据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
(1)、写出第一次服药后y与t之间的函数关系式 ;(2)、据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?