云南省红河州开远市2021年中考数学一模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、填空题
-
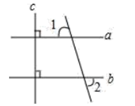
1. 计算: = .2. 因式分解: .3. 如图, , , ,则 .
 4. 若 有意义,则x的取值范围是 .5. 天堑变通途,致富路更宽,农村公路像“毛细血管”一样遍布红河大地,“十三五”以来,红河州共实施农村公路硬化10500千米,人们的幸福感和获得感明显提升.把数据10500用科学记数法表示为 .6. △ABC中, , 为 边上的高, , ,则 的长为 .
4. 若 有意义,则x的取值范围是 .5. 天堑变通途,致富路更宽,农村公路像“毛细血管”一样遍布红河大地,“十三五”以来,红河州共实施农村公路硬化10500千米,人们的幸福感和获得感明显提升.把数据10500用科学记数法表示为 .6. △ABC中, , 为 边上的高, , ,则 的长为 .二、单选题
-
7. 下列体育运动图案中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 8. 如图是由八个相同小正方体组合而成的几何体,其俯视图是( )
8. 如图是由八个相同小正方体组合而成的几何体,其俯视图是( )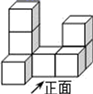 A、
A、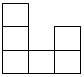 B、
B、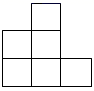 C、
C、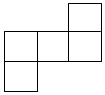 D、
D、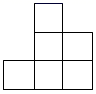 9. 已知下列一组数:1, , , , ,…;用代数式表示第n个数,则第n个数是( )A、 B、 C、 D、10. 已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积是( )A、 B、 C、 D、11. 下列计算正确的是( )A、 B、 C、 D、12. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
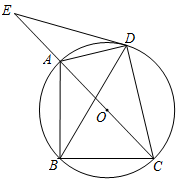
9. 已知下列一组数:1, , , , ,…;用代数式表示第n个数,则第n个数是( )A、 B、 C、 D、10. 已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积是( )A、 B、 C、 D、11. 下列计算正确的是( )A、 B、 C、 D、12. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、13. 如图,是某供水管道的截面图,里面尚有一些水,若液面宽度AB=8cm,半径OC⊥AB于D , 液面深度CD=2cm,则该管道的半径长为( )
A、 B、 C、 D、13. 如图,是某供水管道的截面图,里面尚有一些水,若液面宽度AB=8cm,半径OC⊥AB于D , 液面深度CD=2cm,则该管道的半径长为( )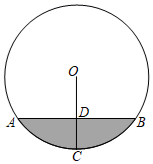 A、6cm B、5.5cm C、5cm D、4cm14. 已知 三边长分别为3、a、7(a为整数),且关于x的不等式组 无解,则满足所有条件的a的和为( )A、17 B、26 C、27 D、30
A、6cm B、5.5cm C、5cm D、4cm14. 已知 三边长分别为3、a、7(a为整数),且关于x的不等式组 无解,则满足所有条件的a的和为( )A、17 B、26 C、27 D、30三、解答题
-
15. 先化简,再求值: 其中16. 如图,AC与BD相交于点O , AB∥CD , OA=OC .
求证:△AOB≌△COD .
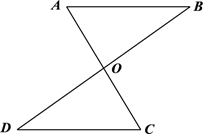 17. 某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
17. 某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: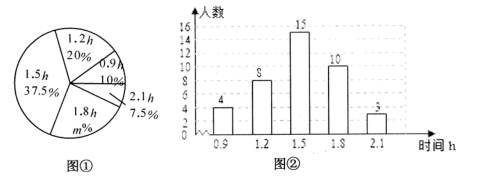 (1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;(3)、根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.18. 城镇老旧小区改造是重大民生工程和发展工程,某县积极响应党的号召,全面推进城区老旧小区改造工作.现计划对城区某小区的居民自来水管道进行改造,该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.这项工程的规定时间是多少天?19. 为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指其他垃圾.小明、小亮各自投放了一袋垃圾.(1)、小明投放的垃圾恰好是C类的概率是;(2)、求小明投放的垃圾与小亮投放的垃圾是同一类的概率.20. 如图,已知一次函数 与反比例函数 的图象相交于点 和 .(1)、求反比例函数与一次函数的解析式;(2)、当反比例函数的值小于一次函数的值时,请直接写出实数 的取值范围;(3)、求△OAB的面积.
(1)、本次接受调查的初中学生人数为 , 图①中m的值为;(2)、求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;(3)、根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.18. 城镇老旧小区改造是重大民生工程和发展工程,某县积极响应党的号召,全面推进城区老旧小区改造工作.现计划对城区某小区的居民自来水管道进行改造,该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.这项工程的规定时间是多少天?19. 为落实“垃圾分类”,环保部门要求垃圾要按A,B,C,D四类分别装袋、投放,其中A类指废电池、过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料、废纸等可回收物,D类指其他垃圾.小明、小亮各自投放了一袋垃圾.(1)、小明投放的垃圾恰好是C类的概率是;(2)、求小明投放的垃圾与小亮投放的垃圾是同一类的概率.20. 如图,已知一次函数 与反比例函数 的图象相交于点 和 .(1)、求反比例函数与一次函数的解析式;(2)、当反比例函数的值小于一次函数的值时,请直接写出实数 的取值范围;(3)、求△OAB的面积. 21. 如图, 的对角线 , 交于点O,过点D作 于E,延长 到点F,使 ,连接 , .
21. 如图, 的对角线 , 交于点O,过点D作 于E,延长 到点F,使 ,连接 , .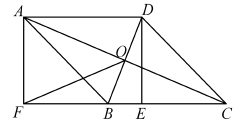 (1)、求证:四边形 是矩形;(2)、若 , , ,试求 的长.
(1)、求证:四边形 是矩形;(2)、若 , , ,试求 的长.