山东省青岛市市南区2021年中考数学二模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 下列四个数中,其绝对值小于2的数是( )A、 B、 C、 D、﹣32. 2021年5月4日享有“最美丽赛道”的青岛马拉松赛圆满举行,近几年马拉松越来越受到运动爱好者的青睐,以下和马拉松相关的图标中既不是轴对称图形也不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 截至5月5日中午,2021年五一档总票房(含预售)突破15.27亿,观影总人次4034.22万,总场次225.31万,打破了五一档票房、人次、场次三项影视记录,15.27亿用科学记数法表示为( )A、 B、 C、 D、4. 一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回,不断重复上述过程.小明共摸了100次,其中80次摸到白球.根据上述数据,小明可估计口袋中的白球大约有( )A、18个 B、15个 C、12个 D、10个5. 下列用数轴表示不等式组 的解集中,正确的是( )A、
3. 截至5月5日中午,2021年五一档总票房(含预售)突破15.27亿,观影总人次4034.22万,总场次225.31万,打破了五一档票房、人次、场次三项影视记录,15.27亿用科学记数法表示为( )A、 B、 C、 D、4. 一个口袋中有3个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回,不断重复上述过程.小明共摸了100次,其中80次摸到白球.根据上述数据,小明可估计口袋中的白球大约有( )A、18个 B、15个 C、12个 D、10个5. 下列用数轴表示不等式组 的解集中,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在平面直角坐标系中,已知点 ,以点 为位似中心,将 缩小为 ,其位似比为2:1,当反比例函数 的图象经过 的中点时, 的值为( )
6. 如图,在平面直角坐标系中,已知点 ,以点 为位似中心,将 缩小为 ,其位似比为2:1,当反比例函数 的图象经过 的中点时, 的值为( )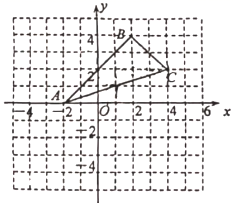 A、 B、2 C、﹣1 D、7. 如图,二次函数 的图象与反比例函数 的图象交于 三点.若 ,则x的取值范围是( )
A、 B、2 C、﹣1 D、7. 如图,二次函数 的图象与反比例函数 的图象交于 三点.若 ,则x的取值范围是( ) A、 B、 或 C、 或 D、 或8. 如图,已知直线 , 之间的距离 为 ,在 中, ,将 绕点 在平面内顺时针旋转得到 ,若旋转角为60°, 交直线 于点 ,则 的长度为( )
A、 B、 或 C、 或 D、 或8. 如图,已知直线 , 之间的距离 为 ,在 中, ,将 绕点 在平面内顺时针旋转得到 ,若旋转角为60°, 交直线 于点 ,则 的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. .10. 如图,点 是 上一点, 是弧 的中点,若 ,则 的度数是°.
 11. 在我国新冠疫情虽然得到了有效的控制,但防范意识仍不能松懈,小丽去药店购买口罩和酒精消毒湿巾,若买150只一次性口罩和10包酒精消毒湿巾,需付75元;若买200只一次性口罩和12包酒精消毒湿巾,需付96元.设一只一次性医用口罩 元,一包酒精消毒湿巾 元,根据题意可列二元一次方程组: .12. 抛物线 与直线 没有交点,则 的取值范围是 .13. 如图,在扇形 中, , 平分 交弧 于点 ,点 为半径 上一动点,若 ,则阴影部分周长的最小值为 .
11. 在我国新冠疫情虽然得到了有效的控制,但防范意识仍不能松懈,小丽去药店购买口罩和酒精消毒湿巾,若买150只一次性口罩和10包酒精消毒湿巾,需付75元;若买200只一次性口罩和12包酒精消毒湿巾,需付96元.设一只一次性医用口罩 元,一包酒精消毒湿巾 元,根据题意可列二元一次方程组: .12. 抛物线 与直线 没有交点,则 的取值范围是 .13. 如图,在扇形 中, , 平分 交弧 于点 ,点 为半径 上一动点,若 ,则阴影部分周长的最小值为 . 14. 如图,正方形 中, ,点 是对角线 上一点,连接 ,过点 作 ,交 于点 ,连接 ,交 于点 ,将 沿 翻折,得到 ,连接 ,交 于点 ,若点 是 边的中点,则线段 的长是 .
14. 如图,正方形 中, ,点 是对角线 上一点,连接 ,过点 作 ,交 于点 ,连接 ,交 于点 ,将 沿 翻折,得到 ,连接 ,交 于点 ,若点 是 边的中点,则线段 的长是 .
三、解答题
-
15. 已知: .求作: ,使圆心 在边 上,并与 的另外两边相切.
 16.(1)、化简: ;(2)、计算: .17. 小明和小刚用如图所示的两个转盘做游戏游戏规则如下:分别旋转两个转盘,将 盘转出的数字作为被减数, 盘转出的数字作为减数;如果差为负数则小刚胜;若差为正数,则小明胜.这个游戏对双方公平吗?请用列表或画树状图的方法说明你的理由.
16.(1)、化简: ;(2)、计算: .17. 小明和小刚用如图所示的两个转盘做游戏游戏规则如下:分别旋转两个转盘,将 盘转出的数字作为被减数, 盘转出的数字作为减数;如果差为负数则小刚胜;若差为正数,则小明胜.这个游戏对双方公平吗?请用列表或画树状图的方法说明你的理由. 18. 《中学生体质健康标准》规定学生体质健康等级标准:90分及以上为优秀;80分﹣89分为良好;60分﹣79分为及格;60分以下为不及格.为了解学生的体质情况,某校从全校九年级学生中随机抽取10%的学生进行测试,并将测试成绩制成如图表:
18. 《中学生体质健康标准》规定学生体质健康等级标准:90分及以上为优秀;80分﹣89分为良好;60分﹣79分为及格;60分以下为不及格.为了解学生的体质情况,某校从全校九年级学生中随机抽取10%的学生进行测试,并将测试成绩制成如图表:成绩
频数
频率
不及格
4
0.08
及格
18
0.36
良好
a
0.24
优秀
16
b
请根据图表中信息解答下列问题:
 (1)、 , ;(2)、已知“ ”这组的数据如下:81,83,84,85,85,81,80,86,87,88,83,85,则所抽取的这些学生测试成绩的中位数是分;(3)、求参加本次测试学生的平均成绩;(4)、请估计全校九年级体质测试成绩为“良好”等级及以上的学生数.19. 如图,EF表示一座风景秀美的观景山,AC,CE是已经修好的登山步行道。该景区为方便老年游客登顶观景,欲在山脚A与山顶E之间架设一条登山索道AE。在山脚A处测得点C的仰角为24°,在C处测得山顶E的仰角为45°,在山脚A处测得山顶E的仰角为37°.已知步行道AC长640米,则新架设的索道AE长多少米?
(1)、 , ;(2)、已知“ ”这组的数据如下:81,83,84,85,85,81,80,86,87,88,83,85,则所抽取的这些学生测试成绩的中位数是分;(3)、求参加本次测试学生的平均成绩;(4)、请估计全校九年级体质测试成绩为“良好”等级及以上的学生数.19. 如图,EF表示一座风景秀美的观景山,AC,CE是已经修好的登山步行道。该景区为方便老年游客登顶观景,欲在山脚A与山顶E之间架设一条登山索道AE。在山脚A处测得点C的仰角为24°,在C处测得山顶E的仰角为45°,在山脚A处测得山顶E的仰角为37°.已知步行道AC长640米,则新架设的索道AE长多少米?(参考数据:sin24°≈ ,cos 24°≈ ,tan24°≈ ,sin37°≈ ,cos37°≈ ,tan 37°≈ )
 20. 端午节是我国历史最为悠久的民间节日之一,也是中国首个入选世界非遗的节日.每年农历五月初五,民间都有“赛龙舟、吃粽子、挂艾草菖蒲”等习俗.为了迎接今年端午节,某加工企业试生产甲、乙两种粽子礼盒试销,每个甲种礼盒所需包装纸的面积比乙种礼盒多0.2平方米.用20平方米包装纸生产甲种礼盒的个数是用同样面积生产乙种礼盒个数的 ,该企业共购进礼盒包装纸900平方米.(1)、每个甲种和乙种礼盒所需包装纸的面积分别是多少?(2)、加工企业拟生产甲种礼盒 个,乙种礼盒 个,刚好用完包装纸,求 关于 的函数关系式;(3)、已知每个甲种礼盒利润是10元、每个乙种礼盒利润是8元,在(2)的前提下,若将两种礼盒全部卖出,该企业要获得21000元总利润,应如何安排甲、乙两种礼盒的生产数量.21. 已知:如图,在 中, , 的平分线交 于点 , 是 的中点,过 作 ,交 的延长线于点 .
20. 端午节是我国历史最为悠久的民间节日之一,也是中国首个入选世界非遗的节日.每年农历五月初五,民间都有“赛龙舟、吃粽子、挂艾草菖蒲”等习俗.为了迎接今年端午节,某加工企业试生产甲、乙两种粽子礼盒试销,每个甲种礼盒所需包装纸的面积比乙种礼盒多0.2平方米.用20平方米包装纸生产甲种礼盒的个数是用同样面积生产乙种礼盒个数的 ,该企业共购进礼盒包装纸900平方米.(1)、每个甲种和乙种礼盒所需包装纸的面积分别是多少?(2)、加工企业拟生产甲种礼盒 个,乙种礼盒 个,刚好用完包装纸,求 关于 的函数关系式;(3)、已知每个甲种礼盒利润是10元、每个乙种礼盒利润是8元,在(2)的前提下,若将两种礼盒全部卖出,该企业要获得21000元总利润,应如何安排甲、乙两种礼盒的生产数量.21. 已知:如图,在 中, , 的平分线交 于点 , 是 的中点,过 作 ,交 的延长线于点 . (1)、求证:四边形 是平行四边形;(2)、 和 满足什么数量关系时,四边形 是菱形.请证明你的结论.22. 正在建设的北京环球影城主题乐园是世界第五个环球影城乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊悚恐怖,但是安全保障措施非常到位.如图所示, 为过山车的一部分轨道,它可以看成一段抛物线.其中 米, 米(轨道厚度忽略不计).
(1)、求证:四边形 是平行四边形;(2)、 和 满足什么数量关系时,四边形 是菱形.请证明你的结论.22. 正在建设的北京环球影城主题乐园是世界第五个环球影城乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊悚恐怖,但是安全保障措施非常到位.如图所示, 为过山车的一部分轨道,它可以看成一段抛物线.其中 米, 米(轨道厚度忽略不计). (1)、求抛物线 的函数关系式;(2)、在轨道距离地面5米处有两个位置 和 ,当过山车运动到 处时,平行于地面向前运动了 米至 点,又进入下坡段 (接口处轨道忽略不计).已知轨道抛物线 的形状与抛物线 完全相同,在 到 的运动过程中,当过山车距地面4米时,它离出发点的水平距离最远有多远?(3)、现需要在轨道下坡段 进行一种安全加固,建造某种材料的水平和竖直支架 ,且要求 .已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?23. 实际问题:有 支队伍,每支队伍都有足够多的水平完全相同的队员,要从这 支队伍中抽调部分队员安排到一张有四个位置的方桌进行竞技比赛,四个位置可以出现来自于同一队伍的队员,为了防止他们作弊,需要避免同队的队员坐在相邻的座位上.那么一共有多少种不同的安排方法?
(1)、求抛物线 的函数关系式;(2)、在轨道距离地面5米处有两个位置 和 ,当过山车运动到 处时,平行于地面向前运动了 米至 点,又进入下坡段 (接口处轨道忽略不计).已知轨道抛物线 的形状与抛物线 完全相同,在 到 的运动过程中,当过山车距地面4米时,它离出发点的水平距离最远有多远?(3)、现需要在轨道下坡段 进行一种安全加固,建造某种材料的水平和竖直支架 ,且要求 .已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?23. 实际问题:有 支队伍,每支队伍都有足够多的水平完全相同的队员,要从这 支队伍中抽调部分队员安排到一张有四个位置的方桌进行竞技比赛,四个位置可以出现来自于同一队伍的队员,为了防止他们作弊,需要避免同队的队员坐在相邻的座位上.那么一共有多少种不同的安排方法?
问题探究:
探究一:如果有两支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设两支队伍分别为 .从①号位开始,我们有2种选择,即 队员或 队员,②③号位置都只有1种选择(另一支队伍的队员).④号位也只有1种选择.这样就得到了 ,一共有两种不同的安排方法.
探究二:如果有三支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
不妨设三支队伍分别为 .让我们运用上面的方法试试①号位置有3种队员可以选择,即 队员、 队员或 队员,②③两个位置选择队员时,我们需要考虑两种不同的情形:
第一种:若②③号位队员来自于同一队伍,则②号位有2种选择,③号只有1种选择,④号位会有2中选择,此时会有 种安排方法;
第二种:若②③号位队员来自于不同的队伍,则②号位有2种选择,③号位只有1种选择,④号位也只有1种选择,此时会有 种安排方法.
把上述两种情况的结果加起来得到12+6=18,一共有18种不同的安排方法.
探究三:如果有四支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?(请按照前面的探究方法,描述如果有四支参赛队伍时,会有多少种结果的推算过程)
归纳探究:如果有 支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有多少种不同的安排方法?
无论有多少支参赛队伍,我们都要考虑两种情况:②③号位队员来自于同一个队伍;②③号位队员来自于不同的队伍.
(1)、如果有 支参赛队伍,①号位有种队员可以选择,②号位有种队员可以选择.(2)、若②③号位队员来自于同一队伍,则③号位只有1种选择,④号位有种选择,这样我们就有种安排方法(结果不需化简);(3)、若②③号位队员来自不同队伍,则③号位有种选择,④号位有种选择,这样我们就有种安排方法.(结果不需化简)(4)、如果有 支队伍参赛,要求相邻的座位不能安排同一队的队员,那么共有种不同的安排方法.(结果不需化简)24. 如图,正方形 的边长为 ,点 是边 的中点,点 是线段 上的动点,并以 的速度从点 向点 移动;点 是对角线 上的动点,以 的速度从点 向点 移动,以 为边,向上作正方形 .点 同时移动,移动时间为 秒( ). (1)、当 为何值时,点 在线段 的垂直平分线上?(2)、正方形 移动时边 与边 交于点 ,是否存在某一时刻 ,使四边形 的面积为 ?(3)、当为 为何值时,点 在 的平分线上?(4)、当 为何值时,点 在边 的延长线上?
(1)、当 为何值时,点 在线段 的垂直平分线上?(2)、正方形 移动时边 与边 交于点 ,是否存在某一时刻 ,使四边形 的面积为 ?(3)、当为 为何值时,点 在 的平分线上?(4)、当 为何值时,点 在边 的延长线上?