辽宁省葫芦岛市兴城市2021年中考数学一模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 在1、﹣1、3、﹣2这四个数中,最大的数是( )A、1 B、﹣1 C、3 D、﹣22. 下列几何体其中左视图是矩形的有( )
 A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 下列调查中,适宜采用全面调查方式的是( )A、调查一批新型节能灯泡的使用寿命 B、调查一批进口灌装饮料的防腐剂情况 C、对某市初中生每天阅读时间的调查 D、对某班学生视力情况的调查5. 不等式组 的解集在数轴上表示为( )A、
A、1个 B、2个 C、3个 D、4个3. 下列运算正确的是( )A、 B、 C、 D、4. 下列调查中,适宜采用全面调查方式的是( )A、调查一批新型节能灯泡的使用寿命 B、调查一批进口灌装饮料的防腐剂情况 C、对某市初中生每天阅读时间的调查 D、对某班学生视力情况的调查5. 不等式组 的解集在数轴上表示为( )A、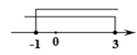 B、
B、 C、
C、 D、
D、 6. 若关于x的方程 有两个相等的实数根,则实数m的值为( )A、-2 B、6 C、-2或6 D、2或-67. 一次函数
6. 若关于x的方程 有两个相等的实数根,则实数m的值为( )A、-2 B、6 C、-2或6 D、2或-67. 一次函数 满足
满足 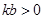 ,且
,且  随
随 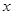 的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图, 是 的直径, 是弦, ,则 的长为( )
的增大而减小,则此函数的图象不经过( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图, 是 的直径, 是弦, ,则 的长为( ) A、 B、 C、 D、9. 如图,在 中, ,分别以 , 为圆心,大于 的长为半径作弧,两弧分别交于点 , ,直线 交 于点 ,交 于点 , , ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, ,分别以 , 为圆心,大于 的长为半径作弧,两弧分别交于点 , ,直线 交 于点 ,交 于点 , , ,则 的长为( ) A、4 B、 C、 D、210. 如图, 中, ,点 为 中点,点 从点 出发,以每秒1个单位长度的速度沿折线 作匀速运动,点 与点 重合时停止运动.设点 的运动时间为 秒, 的面积为 ,则下列图象中能表示 与 的函数关系的图象大致是( )
A、4 B、 C、 D、210. 如图, 中, ,点 为 中点,点 从点 出发,以每秒1个单位长度的速度沿折线 作匀速运动,点 与点 重合时停止运动.设点 的运动时间为 秒, 的面积为 ,则下列图象中能表示 与 的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 新冠病毒直径约为0.00000012米,这个数用科学记数法表示为 .12. 分解因式:2a3﹣8a= .13. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外都相同,其中有5个红球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个黄球的概率为;14. 如图所示,将一副直角三角板按图中所示位置摆放,保持两条斜边互利平行,则 的度数为;
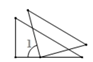 15. 如图,甲,乙两艘船同时从港口 出发,甲船沿北偏东 的方向前进,乙船沿北偏东 方向以每小时30海里的速度前进,两船航行两小时分别到达 , 处,此时测得甲船在乙船的正西方向,则甲船每小时行驶海里;
15. 如图,甲,乙两艘船同时从港口 出发,甲船沿北偏东 的方向前进,乙船沿北偏东 方向以每小时30海里的速度前进,两船航行两小时分别到达 , 处,此时测得甲船在乙船的正西方向,则甲船每小时行驶海里; 16. 如图,正方形 中,将线段 绕点 顺时针旋转 得到线段 , 的延长线交正方形 的对角线 于点 ,则 的度数为;
16. 如图,正方形 中,将线段 绕点 顺时针旋转 得到线段 , 的延长线交正方形 的对角线 于点 ,则 的度数为; 17. 如图,在平面直角坐标系中,点 ,点 从点 出发,在第一象限沿射线 运动,当 是直角三角形时,点 的坐标为 .
17. 如图,在平面直角坐标系中,点 ,点 从点 出发,在第一象限沿射线 运动,当 是直角三角形时,点 的坐标为 . 18. 如图,等边三角形 中, 是 边上的中线,点 在线段 上, , 的延长线交 于点 ,点 在线段 上, ,连接 交 于点 .下面结论:① ;② ;③ ;④ ,其中正确结论的序号为 .
18. 如图,等边三角形 中, 是 边上的中线,点 在线段 上, , 的延长线交 于点 ,点 在线段 上, ,连接 交 于点 .下面结论:① ;② ;③ ;④ ,其中正确结论的序号为 .
三、填空题
-
19. 先化简,再求值 .其中 .20. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .
 (1)、①请作出 绕 点逆时针旋转 的 ;
(1)、①请作出 绕 点逆时针旋转 的 ;②以点 为位似中心,将 扩大为原来的2倍,在 轴的左侧得到 ,请画出 ;
(2)、请直接写出 的正弦值.21. 某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
 (1)、求出样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.22. 如图,一次函数 的图象与 轴交于点 ,与反比例函数 的图象在第一象限交于点 ,过点 作 轴上点 , 的面积为 .
(1)、求出样本容量,并补全直方图;(2)、该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;(3)、已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.22. 如图,一次函数 的图象与 轴交于点 ,与反比例函数 的图象在第一象限交于点 ,过点 作 轴上点 , 的面积为 .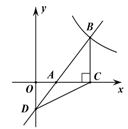 (1)、求反比例函数 的解析式;(2)、求证: 是等腰三角形.23. 如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D , 点O为AB上一点,以O为圆心,AO为半径的圆经过点D .(1)、求证:BC与⊙O相切;(2)、若BD=AD= ,求阴影部分的面积.
(1)、求反比例函数 的解析式;(2)、求证: 是等腰三角形.23. 如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D , 点O为AB上一点,以O为圆心,AO为半径的圆经过点D .(1)、求证:BC与⊙O相切;(2)、若BD=AD= ,求阴影部分的面积. 24. 兴城泳装在国内外享有较高的知名度,网店经销某品牌泳装,每件成本30元,网店按单价不低于成本,且不高于50元销售.在销售过程中发现,泳装每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示.
24. 兴城泳装在国内外享有较高的知名度,网店经销某品牌泳装,每件成本30元,网店按单价不低于成本,且不高于50元销售.在销售过程中发现,泳装每天的销售量 (件)与销售单价 (元)之间满足一次函数关系,其图象如图所示. (1)、求该泳装每天的销售量 (件)与 (元)之间的函数关系式;(2)、当每件泳装的售价为多少元时,每天销售泳装获得的利润为1050元?(3)、销售单价定为多少元时,才能使每天销售泳装获得的利润 (元)最大?最大利润是多少元?25. 如图,在 和 中, , 绕点 旋转.
(1)、求该泳装每天的销售量 (件)与 (元)之间的函数关系式;(2)、当每件泳装的售价为多少元时,每天销售泳装获得的利润为1050元?(3)、销售单价定为多少元时,才能使每天销售泳装获得的利润 (元)最大?最大利润是多少元?25. 如图,在 和 中, , 绕点 旋转.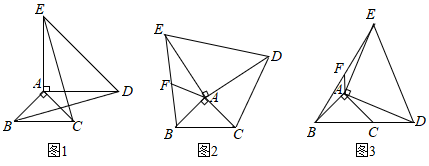 (1)、如图1,若连接 、 ,求证: ;(2)、如图2,若连接 、 ,取 中点 ,连接 ,试探究 与 的数量关系和位置关系,并证明你的结论;(3)、在(2)的条件下,当 旋转到如图3的位置时,点 落在 延长线上,若 ,请直接写出线段 的长.26. 如图,抛物线 与 轴交于 , 两点,其中 , ,与 轴交于点 ,抛物线的对称轴交 轴于点 ,直线 经过点 , ,连接 .
(1)、如图1,若连接 、 ,求证: ;(2)、如图2,若连接 、 ,取 中点 ,连接 ,试探究 与 的数量关系和位置关系,并证明你的结论;(3)、在(2)的条件下,当 旋转到如图3的位置时,点 落在 延长线上,若 ,请直接写出线段 的长.26. 如图,抛物线 与 轴交于 , 两点,其中 , ,与 轴交于点 ,抛物线的对称轴交 轴于点 ,直线 经过点 , ,连接 . (1)、求抛物线和直线 的解析式:(2)、若抛物线上存在一点 ,使 的面积是 面积的2倍,求点 的坐标;(3)、在抛物线的对称轴上是否存在一点 ,使线段 绕 点顺时针旋转 得到线段 ,且 恰好落在抛物线上?若存在,求出点 的坐标;若不存在,请说叫理由.
(1)、求抛物线和直线 的解析式:(2)、若抛物线上存在一点 ,使 的面积是 面积的2倍,求点 的坐标;(3)、在抛物线的对称轴上是否存在一点 ,使线段 绕 点顺时针旋转 得到线段 ,且 恰好落在抛物线上?若存在,求出点 的坐标;若不存在,请说叫理由.