辽宁省葫芦岛市龙港区2021年中考数学一模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 如果 ,那么 的值为( )A、 B、 C、 D、2. 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c , 下列等式中成立的是( )A、 B、 C、 D、3. 如图,以点O为位似中心,把△ABC中放大到原来的2倍得到△A′B′C′.以下说法错误的是( )
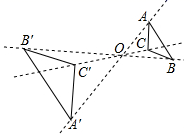 A、△ABC∽△A′B′C′ B、点C , O , C′三点在同一条直线上 C、AB∥A′B′ D、AO:AA′=1:24. 如图是由若干个完全相同的小正方体组合而成的几何体,若将小正方体①移动到小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是( )
A、△ABC∽△A′B′C′ B、点C , O , C′三点在同一条直线上 C、AB∥A′B′ D、AO:AA′=1:24. 如图是由若干个完全相同的小正方体组合而成的几何体,若将小正方体①移动到小正方体②的正上方,下列关于移动后几何体的三视图说法正确的是( )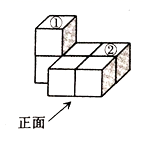 A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、左视图、俯视图和主视图都发生改变5. 如图所示的4个三角形中,相似三角形有( )
A、左视图发生变化 B、俯视图发生变化 C、主视图发生改变 D、左视图、俯视图和主视图都发生改变5. 如图所示的4个三角形中,相似三角形有( )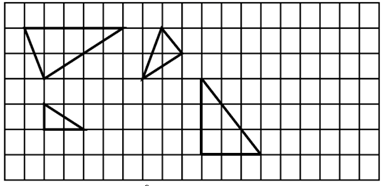 A、1对 B、2对 C、3对 D、4对6. 如图是某河坝横断面示意图, 迎水坡, 为背水坡,过点A作水平面的垂线 ,设斜坡 的坡度为 ,坡角为 ,斜坡 的坡度为 ,坡角为 ,则下列结论正确的是( )
A、1对 B、2对 C、3对 D、4对6. 如图是某河坝横断面示意图, 迎水坡, 为背水坡,过点A作水平面的垂线 ,设斜坡 的坡度为 ,坡角为 ,斜坡 的坡度为 ,坡角为 ,则下列结论正确的是( )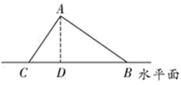 A、 B、 C、 D、7. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )
A、 B、 C、 D、7. 如图,撬钉子的工具是一个杠杆,动力臂 ,阻力臂 ,如果动力F的用力方向始终保持竖直向下,当阻力不变时,则杠杆向下运动时的动力变化情况是( )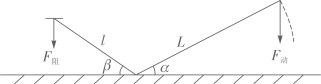 A、越来越小 B、不变 C、越来越大 D、无法确定8. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是
A、越来越小 B、不变 C、越来越大 D、无法确定8. 如图,在平面直角坐标系 中, , , , 是正方形 边上的线段,点 在其中某条线段上,若射线 与 轴正半轴的夹角为 ,且 ,则点 所在的线段可以是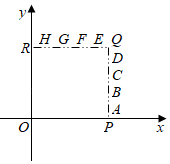 A、 和 B、 和 C、 和 D、 和9. 如图,∠1=∠2,要使△ABC∽△ADE , 只需要添加一个条件即可,这个条件不可能是( )
A、 和 B、 和 C、 和 D、 和9. 如图,∠1=∠2,要使△ABC∽△ADE , 只需要添加一个条件即可,这个条件不可能是( )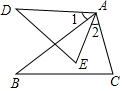 A、∠B=∠D B、∠C=∠E C、 D、10. 正方形 的边长为 ,动点 从 出发,以 的速度沿 向 运动;同时动点 以 的速度沿着 向 运动.如果一个点到达终点,则另一个点也停止运动.设运动时间为 秒, 的面积为 ,则大致反应 与 变化关系的图像是( )
A、∠B=∠D B、∠C=∠E C、 D、10. 正方形 的边长为 ,动点 从 出发,以 的速度沿 向 运动;同时动点 以 的速度沿着 向 运动.如果一个点到达终点,则另一个点也停止运动.设运动时间为 秒, 的面积为 ,则大致反应 与 变化关系的图像是( )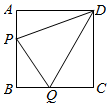 A、
A、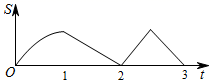 B、
B、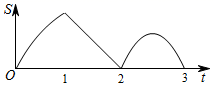 C、
C、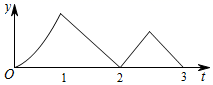 D、
D、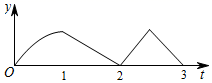
二、填空题
-
11. 两个相似三角形对应角平分线的比为4:3,那么这两个三角形的面积的比是 .12. 在△ABC中,若∠A , ∠B满足|cosA- |+(sinB- )2=0,则∠C= .13. 下图是某个几何体的展开图,该几何体是 .
 14. 如图,在平面直角坐标系中有一点 ,那么 与 轴的正半轴的夹角 的余弦值为 .
14. 如图,在平面直角坐标系中有一点 ,那么 与 轴的正半轴的夹角 的余弦值为 .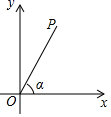 15. 某校初三年级在“停课不停学”期间,积极开展网上答疑活动,在某时间段共开放7个网络教室,其中4个是数学答疑教室,3个是语文答疑教室.为了解初三年级学生的答疑情况,学校教学管理人员随机进入一个网络教室,则该教室是数学答疑教室的概率为 .16. 下列图形中,是中心对称的图形有 .
15. 某校初三年级在“停课不停学”期间,积极开展网上答疑活动,在某时间段共开放7个网络教室,其中4个是数学答疑教室,3个是语文答疑教室.为了解初三年级学生的答疑情况,学校教学管理人员随机进入一个网络教室,则该教室是数学答疑教室的概率为 .16. 下列图形中,是中心对称的图形有 .①正方形;②长方形;③等边三角形;④线段;⑤角;⑥平行四边形.
17. 如图,在▱ABCD中,延长CD至点E , 使DE=DC , 连接BE与AC于点F , 则 的值是 . 18. 如图,在平面直角坐标系中,正方形 与正方形 是以 为位似中心的位似图形,且位似比为,点 , , 在 轴上,延长 交射线 与点 ,以 为边作正方形 ;延长 交射线 与点 ,以 为边作正方形 ;…按照这样的规律继续下去,若 ,则正方形 的面积为 .
18. 如图,在平面直角坐标系中,正方形 与正方形 是以 为位似中心的位似图形,且位似比为,点 , , 在 轴上,延长 交射线 与点 ,以 为边作正方形 ;延长 交射线 与点 ,以 为边作正方形 ;…按照这样的规律继续下去,若 ,则正方形 的面积为 .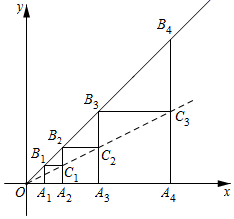
三、解答题
-
19. 先化简,再求值: ,其中 .20. 我市各学校积极响应上级“停课不停教、修课不停学”的要求,开展了空中在线教学.其校就“网络直播课”的满意度进行了随机在线问卷调在,调在结果分为四类: A.非常满意;B.很满意;C.一般;D.不满意,将收集到的信息进行了统计,绘制成如下不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题:(1)、接受问卷调查的学生共有___人; ; ;(2)、补全条形统计图;
频数分布统计表
类别
频数
频率
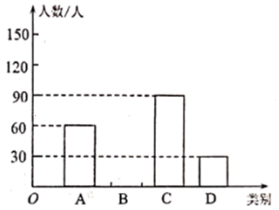 (3)、若该校共有学生 人,请你根据上述调查结果,估计该校对“网络直播课”满意度为 类和 类的学生共有多少人;(4)、为改进教学,学校决定从选填结果是 类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.21. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.
(3)、若该校共有学生 人,请你根据上述调查结果,估计该校对“网络直播课”满意度为 类和 类的学生共有多少人;(4)、为改进教学,学校决定从选填结果是 类的学生中,选取甲、乙、丙、丁四人,随机抽取两名同学参与网络座谈会,求甲、乙两名同学同时被抽中的概率.21. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥 的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥 的长度.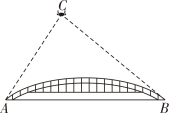
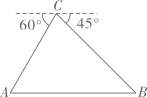 22. 点 是反比例函数 的图象 上一点,直线 轴,交反比例函数 的图象 于点 , 直线 轴,交 于点 , 直线 轴,交 于点 .
22. 点 是反比例函数 的图象 上一点,直线 轴,交反比例函数 的图象 于点 , 直线 轴,交 于点 , 直线 轴,交 于点 . (1)、若点 ,求线段 和 的长度;(2)、对于任意的点 ,判断线段 和 的大小关系,并证明.23. 如图,在 中,点 是 边上一点, , ,过点 的 切 于点 , 平分 .
(1)、若点 ,求线段 和 的长度;(2)、对于任意的点 ,判断线段 和 的大小关系,并证明.23. 如图,在 中,点 是 边上一点, , ,过点 的 切 于点 , 平分 .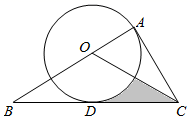 (1)、求证: 是 的切线;(2)、若 ,求 的半径长;(3)、求阴影部分的面积.24. 某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.
(1)、求证: 是 的切线;(2)、若 ,求 的半径长;(3)、求阴影部分的面积.24. 某服装厂生产 品种服装,每件成本为71元,零售商到此服装厂一次性批发 品牌服装 件时,批发单价为 元, 与 之间满足如图所示的函数关系,其中批发件数 为10的正整数倍.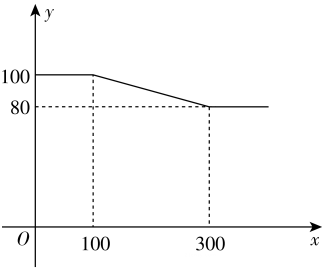 (1)、当 时, 与 的函数关系式为.(2)、某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?(3)、零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?25. 如图,在菱形 中, , 在 边上, 在 的延长线, ,射线 交 于 ,连接 .(1)、如图,当点 是 中点,线段 , , 的数量关系是;
(1)、当 时, 与 的函数关系式为.(2)、某零售商到此服装厂一次性批发 品牌服装200件,需要支付多少元?(3)、零售商到此服装厂一次性批发 品牌服装 件,服装厂的利润为 元,问: 为何值时, 最大?最大值是多少?25. 如图,在菱形 中, , 在 边上, 在 的延长线, ,射线 交 于 ,连接 .(1)、如图,当点 是 中点,线段 , , 的数量关系是; (2)、如图,当点 不是 中点,(1)的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;
(2)、如图,当点 不是 中点,(1)的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;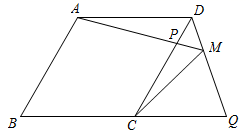 (3)、若 , ,直接写出 的长.26. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,连接 .
(3)、若 , ,直接写出 的长.26. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,连接 .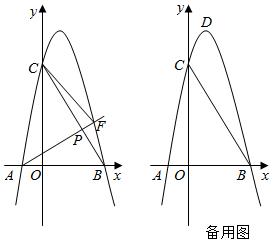 (1)、求抛物线的解析式;(2)、 是线段 上一点,射线 交抛物线于点 .
(1)、求抛物线的解析式;(2)、 是线段 上一点,射线 交抛物线于点 .①连接 , ,若 ,求点 的坐标;
②抛物线的顶点为 ,当 有最小值时,将 沿 轴正方向平移 个单位长度( )得到 ,设 与 重叠部分的面积记为 ,请直接写出 与 的函数关系式.