黑龙江省哈尔滨市南岗区2021年中考数学二模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )A、﹣2 B、 C、﹣ D、22. 下列运算正确的是( )A、a+2a=3a B、(a﹣b)2=a2﹣b2 C、(﹣2a)2=﹣4a2 D、a•2a2=2a23. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
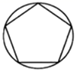 B、
B、 C、
C、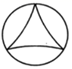 D、
D、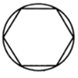 4. 如图是由5个小正方体组合成的几何体,则其俯视图为( )
4. 如图是由5个小正方体组合成的几何体,则其俯视图为( ) A、
A、 B、
B、 C、
C、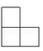 D、
D、 5. 抛物线y=5(x﹣6)2﹣2的顶点坐标是( )A、(6,2) B、(6,﹣2) C、(﹣6,2) D、(﹣6,﹣2)6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( )
5. 抛物线y=5(x﹣6)2﹣2的顶点坐标是( )A、(6,2) B、(6,﹣2) C、(﹣6,2) D、(﹣6,﹣2)6. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、7. 如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为α,测倾仪高AD为1.5米,则铁塔的高BC为( ) A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米8. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、(1.5+150tanα) 米 B、(1.5+ )米 C、(1.5+150sinα)米 D、(1.5+ )米8. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )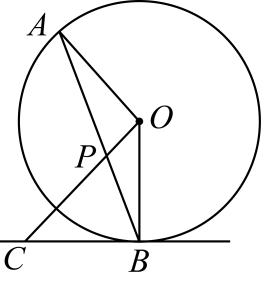 A、 B、 C、 D、9. 如图,点D,E分别在△ABC的边AB,AC上,DE的延长线交BC的延长线于点F,DG∥BC交AC于点G,则下列式子一定正确的是( )
A、 B、 C、 D、9. 如图,点D,E分别在△ABC的边AB,AC上,DE的延长线交BC的延长线于点F,DG∥BC交AC于点G,则下列式子一定正确的是( )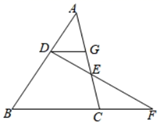 A、 B、 C、 D、10. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,判断下列说法中错误的是( )
A、 B、 C、 D、10. 小明从家步行到学校需走的路程为1800米.图中的折线OAB反映了小明从家步行到学校所走的路程s(米)与时间t(分钟)的函数关系,根据图象提供的信息,判断下列说法中错误的是( )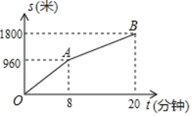 A、小明从家步行到学校共用了20分钟 B、小明从家步行到学校的平均速度是90米/分 C、当t<8时,s与t的函数解析式是s=120t D、小明从家出发去学校步行15分钟时,到学校还需步行360米
A、小明从家步行到学校共用了20分钟 B、小明从家步行到学校的平均速度是90米/分 C、当t<8时,s与t的函数解析式是s=120t D、小明从家出发去学校步行15分钟时,到学校还需步行360米二、填空题
-
11. 2020年5月22日,李克强总理在政府工作报告中指出,农村贫困人口减少11090000人,脱贫攻坚取得决定性成就,把数11090000用科学记数法表示为 .12. 函数 中,自变量 的取值范围是.13. 计算 的结果是 .14. 把多项式 因式分解的结果是.15. 不等式组 的整数解为 .16. 方程 的解为.17. 若一个扇形的弧长为2πcm,面积为2πcm2 , 则这个扇形的半径为cm.18. 某班从甲、乙、丙、丁四位选手中随机选取两人参加校乒乓球比赛,恰好选中甲、乙两位选手的概率是 .19. 在△ABC中,AB=AC,BD是△ABC的高,且BD= AC,则∠C的大小为度.20. 如图,点 是正方形 的中心,点 在 上,连接 ,过点 作 于点 , 分别交 , 于点 , ,若 , ,则 的长为 .
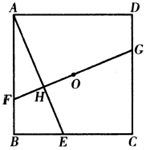
三、解答题
-
21. 先化简,再求代数式(a﹣1+ )÷ 的值,其中a=3tan30°-222. 如图,在7×8的正方形网格中,每个小正方形的边长均为1,有线段AB,点A,B,C均在小正方形的顶点上.
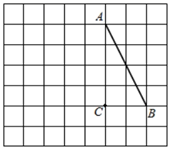 (1)、将线段AB绕着点C逆时针旋转90°得到线段DE(点A,B的对应点分别为点D,E),请画出线段DE;(2)、以AD为对角线作▱AEDF,画出平行四边形AEDF,并直接写出平行四边形AEDF的面积.23. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图:
(1)、将线段AB绕着点C逆时针旋转90°得到线段DE(点A,B的对应点分别为点D,E),请画出线段DE;(2)、以AD为对角线作▱AEDF,画出平行四边形AEDF,并直接写出平行四边形AEDF的面积.23. 我市某学校落实立德树人根本任务,构建“五育并举”教育体系,开设了“厨艺、园艺、电工、木工、编织”五大类劳动课程.为了解七年级学生对每类课程的选择情况,随机抽取了七年级若干名学生进行调查(每人只选一类最喜欢的课程),将调查结果绘制成如图两幅不完整的统计图: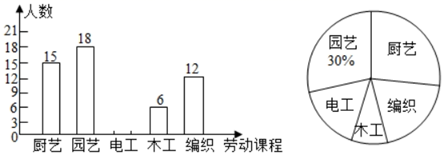 (1)、本次随机调查的学生人数为人;(2)、请通过计算补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“编织”劳动课程的人数.24. 已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.
(1)、本次随机调查的学生人数为人;(2)、请通过计算补全条形统计图;(3)、若该校七年级共有800名学生,请估计该校七年级学生选择“编织”劳动课程的人数.24. 已知:在△ABC中,∠ACB=90°,点D,E分别为BC,AB的中点,连接DE,CE,点F在DE的延长线上,连接AF,且AF=AE.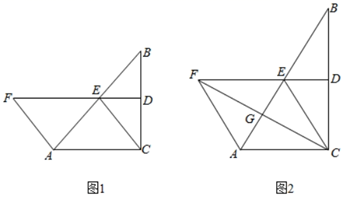 (1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.25. 去年6月以来,我国多地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响,“一方有难,八方支援”,某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区,具体运输情况如下:
(1)、如图1,求证:四边形ACEF是平行四边形;(2)、如图2,当∠B=30°时,连接CF交AB于点G,在不添加任何辅助线的情况下,请直接写出图2中的四条线段,使每条线段的长度都等于线段DE的长度的 倍.25. 去年6月以来,我国多地遭遇强降雨,引发洪涝灾害,人民的生活受到了极大的影响,“一方有难,八方支援”,某市筹集了大量的生活物资,用A,B两种型号的货车,分两批运往受灾严重的地区,具体运输情况如下:第一批
第二批
A型号货车的辆数(单位:辆)
1
2
B型号货车的辆数(单位:辆)
4
5
累计运送货物的吨数(单位:吨)
34
50
备注:第一批、第二批每辆货车均满载
(1)、求A,B两种型号货车每辆满载分别能运多少吨生活物资;(2)、该市后续又筹集了66吨生活物资,现已联系了3辆A型号货车,试问至少还需联系多少辆B型号货车才能一次性将这批生活物资运往目的地.26. 已知:AB与⊙O相切于点B,连接AO交⊙O于点C,延长AO交⊙O于点D,连接BC,BD.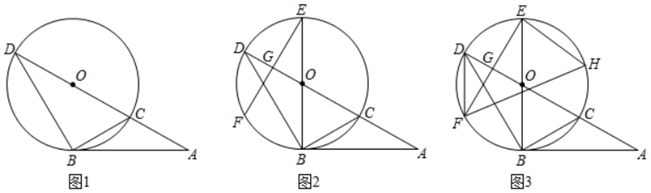 (1)、如图1,求证:∠ABC=∠ADB;(2)、如图2,BE是⊙O的直径,EF是⊙O的弦,EF交OD于点G,并且∠A=∠E,求证: ;(3)、如图3,在(2)的条件下,点H在 上,连接EH,FH,DF,若DF= ,EH=3 ,FH=5 ,求AB的长.27. 如图,在平面直角坐标系中,点 为坐标原点,抛物线 交 轴于 , 两点,已知点 的坐标为(4,0).
(1)、如图1,求证:∠ABC=∠ADB;(2)、如图2,BE是⊙O的直径,EF是⊙O的弦,EF交OD于点G,并且∠A=∠E,求证: ;(3)、如图3,在(2)的条件下,点H在 上,连接EH,FH,DF,若DF= ,EH=3 ,FH=5 ,求AB的长.27. 如图,在平面直角坐标系中,点 为坐标原点,抛物线 交 轴于 , 两点,已知点 的坐标为(4,0).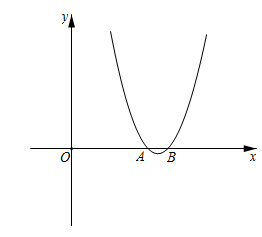 (1)、求抛物线的解析式;(2)、直线 交抛物线于 , 两点(点 在点 左边),点 是抛物线上位于 , 两点之间的一点,过点 作 于点 ,设点 的横坐标为 , 的长为 ,求 与 之间的函数解析式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,连接 , ,点 是线段 上一点,连接 ,当以 , , 为顶点的三角形与 全等时,在直线 上是否存在一点 ,使得 为直角.若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、直线 交抛物线于 , 两点(点 在点 左边),点 是抛物线上位于 , 两点之间的一点,过点 作 于点 ,设点 的横坐标为 , 的长为 ,求 与 之间的函数解析式(不要求写出自变量 的取值范围);(3)、在(2)的条件下,连接 , ,点 是线段 上一点,连接 ,当以 , , 为顶点的三角形与 全等时,在直线 上是否存在一点 ,使得 为直角.若存在,求出点 的坐标;若不存在,请说明理由.