河北省唐山市路南区2021年中考数学二模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 已知 ,则 表示数( )A、 B、 C、2 D、-22. 以下问题,不适合全面调查的是( )A、调查和一新冠肺炎感染者密切接触人群 B、调查我市中学生心理健康现状 C、检测长征运载火箭的零部件质量情况 D、调查某中学在职教师的身体健康状况3. 如图,直线l∥m , 将三角形△ABC(∠ABC=45°)的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
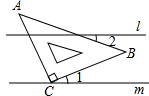 A、20° B、25° C、30° D、35°4. 一个整数81550…0用科学记数法表示为 ,则原数中“0”的个数为( )A、4 B、6 C、7 D、105. 一个多边形的内角和是外角和的2倍,则这个图形是( )A、
A、20° B、25° C、30° D、35°4. 一个整数81550…0用科学记数法表示为 ,则原数中“0”的个数为( )A、4 B、6 C、7 D、105. 一个多边形的内角和是外角和的2倍,则这个图形是( )A、 B、
B、 C、
C、 D、
D、 6. 语句“ 的 与 的和超过2”可以表示为( )A、 B、 C、 D、7. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、
6. 语句“ 的 与 的和超过2”可以表示为( )A、 B、 C、 D、7. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、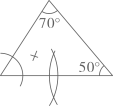 B、
B、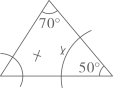 C、
C、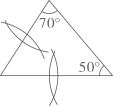 D、
D、 8. 对于 叙述正确的是( )A、 个 相加 B、16个 相加 C、 个16相乘 D、 个16相加9. 如图为大众汽车的图标,是轴对称图形,则下列关于对称轴条数的说法中,正确的是( )
8. 对于 叙述正确的是( )A、 个 相加 B、16个 相加 C、 个16相乘 D、 个16相加9. 如图为大众汽车的图标,是轴对称图形,则下列关于对称轴条数的说法中,正确的是( ) A、有无数条 B、有4条 C、有2条 D、有1条10. 若 为正整数,则计算 的结果是( )A、正整数 B、负整数 C、非负整数 D、非正整数11. 如图是某几何体的三视图及相关数据,则下列结论正确的是( )
A、有无数条 B、有4条 C、有2条 D、有1条10. 若 为正整数,则计算 的结果是( )A、正整数 B、负整数 C、非负整数 D、非正整数11. 如图是某几何体的三视图及相关数据,则下列结论正确的是( ) A、 B、 C、 D、12. 如图,已知动点 , 分别在 轴, 轴正半轴上,动点 在反比例函数 图象上, 轴,当点 的横坐标逐渐增大时, 的面积将会( )
A、 B、 C、 D、12. 如图,已知动点 , 分别在 轴, 轴正半轴上,动点 在反比例函数 图象上, 轴,当点 的横坐标逐渐增大时, 的面积将会( )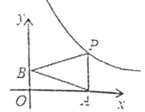 A、越来越小 B、越来越大 C、不变 D、先变大后变小13. 如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A、越来越小 B、越来越大 C、不变 D、先变大后变小13. 如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A′B′的位置,已知AO的长为4米.若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( ) A、 米 B、4sinα米 C、 米 D、4cosα米14. 如图,在 中, , ,三个全等的正方形的对称中心分别是 的顶点,且它们各边与 的两直角边平行或垂直.若正方形的边长为 ,且 ,阴影部分的面积为 ,则能反映 与 之间函数关系的大致图象是( )
A、 米 B、4sinα米 C、 米 D、4cosα米14. 如图,在 中, , ,三个全等的正方形的对称中心分别是 的顶点,且它们各边与 的两直角边平行或垂直.若正方形的边长为 ,且 ,阴影部分的面积为 ,则能反映 与 之间函数关系的大致图象是( )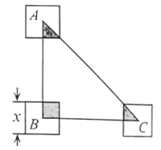 A、
A、 B、
B、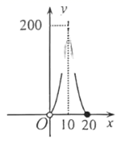 C、
C、 D、
D、 15. 小刚在解关于 的方程 时,只抄对了 , ,解出其中一个根是 .他核对时发现所抄的b比原方程的b值小1,则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有另一个根是 D、有两个相等的实数根16. 将矩形 绕点 顺时针旋转 ,得到矩形 .当 时,下列针对 值的说法正确的是( )
15. 小刚在解关于 的方程 时,只抄对了 , ,解出其中一个根是 .他核对时发现所抄的b比原方程的b值小1,则原方程的根的情况是( )A、不存在实数根 B、有两个不相等的实数根 C、有另一个根是 D、有两个相等的实数根16. 将矩形 绕点 顺时针旋转 ,得到矩形 .当 时,下列针对 值的说法正确的是( ) A、 或 B、 或 C、 D、
A、 或 B、 或 C、 D、二、填空题
-
17. 已知 ,则 .18. 如图所示,以 的顶点 为圆心, 为半径作圆,交 , 于 , ,延长 交 于 ,连结 、 ,当 时, .
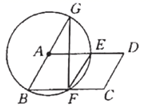 19. 如图,在平面直角坐标系中,已知 ,以线段 为边在第四象限内作等边 ,点 为 正半轴上一动点( ),连接 ,以线段 为边在第四象限内作等边 ,连结 并延长,交 轴于点 .则 ;当以 , , 为顶点的三角形是等腰三角形时,点 的坐标为 .
19. 如图,在平面直角坐标系中,已知 ,以线段 为边在第四象限内作等边 ,点 为 正半轴上一动点( ),连接 ,以线段 为边在第四象限内作等边 ,连结 并延长,交 轴于点 .则 ;当以 , , 为顶点的三角形是等腰三角形时,点 的坐标为 .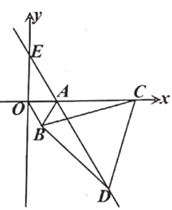
三、解答题
-
20. 如图,数轴上 、 、 三个数所对应的点分别为 、 、 ,已知 , 与 距离2个单位, 与 距离6个单位.
 (1)、①直接写出数 、 的值;
(1)、①直接写出数 、 的值;②求代数式 的值;
(2)、若将数轴折叠,使得点 与点 重合,求与点 重合的点表示的数.21. 小明到某水果店购买苹果和梨,他发现一人购买1千克苹果和2千克梨共花费了26元,另一人购买2千克苹果和1千克梨共花费了22元.(1)、妈妈给小明带了20元钱,想购买1千克苹果和1千克梨;小明带的钱够用吗?说明理由;(2)、到家后妈妈给小明出了一道题:如果给你带100元钱.①当购买苹果和梨的重量相等时,最多能够买多少千克苹果?(千克只取整数)
②当购买苹果的重量是梨的重量的2倍时,最多能够买多少千克苹果?(千克只取整数)
22. 某小区为了改善生态环境,促进生活垃圾的分类处理,将生活垃圾分为三类:厨余、可回收和其他,分别记为 、 、 ,并且设置了相应的垃圾箱,分别贴上“厨余垃圾”、“可回收物”和“其他垃圾”,分别记为 , , .(1)、若将三类垃圾随机投入三类垃圾箱,请用画树状图或列表的方法求垃圾投放正确的概率;(2)、为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共10吨生活垃圾,数据统计如下(单位:吨):3
0.8
1.2
0.24
0.3
2.46
0.32
0.28
1.4
试估计“可回收垃圾”投放正确的概率.
(3)、该小区所在城市每天大约产生500吨生活垃圾,根据以上信息,试估算其中“可回收垃圾”每天投放正确的有多少吨?23. 甲、乙两个工程队同时开始维修某段路面,一段时间后,乙队被调往别处,甲队又用了3小时完成了剩余的维修任务,已知甲队每小时维修路面的长度保持不变,乙队每小时维修路面50米,甲、乙两队在此路段的维修总长度 (米)与维修时间 (时)之间的函数图象如图所示.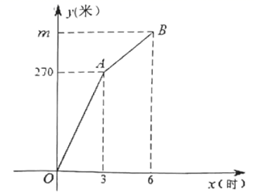 (1)、乙队调离时,甲、乙两队已完成的维修长度为米;(2)、求甲队每小时维修路面多少米?(3)、求乙队调离后 与 之间的函数关系式.24. 如图,在 中, 是直径,点 是 上一点,且 ,过点 作 的切线 交 延长线于点 , 为弧 的中点,连接 、 , 与 交于点 .
(1)、乙队调离时,甲、乙两队已完成的维修长度为米;(2)、求甲队每小时维修路面多少米?(3)、求乙队调离后 与 之间的函数关系式.24. 如图,在 中, 是直径,点 是 上一点,且 ,过点 作 的切线 交 延长线于点 , 为弧 的中点,连接 、 , 与 交于点 . (1)、求证: ;(2)、已知图中阴影部分面积为 .
(1)、求证: ;(2)、已知图中阴影部分面积为 .①求 的半径 ;
②直接写出图中阴影部分的周长.
25. 图中曲线是抛物线的一部分,我们建立如图所示的平面直角坐标系, ,抛物线最高点的坐标为 . (1)、①求图中曲线对应的函数关系式;
(1)、①求图中曲线对应的函数关系式;②求自变量 的取值范围;
(2)、图中曲线与 轴交点的坐标为;(3)、若抛物线形状不变,将其平移后仍过 点,且与 轴正半轴交于点 , ,求平移后抛物线的最大高度是多少?26. 如图,已知在 中, , , .动点 以每秒2个单位的速度,从点 出发,沿着 的方向运动,当点 到达点 时,运动停止.点 是点 的关于点 的对称点,过点 作 于点 ,以 , 为边作 ,设点 的运动时间为 秒.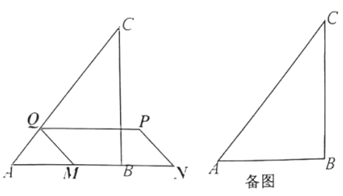 (1)、求 的长;(2)、分别求当 和 时,线段 的长;(3)、是否存在这样的 值,使得 为菱形?若存在,请求出 的值;若不存在,请说明理由;(4)、作点 关于直线 的对称点 ,当点 落在 内部时,请直接写出 的取值范围.
(1)、求 的长;(2)、分别求当 和 时,线段 的长;(3)、是否存在这样的 值,使得 为菱形?若存在,请求出 的值;若不存在,请说明理由;(4)、作点 关于直线 的对称点 ,当点 落在 内部时,请直接写出 的取值范围.