河北省滦州市2021年中考数学二模试卷

试卷更新日期：2021-06-28 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，在平面内过点O作已知直线m的垂线，可作垂线的条数有（）

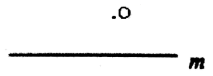A、0条 B、1条 C、2条 D、无数条

查看试题解析
2. 实数a在数轴上的对应点的位置如图所示．若实数 $b$ 满足 $- a < b < a$ ，则b的值可以是（）

A、2 B、-1 C、-2 D、-3

查看试题解析
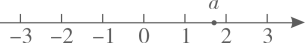3. 对于① $(x + 3) (x - 1) = x^{2} + 2 x - 3$ ，② $x - 3 x y = x (1 - 3 y)$ 从左到右的变形，表述正确的是（）

A、都是因式分解 B、都是整式的乘法 C、①是因式分解，②是整式的乘法 D、①是整式的乘法，②是因式分解

查看试题解析
4. 设面积为7的正方形边长为m，下列关于m的四种说法：①m是无理数；②m可用数轴上的一个点来表示；③3＜m＜4；④m是49的算术平方根，其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 下列算式中，结果等于 $x^{8}$ 的是（）

A、 $x^{2} \cdot x^{2} \cdot x^{2} \cdot x^{2}$ B、 $x^{2} + x^{2} + x^{2} + x^{2}$ C、 $x^{2} \cdot x^{4}$ D、 $x^{6} + x^{2}$

查看试题解析
6. 下面是黑板上出示的尺规作图题，需要回答横线上符号代表的内容．
如图，已知∠AOB，求作：∠DEF，使∠DEF＝∠AOB．

作法：

⑴以△为圆心，任意长为半径画弧，分别交OA，OB于点P，Q；

⑵作射线EG，并以点E为圆心，○长为半径画弧交EG于点D；

⑶以点D为圆心，* 长为半径画弧交前弧于点F；

⑷作⊕，则∠DEF即为所求作的角．

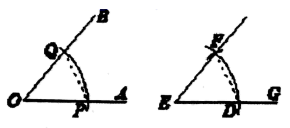A、△表示点E B、○表示PQ C、*表示ED D、⊕表示射线EF

查看试题解析
7. 如图，快艇从 $A$ 地出发，要到距离 $A$ 地10海里的 $C$ 地去，先沿北偏东70°方向走了8海里，到达 $B$ 地，然后再从 $B$ 地走了6海里到达 $C$ 地，此时快艇位于 $B$ 地的（）．

A、北偏东20°方向上 B、北偏西20°方向上 C、北偏西30°方向上 D、北偏西40°方向上

查看试题解析
8. 由7个大小相同的正方体搭成的几何体如图所示，则以下结论：①主视图既是轴对称图形，又是中心对称图形；②俯视图是中心对称图形；③左视图不是中心对称图形；④俯视图和左视图都不是轴对称图形，其中符合题意结论是（）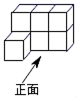

A、①③ B、①④ C、②③ D、②④

查看试题解析
9. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了 $\frac{1}{200000}$ 米，用科学记数法表示 $\frac{1}{200000}$ 为（）

A、 $2 \times 10^{- 5}$ B、 $2 \times 10^{- 6}$ C、 $5 \times 10^{- 5}$ D、 $5 \times 10^{- 6}$

查看试题解析
10. 嘉淇同学进行立定跳远练习，一共练习了7次，将成绩制成如图所示的折线统计图（成绩为整数，满分10分）．若嘉淇同学又跳了一次，成绩恰好是原来7次成绩的中位数，则这8次成绩和原来7次成绩相比（　　）

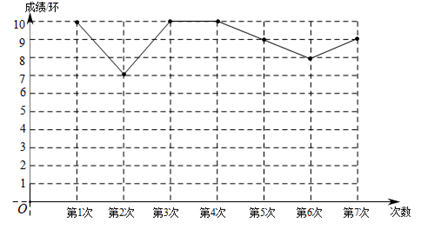A、众数没变，方差变小 B、众数没变，方差变大 C、中位数没变，方差变小 D、中位数没变，方差变大

查看试题解析
11. 化简分式 $\frac{x - 3}{x^{2} - 1} + \frac{3}{1 - x}$ 过程中开始出现错误的步骤是（）
$\frac{x - 3}{x^{2} - 1} + \frac{3}{1 - x} = \frac{x - 3}{(x + 1) (x - 1)} - \frac{3 (x + 1)}{(x + 1) (x - 1)}$ …………①

$= \frac{x - 3 - 3 x + 1}{(x + 1) (x - 1)}$ ………②

$= \frac{- 2 x - 2}{(x + 2) (x - 1)}$ …………③

$= - \frac{2}{x - 1}$ …………④

A、① B、② C、③ D、④

查看试题解析
12. 定义“a*b”：对于任意实数a，b，都有a*b＝（a＋b）（a－b）－1，其中等式右边是通常的加法、减法、乘法运算，若x*k＝x（k为实数）是关于x的方程，则它的根的情况为（）

A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
13. 如图，在同一块矩形草地上，修一条小路（小路任何地方的水平宽度都是1），关于四条小路的面积，下列说法正确的是（）

A、 $S_{1} < S_{2} < S_{3}$ B、 $S_{1} < S_{2} < S_{4}$ C、 $S_{2} = S_{4} < S_{3}$ D、 $S_{1} = S_{3} < S_{4}$

查看试题解析
14. 某种正方形合金板材的成本y（元）与它的面积成正比，设边长为xcm.当x＝3时，y＝18，那么当成本为72元时，边长为（　　）

A、6cm B、12cm C、24cm D、36cm

查看试题解析
15. 如图，现要在抛物线 $y = x (6 - x)$ 上找点 $P (a ， b)$ ；针对b的不同取值，所找点P的个数，三人的说法如下，

甲：若 $b = 15$ ，则点P的个数为0；

乙：若 $b = 9$ ，则点P的个数为1；

丙：若 $b = 3$ ，则点P的个数为1.

下列判断正确的是（　　）

A、乙错，丙对 B、甲和乙都错 C、乙对，丙错 D、甲错，丙对

查看试题解析
16.
如图是甲、乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（　　）

A、甲、乙都可以 B、甲、乙都不可以 C、甲不可以、乙可以 D、甲可以、乙不可以

查看试题解析

二、填空题

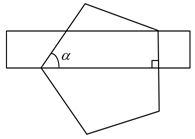
17. 已知： $- \sqrt{50} + \sqrt{\frac{1}{2}} = a \sqrt{2} + b \sqrt{2} = c \sqrt{2}$ ，则ab＋c的值可能是．

查看试题解析
18. 如图，将透明直尺叠放在正五边形之上，若正五边形有两个顶点在直尺的边上，且有一边与直尺的边垂直．则 $∠ α =$ °．

查看试题解析
19. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象G与直线l：y＝2x－4交于点A（3，a）．

(1)、则k＝；

(2)、已知点P（0，n）（n＞0），过点P作平行于x轴的直线，与图象G交于点B，与直线l交于点C．横、纵坐标都是整数的点叫做整点．记图象G在点A，B之间的部分与线段AC，BC围成的区域（不含边界）为W．

①当n＝5时，区域W内的整点个数为；

②若区域W内的整点恰好为3个，则n的取值范围．

查看试题解析

三、解答题

20. 已知“□－7＝△＋3”，其中□和△分别表示一个实数．

(1)、若□表示的数是3，求△表示的数；

(2)、若□和△表示的数互为相反数，求□和△分别表示的数；

(3)、当□和△分别取不同的值时，在□与△的＋，－，×，÷，四种运算中，哪种运算的结果一定不会发生变化，请说明理由．

查看试题解析
21. 如图，约定：上方相邻两数之差等于这两个数下方箭头共同指向的数．示例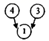：即4－3＝1

(1)、用含x的式子表示m．

(2)、判断n能为负数吗？说明理由．

(3)、当y＝4时，求n的值．

查看试题解析
22. 如图，点B，F，C，E在直线l上，点A，D在l异侧，AB∥DE，AB＝DE，BF＝EC．

(1)、求证：△ABC≌△DEF；

(2)、连接AF、CD，判断四边形AFDC的形状，并说明理由．

查看试题解析
23. 如图，一转盘被等分成四个扇形，上面分别标有1、2、3、4，指针的位置固定不动，自由转动转盘，停止后，记下指针所指扇形上的数（若指针正好停在等分线上，属右边区域）下表是嘉琪转动转盘6次后记录的数据：

次数

1

2

3

4

5

6

数字

3

2

3

4

1

4

(1)、求转动转盘6次后记录的数据的众数；

(2)、求第7次转动转盘后记录的数字是4的概率；

(3)、嘉琪打算继续转动转盘两次，判断是否可能发生这8次记录的数字的平均数不小于3的情况，若有可能，请求出发生此情况的概率，若不可能，请说明理由．

查看试题解析
24. 如图，一次函数y＝kx＋b的图像 $L_{1}$ 与反比例函数 $y = \frac{m}{x}$ 的图像G交于A（－1，n）和B（2，－1），一次函数y＝tx＋4＋3t的图像 $L_{2}$ 与图像G在第二象限交点为p，设P点的横坐标为a（a＜0）．

(1)、求m，k，b的值；

(2)、点D（－3，4）在直线 $L_{1}$ 和 $L_{2}$ 上吗？计算说明理由；

(3)、对于一次函数y＝tx＋4＋3t，当y随x的増大而减小时，直接写出a的取值范围．

查看试题解析
25. 如图，抛物线 $L ： y = \frac{1}{2} (x - t) (x - t + 4)$ （t为常数）与x轴从左到右的交点为B，A，过线段OB的中点M作MP⊥x轴．

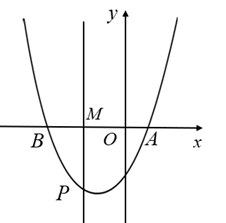(1)、当t＝1时，求AB长，并求直线MP与L对称轴之间的距离；

(2)、当直线MP与L对称轴之间的距离为1时，求t的值；

(3)、把L在直线MP右侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最低点的坐标．

查看试题解析
26. 如图，在平行四边形ABCD中，AB＝10，AD＝15， $\tan A = \frac{4}{3}$ ．点P为AD边上任意一点，连接PB，将PB绕点P逆时针旋转90°得到线段PQ．

(1)、当∠DPQ＝10°时，求∠APB的大小．

(2)、当 $\tan ∠ A B P ： \tan A = 3 ： 2$ 时，求点Q与点B间的距离（结果保留根号）．

(3)、若点Q恰好落在平行四边形ABCD的边所在直线上时，直接写出PB旋转到PQ时点B经过的路径的长（结果保留 $π$ ）．

查看试题解析

次数	1	2	3	4	5	6
数字	3	2	3	4	1	4