广东省汕头市澄海区2021年中考数学模拟试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、6 B、-6 C、 D、2. 全国脱贫攻坚总结表彰大会2021年2月25日上午在北京人民大会堂隆重举行.为如期实现全面脱贫,近几年,国家扶贫资金投入力度持续加大,2020年投入高达1461亿元,其中1461亿用科学记数法表示为( )A、 B、 C、 D、3. 广东省2021年的高考采用“ ”模式:“3”是指语文、数学、外语3科为必选科目,“1”是指在物理、历史2科中任选1科,“2”是指在化学、生物、思想政治、地理4科中任选2科.若小红在“1”中选择了历史,则她在“2”中选地理、生物的概率是( )A、 B、 C、 D、4. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,四边形 是菱形, 、 分别是 、 两边上的点不能保证 和 一定全等的条件是( )
5. 如图,四边形 是菱形, 、 分别是 、 两边上的点不能保证 和 一定全等的条件是( )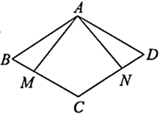 A、 B、 C、 D、6. 如图, 与 相切于点 , 交 于点 ,点 在 上,连接 、 , ,若 ,则 的度数为( )
A、 B、 C、 D、6. 如图, 与 相切于点 , 交 于点 ,点 在 上,连接 、 , ,若 ,则 的度数为( ) A、20° B、25° C、40° D、50°7. 如图,数轴上两点 , 所对应的实数分别为 , ,则 的结果可能是( )
A、20° B、25° C、40° D、50°7. 如图,数轴上两点 , 所对应的实数分别为 , ,则 的结果可能是( ) A、-1 B、0 C、1 D、28. 一列数1,3,7,13,…,按此规律排列,第6个数是( )A、21 B、31 C、43 D、579. 如图,平行于 轴的直线分别交 与 的图象于点 、 ,点 是 轴上的动点,则 的面积为( )
A、-1 B、0 C、1 D、28. 一列数1,3,7,13,…,按此规律排列,第6个数是( )A、21 B、31 C、43 D、579. 如图,平行于 轴的直线分别交 与 的图象于点 、 ,点 是 轴上的动点,则 的面积为( ) A、6 B、4 C、3 D、210. 如图,将四边形纸片 沿过点 的直线折叠,使得点 落在 上的点 处.折痕为 ;再将 , 分别沿 , 折叠,此时点 , 落在 上的同一点 处.下面结论:① 是 的中点;② ;③ ;④当四边形 是平行四边形时, .其中正确的个数为( )
A、6 B、4 C、3 D、210. 如图,将四边形纸片 沿过点 的直线折叠,使得点 落在 上的点 处.折痕为 ;再将 , 分别沿 , 折叠,此时点 , 落在 上的同一点 处.下面结论:① 是 的中点;② ;③ ;④当四边形 是平行四边形时, .其中正确的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 因式分解: .12. 不等式组 的正整数解为 .13. 某校招聘教师,规定综合成绩由笔试成绩和面试成绩构成,其中笔试占60%,面试占40%,有一名应聘者的综合成绩为78分,笔试成绩是80分,则面试成绩为分.14. 一副三角板如图摆放,若 ,则 的度数为 .
 15. 已知 ,则代数式 的值为 .16. 我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是尺.
15. 已知 ,则代数式 的值为 .16. 我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐问水深几何?”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水池里水的深度是尺. 17. 如图,已知 , , ,点 在线段 上, .将 绕点 按顺时针方向旋转30°,使得 与 重合,则线段 经旋转运动所形成的平面图形(即阴影部分)的面积为 .
17. 如图,已知 , , ,点 在线段 上, .将 绕点 按顺时针方向旋转30°,使得 与 重合,则线段 经旋转运动所形成的平面图形(即阴影部分)的面积为 .
三、解答题
-
18. 计算: .19. 化简式子 ,再从-1、0、2中取一个合适的数作为 的值代入求值.20. 如图,在平行四边形 中, .(1)、在 边上确定点 ,使点 到边 , 的距离相等(用尺规作图,不写作法,保留作图痕迹);(2)、在(1)中所作的图形中,若 , ,则 .
 21. 第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小英和小芳分别用5G与4G下载一部900兆的记录片,小英比小芳所用的时间快210秒,求该地4G与5G的下载速度分别是每秒多少兆?22. 疫情期间,某校积极开展“停课不停学”线上教学活动,通过网络进行教学视频推送.为调研学生的线上学习效果,某校随机抽取部分学生进行线上学习效果自我评价调查(学习效果分为:A . 效果很好;B . 效果较好;C . 效果一般;D、效果不理想),并绘制成如下不完整的统计图表.
21. 第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小英和小芳分别用5G与4G下载一部900兆的记录片,小英比小芳所用的时间快210秒,求该地4G与5G的下载速度分别是每秒多少兆?22. 疫情期间,某校积极开展“停课不停学”线上教学活动,通过网络进行教学视频推送.为调研学生的线上学习效果,某校随机抽取部分学生进行线上学习效果自我评价调查(学习效果分为:A . 效果很好;B . 效果较好;C . 效果一般;D、效果不理想),并绘制成如下不完整的统计图表.等级
频数(人数)
频率
A
30%
B
C
20
25%
D
4
5%

请你根据统计图表提供的信息解答下列问题:
(1)、上表中的 , , ;(2)、本次调查共抽取了多少名学生?请补全条形图;(3)、若从D等级的4名学生(两位男生两位女生)中抽取两名学生进行线下辅导,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.23. 如图,在 中, 为 的直径, 为 上一点, 是弧 的中点,过点 作 的垂线,交 的延长线于点 . (1)、求证: 是 的切线;(2)、若 , ,求 的长.24. 将两块全等的三角板如图①摆放,其中 , .
(1)、求证: 是 的切线;(2)、若 , ,求 的长.24. 将两块全等的三角板如图①摆放,其中 , . (1)、将图①中的 顺时针旋转后得到图②,点 是 与 的交点,点 是 与 的交点.若 ,请判断 的形状,并说明理由;(2)、将图①中的 顺时针旋转45°得图③,点 是 与 的交点,点 是 与 的交点,求证: ;(3)、在(2)的条件下,如图④,在 上取一点 ,连接 、 ,设 ,当 时,求 的面积.25. 如图①,抛物线 与 轴负半轴交于点 ,与 轴的另一交点为 ,与 轴正半轴交于点 ,抛物线的对称轴与直线 相交于点 ,与 轴交于点 .
(1)、将图①中的 顺时针旋转后得到图②,点 是 与 的交点,点 是 与 的交点.若 ,请判断 的形状,并说明理由;(2)、将图①中的 顺时针旋转45°得图③,点 是 与 的交点,点 是 与 的交点,求证: ;(3)、在(2)的条件下,如图④,在 上取一点 ,连接 、 ,设 ,当 时,求 的面积.25. 如图①,抛物线 与 轴负半轴交于点 ,与 轴的另一交点为 ,与 轴正半轴交于点 ,抛物线的对称轴与直线 相交于点 ,与 轴交于点 . (1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点 ,使得 ,利用图①求点 的坐标;(3)、如图②,抛物线的对称轴与抛物线相交于点 ,连接 ,在抛物线上是否存在点 (不与点 重合),使得 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点 ,使得 ,利用图①求点 的坐标;(3)、如图②,抛物线的对称轴与抛物线相交于点 ,连接 ,在抛物线上是否存在点 (不与点 重合),使得 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.