2021年高考数学真题试卷（北京卷）

试卷更新日期：2021-06-28 类型：高考真卷

进入出卷网下载

一、选择题共10小题，每小题4分，共40分，在每小题列出的四个选项中，选出符合题目要求的一项．

1. 已知集合 $A = {x | - 1 < x < 1}$ ， $B = {x | 0 \leq x \leq 2}$ ，则 $A \cup B =$ （）

A、 $(- 1, 2)$ B、 $(- 1, 2]$ C、 $[0, 1)$ D、 $[0, 1]$

查看试题解析
2. 在复平面内，复数 $z$ 满足 $(1 - i) z = 2$ ，则 $z =$ （）

A、 $2 + i$ B、 $2 - i$ C、 $1 - i$ D、 $1 + i$

查看试题解析
3. 已知 $f (x)$ 是定义在上 $[0, 1]$ 的函数，那么“函数 $f (x)$ 在 $[0, 1]$ 上单调递增”是“函数 $f (x)$ 在 $[0, 1]$ 上的最大值为 $f (1)$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 某四面体的三视图如图所示，该四面体的表面积为（）

A、 $\frac{3 + \sqrt{3}}{2}$ B、4 C、 $3 + \sqrt{3}$ D、2

查看试题解析
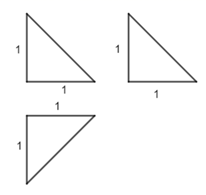5. 双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 过点 $(\sqrt{2}, \sqrt{3})$ ，且离心率为2，则该双曲线的标准方程为（）

A、 $x^{2} - \frac{y^{2}}{3} = 1$ B、 $\frac{x^{2}}{3} - y^{2} = 1$ C、 $x^{2} - \frac{\sqrt{3} y^{2}}{3} = 1$ D、 $\frac{\sqrt{3} x^{2}}{3} - y^{2} = 1$

查看试题解析
6. ${a_{n}}$ 和 ${b_{n}}$ 是两个等差数列，其中 $\frac{a_{k}}{b_{k}} (1 \leq k \leq 5)$ 为常值， $a_{1} = 288$ ， $a_{5} = 96$ ， $b_{1} = 192$ ，则 $b_{3} =$ （）

A、64 B、128 C、256 D、512

查看试题解析
7. 函数 $f (x) = \cos x - \cos 2 x$ ，试判断函数的奇偶性及最大值（）

A、奇函数，最大值为2 B、偶函数，最大值为2 C、奇函数，最大值为 $\frac{9}{8}$ D、偶函数，最大值为 $\frac{9}{8}$

查看试题解析
8. 定义：24小时内降水在平地上积水厚度（ $mm$ ）来判断降雨程度．其中小雨（ $< 10 mm$ ），中雨（ $10 mm - 25 mm$ ），大雨（ $25 mm - 50 mm$ ），暴雨（ $50 mm - 100 mm$ ），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）

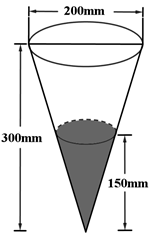A、小雨 B、中雨 C、大雨 D、暴雨

查看试题解析
9. 已知圆 $C : x^{2} + y^{2} = 4$ ，直线 $l : y = k x + m$ ，当 $k$ 变化时， $l$ 截得圆 $C$ 弦长的最小值为2，则 $m =$ （）

A、 $\pm 2$ B、 $\pm \sqrt{2}$ C、 $\pm \sqrt{3}$ D、 $\pm \sqrt{5}$

查看试题解析
10. 数列 ${a_{n}}$ 是递增的整数数列，且 $a_{1} \geq 3$ ， $a_{1} + a_{2} + \cdot \cdot \cdot + a_{n} = 100$ ，则 $n$ 的最大值为（）

A、9 B、10 C、11 D、12

查看试题解析

二、填空题5小题，每小题5分，共25分．

11. ${(x^{3} - \frac{1}{x})}^{4}$ 展开式中常数项为．

查看试题解析
12. 已知抛物线 $C : y^{2} = 4 x$ ，焦点为 $F$ ，点 $M$ 为抛物线 $C$ 上的点，且 $| F M | = 6$ ，则 $M$ 的横坐标是；作 $M N ⊥ x$ 轴于 $N$ ，则 $S_{△ F M N} =$ ．

查看试题解析
13. 若点 $P (\cos θ, \sin θ)$ 与点 $Q (\cos (θ + \frac{π}{6}), \sin (θ + \frac{π}{6}))$ 关于 $y$ 轴对称，写出一个符合题意的 $θ =$ ．

查看试题解析
14. 已知函数 $f (x) = | \lg x | - k x - 2$ ，给出下列四个结论：
①若 $k = 0$ ，则 $f (x)$ 有两个零点；

② $\exists k < 0$ ，使得 $f (x)$ 有一个零点；

③ $\exists k < 0$ ，使得 $f (x)$ 有三个零点；

④ $\exists k > 0$ ，使得 $f (x)$ 有三个零点．

以上正确结论得序号是．

查看试题解析
15. $\vec{a} = (2, 1)$ ， $\vec{b} = (2, - 1)$ ， $\vec{c} = (0, 1)$ ，则 $(\vec{a} + \vec{b}) \cdot \vec{c} =$ ； $\vec{a} \cdot \vec{b} =$ ．

查看试题解析

三、解答题共6小题，共85分，解答应写出文字说明，演算步骤或证明过程．

16. 已知在 $△ A B C$ 中， $c = 2 b \cos B$ ， $C = \frac{2 π}{3}$ ．

(1)、求 $B$ 的大小；

(2)、在下列三个条件中选择一个作为已知，使 $△ A B C$ 存在且唯一确定，并求出 $B C$ 边上的中线的长度．
① $c = \sqrt{2} b$ ；②周长为 $4 + 2 \sqrt{3}$ ；③面积为 $S_{Δ A B C} = \frac{3 \sqrt{3}}{4}$ ；

查看试题解析
17. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，点 $E$ 为 $A_{1} D_{1}$ 中点，直线 $B_{1} C_{1}$ 交平面 $C D E$ 于点 $F$ ．

(1)、证明：点 $F$ 为 $B_{1} C_{1}$ 的中点；

(2)、若点 $M$ 为棱 $A_{1} B_{1}$ 上一点，且二面角 $M - C F - E$ 的余弦值为 $\frac{\sqrt{5}}{3}$ ，求 $\frac{A_{1} M}{A_{1} B_{1}}$ 的值．

查看试题解析
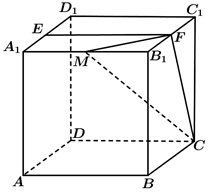18. 为加快新冠肺炎检测效率，某检测机构采取“k合1检测法”，即将k个人的拭子样本合并检测，若为阴性，则可以确定所有样本都是阴性的；若为阳性，则还需要对本组的每个人再做检测．现有100人，已知其中2人感染病毒．

(1)、①若采用“10合1检测法”，且两名患者在同一组，求总检测次数；
②已知10人分成一组，分10组，两名感染患者在同一组的概率为 $\frac{1}{11}$ ，定义随机变量X为总检测次数，求检测次数X的分布列和数学期望E(X)；

(2)、若采用“5合1检测法”，检测次数Y的期望为E(Y)，试比较E(X)和E(Y)的大小(直接写出结果)．

查看试题解析
19. 已知函数 $f (x) = \frac{3 - 2 x}{x^{2} + a}$ ．

(1)、若 $a = 0$ ，求 $y = f (x)$ 在 $(1 ， f (1))$ 处切线方程；

(2)、若函数 $f (x)$ 在 $x = - 1$ 处取得极值，求 $f (x)$ 的单调区间，以及最大值和最小值．

查看试题解析
20. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $A (0 ， - 2)$ ，以四个顶点围成的四边形面积为 $4 \sqrt{5}$ ．

(1)、求椭圆E的标准方程；

(2)、过点P(0，-3)的直线l斜率为k ，交椭圆E于不同的两点B ， C ，直线AB ， AC交y=-3于点M、N ，直线AC交y=-3于点N ，若|PM|+|PN|≤15，求k的取值范围．

查看试题解析
21. 设p为实数．若无穷数列{a_n}满足如下三个性质，则称{a_n}为R_P数列：
：① $a_{1} + p \geq 0$ ， $a_{2} + p = 0$ ；
② $a_{4 n - 1} < a_{4 n} (n = 1 ， 2 ， \dots)$ ；
③ $a_{m + n} \in {a_{m} + a_{n} + p ， a_{m} + a_{n} + p + 1}$ （m=1，2，…；n=1，2，…）．

(1)、如果数列{a_n}的前4项2，-2，-2，-1的数列，那么{a_n}是否可以为 $R_{2}$ 数列？说明理由；

(2)、若数列 ${a_{n}}$ 是 $R_{0}$ 数列，求 $a_{5}$ ；

(3)、设数列{a_n}的前n项和为S_n ，是否存在 $R_{p}$ 数列 ${a_{n}}$ ，对 $S_{n} \geq S_{10}$ 恒成立？若存在，求出所有这样的p；若不存在，说明理由．

查看试题解析