北京市燕山地区2021年中考数学二模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 大兴国际机场,成为北京建设国际化大都市的重要标志.全球唯一一座“双进双出”的航站楼,世界施工技术难度最高的航站楼,走进航站楼内部,室内色调主要以白色为主,为了让阳光洒满整个机场,航站楼一共使用了12800块玻璃,白天室内几乎不需要照明灯光.将12800用科学记数法表示为( )A、1.28×102 B、1.28×103 C、1.28×104 D、1.28×1053. 下列运算正确的是( )A、(a+b)(a﹣b)=a2﹣b2 B、2(2a﹣b)=4a﹣b C、2a+3b=5ab D、(a+b)2=a2+b24. 下列几何体中,是圆柱的为( )A、
2. 大兴国际机场,成为北京建设国际化大都市的重要标志.全球唯一一座“双进双出”的航站楼,世界施工技术难度最高的航站楼,走进航站楼内部,室内色调主要以白色为主,为了让阳光洒满整个机场,航站楼一共使用了12800块玻璃,白天室内几乎不需要照明灯光.将12800用科学记数法表示为( )A、1.28×102 B、1.28×103 C、1.28×104 D、1.28×1053. 下列运算正确的是( )A、(a+b)(a﹣b)=a2﹣b2 B、2(2a﹣b)=4a﹣b C、2a+3b=5ab D、(a+b)2=a2+b24. 下列几何体中,是圆柱的为( )A、 B、
B、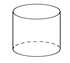 C、
C、 D、
D、 5. 四边形的内角和为( )A、180° B、360° C、540° D、720°6. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( )
5. 四边形的内角和为( )A、180° B、360° C、540° D、720°6. 如图,在Rt△ABC中,∠C=90°, AC=3,BC=4,则sinA的值为( ) A、 B、 C、 D、7. 若a+b-1=0,则代数式 的值为( )A、3 B、-1 C、1 D、-38. 如图,小聪要在抛物线y =x(2-x)上找一点M(a,b),针对b的不同取值,所找点M的个数,三个同学的说法如下,
A、 B、 C、 D、7. 若a+b-1=0,则代数式 的值为( )A、3 B、-1 C、1 D、-38. 如图,小聪要在抛物线y =x(2-x)上找一点M(a,b),针对b的不同取值,所找点M的个数,三个同学的说法如下,小明:若b=-3,则点M的个数为0;
小云:若b = 1,则点M的个数为1;
小朵:若b = 3,则点M的个数为2.
下列判断正确的是( ).
 A、小云错,小朵对 B、小明,小云都错 C、小云对,小朵错 D、小明错,小朵对
A、小云错,小朵对 B、小明,小云都错 C、小云对,小朵错 D、小明错,小朵对二、填空题
-
9. 如图,该正方体的主视图是形.
 10. 如图所示的正方形网格中有 ,则 的值为 .
10. 如图所示的正方形网格中有 ,则 的值为 . 11. 请你写出一个函数,使得当自变量 时,函数 随 的增大而增大,这个函数的解析式可以是 .12. 用四个不等式①a>b,②a +b>2b,③a>0,④a2>ab中的两个不等式作为题设,余下的两个不等式中选择一个作为结论,组成一个真命题: .13. 如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为 .
11. 请你写出一个函数,使得当自变量 时,函数 随 的增大而增大,这个函数的解析式可以是 .12. 用四个不等式①a>b,②a +b>2b,③a>0,④a2>ab中的两个不等式作为题设,余下的两个不等式中选择一个作为结论,组成一个真命题: .13. 如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为 . 14. 如图,小亮从一盏9米高的路灯下 处向前走了 米到达点 处时,发现自己在地面上的影子CE是 米,则小亮的身高DC为米.
14. 如图,小亮从一盏9米高的路灯下 处向前走了 米到达点 处时,发现自己在地面上的影子CE是 米,则小亮的身高DC为米. 15. 如图是房山区行政规划图.如果周口店的坐标是(-2,1),阎村的坐标是(0,2),那么燕山的坐标是 , 窦店坐标是 .
15. 如图是房山区行政规划图.如果周口店的坐标是(-2,1),阎村的坐标是(0,2),那么燕山的坐标是 , 窦店坐标是 . 16. 在就地过年倡议下,更多游客缩小出游半径,本地游、近郊游、周边游取代异地长线游,成为牛年出行新趋势.某地区对近郊游的住宿环境、餐饮、服务等方面对所住游客进行了综合满意度调查,在甲,乙两个景点都去过的的游客中随机抽取了100人,每人分别对这两个景点进行了评分,统计如下:
16. 在就地过年倡议下,更多游客缩小出游半径,本地游、近郊游、周边游取代异地长线游,成为牛年出行新趋势.某地区对近郊游的住宿环境、餐饮、服务等方面对所住游客进行了综合满意度调查,在甲,乙两个景点都去过的的游客中随机抽取了100人,每人分别对这两个景点进行了评分,统计如下:
非常满意
较满意
一般
不太满意
非常不满意
合计
甲
28
40
10
10
12
100
乙
25
20
45
6
4
100
若小聪要在甲,乙两个景点中选择一个景点,根据表格中数据,你建议她去景点(填甲或乙),理由是 .
三、解答题
-
17. 计算: .18. 解不等式组:19. 已知关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、请你给出一个 的值,并求出此时方程的根.20. 下面是小玲同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:如图1,直线l和直线l外一点P.
求作:直线PM,使直线PM∥直线l.

图1
作法:如图2,
①在直线l 上任取一点A,作射线AP;
②以P为圆心,PA为半径作弧,交直线l于点B,连接PB;
③以P为圆心,PB长为半径作弧,交射线AP于点 C;分别以B,C为圆心,大于 长为半径作弧,在AC的右侧两弧交于点M;
④作直线PM;
所以直线PM就是所求作的直线.

图2
根据上述作图过程,回答问题:
(1)、用直尺和圆规,补全图2中的图形;(2)、完成下面的证明:证明:由作图可知PM平分∠CPB,
∴∠CPM =∠ ▲ = ∠CPB.
又∵PA=PB,
∴∠PAB =∠PBA.( ▲ )(填依据).
∵∠CPB=∠PAB +∠PBA,
∴∠PAB =∠PBA = ∠CPB.
∴∠CPM =∠PAB.
∴直线PM∥直线l.( ▲ )(填依据).
21. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第七卷《盈不足》记载了一道有趣的数学问题:“今有大器五、小器一容三斛;大器-、小器五容二斛.向大、小器各容几何?”译文:“今有大容器 个,小容器 个,总容量为 斛;大容器 个,小容器 个,总容量为 斛.向大容器、小容器的容积各是多少斛?”
 22. 某校初三年级有400名学生,为了解学生对代数和几何两部分知识的掌握情况,数学教师对九年级全体学生进行了一次摸底测试,代数和几何满分各50分.现随机抽取20名学生的成绩(成绩均为整数)进行收集、整理、描述和分析,下面给出了部分信息:
22. 某校初三年级有400名学生,为了解学生对代数和几何两部分知识的掌握情况,数学教师对九年级全体学生进行了一次摸底测试,代数和几何满分各50分.现随机抽取20名学生的成绩(成绩均为整数)进行收集、整理、描述和分析,下面给出了部分信息:
c.代数测试成绩在30≤x≤40这一组的数据是:35, 36, 37, 37, 38, 38, 39, 39, 39,39.
d.几何测试成绩在40≤x≤50的数据是40,42,47,47
e.两次成绩的平均数、中位数、众数如下:
平均数
中位数
众数
代数成绩
35.2
n
39
几何成绩
32.05
35.5
37
请根据以上信息,回答下列问题:
(1)、m = , n =;(2)、测试成绩大于或等于30分为及格,测试成绩大于或等于43分为优秀.20名学生的成绩中代数测试及格有人,几何测试优秀有人,估计该校初三年级本次代数测试约有人及格, 几何成绩优秀约有人.(3)、下列推断合理的是 .①代数测试成绩的平均分高于几何的平均分,所以大多数学生代数掌握的比几何好.
②被抽测的学生小莉的几何成绩是29分,她觉得年级里大概有240人的测试成绩比她高,所以她决定迎头赶上.
23. 如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE BC,连接DE,CF. (1)、求证:四边形CEDF是平行四边形;(2)、若AB=4,AD=6,∠A=120°,求△DCE的底边CE上的高及DE的长.24. 如图,A、B两点在函数 的图象上.
(1)、求证:四边形CEDF是平行四边形;(2)、若AB=4,AD=6,∠A=120°,求△DCE的底边CE上的高及DE的长.24. 如图,A、B两点在函数 的图象上. (1)、求 的值及直线AB的解析式;(2)、如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出函数 的图象与直线AB围出的封闭图形中(不包括边界)所含格点的坐标.25. 如图,AB为⊙O的直径,DE为⊙O的切线,点D是AC中点.
(1)、求 的值及直线AB的解析式;(2)、如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出函数 的图象与直线AB围出的封闭图形中(不包括边界)所含格点的坐标.25. 如图,AB为⊙O的直径,DE为⊙O的切线,点D是AC中点. (1)、求证:DE⊥BC;(2)、如果DE=2,tanC= ,求⊙O的半径.26. 在平面直角坐标系 中,抛物线 ( ).
(1)、求证:DE⊥BC;(2)、如果DE=2,tanC= ,求⊙O的半径.26. 在平面直角坐标系 中,抛物线 ( ).

备用图
(1)、求抛物线的对称轴及抛物线与y轴交点坐标.(2)、已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.27. 在等腰三角形ABC中, , .点P是 内一动点,连接AP,BP,将△APB绕点 逆时针旋转 ,使 边与 重合,得到△ADC,射线BP与CD或CD延长线交于点 (点 与点D不重合). (1)、依题意补全图1和图2;由作图知,∠BAP与∠CAD的数量关系为;(2)、探究 与∠APM的数量关系为;(3)、如图1,若DP平分∠ADC,用等式表示线段BM,AP,CD之间的数量关系,并证明.28. 对于平面内的图形G1和图形G2 , 记平面内一点P到图形G1上各点的最短距离为d1 , 点P到图形G2上各点的最短距离为d2 , 若d1=d2 , 就称点P是图形G1和图形G2的一个“等距点”.在平面直角坐标系 xOy 中,已知点 A(6,0),B(0, ).(1)、在C(4,0),D(2,0),E(1,3)三点中,点A和点B的等距点是;(2)、已知直线 y=2.
(1)、依题意补全图1和图2;由作图知,∠BAP与∠CAD的数量关系为;(2)、探究 与∠APM的数量关系为;(3)、如图1,若DP平分∠ADC,用等式表示线段BM,AP,CD之间的数量关系,并证明.28. 对于平面内的图形G1和图形G2 , 记平面内一点P到图形G1上各点的最短距离为d1 , 点P到图形G2上各点的最短距离为d2 , 若d1=d2 , 就称点P是图形G1和图形G2的一个“等距点”.在平面直角坐标系 xOy 中,已知点 A(6,0),B(0, ).(1)、在C(4,0),D(2,0),E(1,3)三点中,点A和点B的等距点是;(2)、已知直线 y=2.①若点A和直线y=2的等距点在x轴上,则该等距点的坐标为 ▲ ;
②若直线y=b上存在点A和直线y=2的等距点,求实数b的取值范围;
(3)、记直线AB为直线l1 , 直线l2: ,以原点O为圆心作半径为r的⊙O.若⊙O上有m个直线l1和直线l2的等距点,以及n个直线l1和y轴的等距点(m≠0,n≠0),当 m≠n 时,求r的取值范围.