2021年浙江省宁波市中考数学模拟试卷（一）

试卷更新日期：2021-06-28 类型：中考模拟

进入出卷网下载

一、单选题

1. $| - \frac{1}{2020} |$ 的值是（）

A、2020 B、－2020 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 下列运算正确的是（）

A、a+a＝a² B、（ab）²＝ab² C、a²•a³＝a⁵ D、（a²）³＝a⁵

查看试题解析
3. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若 $\underset{n 个}{\underset{︸}{0.00 \dots \dots 018}}$ 用科学记数法表示为 $1.8 \times 10^{- 10}$ ，则n的值是（）

A、9 B、10 C、11 D、12

查看试题解析
5. 书架上摆放有5本书，其中2本教科书，3本文学书，任意从书架上抽取1本，抽到教科书的概率是（）

A、 $\frac{1}{7}$ B、 $\frac{1}{2}$ C、 $\frac{2}{5}$ D、 $\frac{1}{3}$

查看试题解析
6. 已知反比例函数的解析式为y＝ $\frac{3 a - 3}{x}$ ，且图象位于第一、三象限，则a的取值范围是（）

A、a＝1 B、a≠1 C、a＞1 D、a＜1

查看试题解析
7. 某市高新区某厂今年新招聘一批员工，他们中不同文化程度的人数见下表，关于这组文化程度的人数数据，以下说法正确的是（）

文化程度

高中

大专

本科

硕士

博士

人数

9

17

20

9

5

A、众数是20 B、中位数是17 C、平均数是12 D、方差是26

查看试题解析
8. 如图，在长方形ABCD中，AE平分∠BAD交BC于点E，连接ED，若ED＝5，EC＝3，则长方形的周长为（）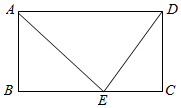

A、20 B、22 C、24 D、26

查看试题解析
9. 已知抛物线y＝ax²﹣2ax＋a﹣c（a≠0）与y轴的正半轴相交，直线AB∥x轴，且与该抛物线相交于A（x₁ ， y₁）B（x₂ ， y₂）两点，当x＝x₁＋x₂时，函数值为p；当x＝ $\frac{x_{1} + x_{2}}{2}$ 时，函数值为q.则p﹣q的值为（）

A、a B、c C、﹣a＋c D、a﹣c

查看试题解析
10. 把六张形状大小完全相同的小长方形卡片（如图①），分两种不同形式不重叠的放在一个长方形盒子底部（如图②、图③），盒子底面未被卡片覆盖的部分用阴影表示，设图②是长方形盒子的周长为C₁ ，阴影部分图形的周长为l₁ ，图③中长方形盒子的周长为C₂ ，阴影部分图形的周长为l₂ ，若C₁﹣C₂＝2，则l₁ ， l₂满足（）

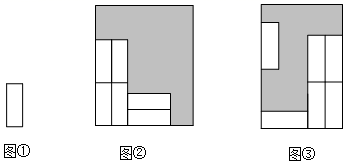A、l₁＝l₂ B、l₁﹣l₂＝1 C、l₁﹣l₂＝2 D、l₁﹣l₂＝4

查看试题解析

二、填空题

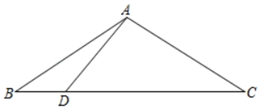
11. 若 $x^{2} + 2 (3 - m) x + 25$ 可以用完全平方式来分解因式，则 $m$ 的值为．

查看试题解析
12. 若代数式 $\sqrt{3 - 2 x}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
13. 已知圆锥的底面半径为 $1 c m$ ，高为 $\sqrt{3} c m$ ，则它的侧面展开图的面积为=.

查看试题解析
14. 如图，△ABC中，AB＝AC，AD＝2，BD•DC＝2 $\sqrt{3}$ ，则AC＝.

查看试题解析
15. 如图，等边三角形ABC的边长为4，E、F分别是边AB，BC上的动点，且AE＝BF，连接EF，以EF为直径作圆O.当圆O与AC边相切时，AE的长为.

查看试题解析
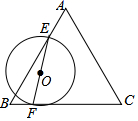16. 如图，平面直角坐标系xOy中，在反比例函数 $y = \frac{4 k}{x}$ （k＞0，x＞0）的图象上取点A，连接OA，与 $y = \frac{k}{x}$ 的图象交于点B，过点B作BC∥x轴交函数 $y = \frac{4 k}{x}$ 的图象于点C，过点C作CE∥y轴交函数 $y = \frac{k}{x}$ 的图象于点E，连接AC，OC，BE，OC与BE交于点F，则 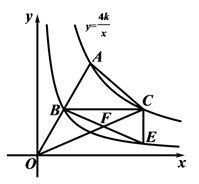$\frac{S_{Δ C E F}}{S_{Δ A B C}}$ ＝.

查看试题解析

三、解答题

17. 计算：6sin45°+|2 $\sqrt{2}$ ﹣7|﹣（ $\frac{1}{2}$ ）³+（2020﹣ $\sqrt{2020}$ ）⁰

查看试题解析
18. 图①、图②、图③都是 $2 \times 2$ 的正方形网格，每个小正方形的顶点称为格点.按下列要求画图：在图①、图②、图③中各画一个以格点为顶点的三角形，要求所画三角形是图中三角形经过轴对称变换后得到的图形，并将所画三角形涂上阴影.(注：所画三角形不能重复)

查看试题解析

19. 为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动.以下是根据调查结果绘制的统计图表的一部分，最喜欢球类运动统计表最喜欢球类运动扇形统计，

类别	A	B	C	D	E	F
类型	足球	羽毛球	乒乓球	篮球	排球	其他
人数		10	4		6	2

根据以上信息，解答下列问题：

(1)、本次共查了名学生；

(2)、统计表中类别D的人数为人，扇形统计图中类别A的扇形圆心角为°；

(3)、该校共有450名学生，根据调查结果，估计该校最喜欢排球的学生数.

查看试题解析

20. 如图，建在山腰点 $A$ 处的一座“5G”发射塔 $A B$ 与地面 $C M$ 垂直，在地面 $C$ 处测得发射塔 $A B$ 的底部 $A$ 、顶端 $B$ 的仰角分别为30°、60°，在地面 $D$ 处测得发射塔 $A B$ 的底部 $A$ 的仰角为45°.

(1)、若设 $A C = k$ ，则 $A D =$ ；（用含 $k$ 的代数式表示）

(2)、若测得 $C D = (18 \sqrt{3} - 18)$ 米，求 $A B$ .

查看试题解析
21. 已知二次函数 $y_{1} = x^{2} + b x - 3$ 的图象与直线 $y_{2} = x + 1$ 交于点 $A (- 1 ， 0)$ 、点 $C (4 ， m)$ .

(1)、求 $y_{1}$ 的表达式和 $m$ 的值；

(2)、当 $y_{1} > y_{2}$ 时，求自变量 $x$ 的取值范围；

(3)、将直线 $A C$ 沿 $y$ 轴上下平移，当平移后的直线与抛物线只有一个公共点时，求平移后的直线表达式.

查看试题解析
22. 甲、乙两人分别从公园长廊在同一直线上的A、B两地同时出发，相向匀速慢跑，甲以6m/s的速度慢跑到B地后，立即按原速返回，乙在第一次相遇后将速度提高到原来的1.5倍，之后匀速慢跑到A地，且乙到达A地后立即以提速后的速度返回，直到两人再次相遇时停止.甲、乙两人之间的路程y（m）与慢跑时间x（s）之间的函数图象如图所示.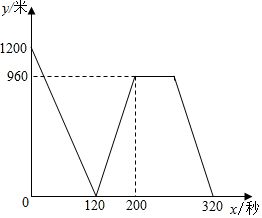

(1)、乙在两人第一次相遇前的速度为m/s，乙到A地的时间为s.

(2)、求乙从A地返回B地时y与x之间的函数关系式，并写出自变量x的取值范围.

(3)、直接写出两次相遇时乙距出发地的路程.

查看试题解析
23. 如图

(1)、如图1，在正 $△ A B C$ 的外角 $∠ C A H$ 内引射线 $A M$ ，作点C关于 $A M$ 的对称点E（点E在 $∠ C A H$ 内），连接 $B E$ ， $B E$ 、 $C E$ 分别交 $A M$ 于点F，G.则 $∠ F E G =$ $°$ .

(2)、类比探究：如图2，把上题中的“正 $△ A B C$ ”改为“正方形 $A B D C$ ”，其余条件不变，请求出 $∠ F E G$ 的度数；通过以上两例探索，请写出一个关于 $∠ F E G$ 与 $∠ B A C$ 的数量关系的正确结论：；

(3)、拓展延伸：如图3，若以正方形 $A O D C$ 的顶点O为原点，顶点A，D分别在x轴，y轴上，点A的坐标为 $(4 ， 0)$ ，设正方形 $A O D C$ 的中心为P，平面上一点F到P的距离为 $2 \sqrt{2}$ .
①直接写出 $∠ O F A$ 的度数；

②当 $S_{△ F A O} = 6$ 时，求点F的坐标；并探索 $S_{△ F A O}$ 是否有最大值？如果有，请求出；如果没有，请说明理由.

查看试题解析
24. 如图，已知AB是⊙O的直径，弦CD⊥AB于点E.点P是劣弧 $\overset{⌢}{A D}$ 上任一点（不与点A，D重合），CP交AB于点M，AP与CD的延长相交于点F.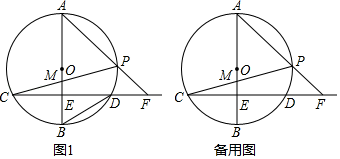

(1)、设∠CPF＝α，∠BDC＝β，求证：α＝β+90°；

(2)、若OE＝BE，设tan∠AFC＝x， $\frac{A M}{B M} = y$ .①求∠APC的度数；
②求y关于x的函数表达式及自变量x的取值范围.

查看试题解析

文化程度	高中	大专	本科	硕士	博士
人数	9	17	20	9	5