浙江省湖州市南浔区2021年数学中考二模试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. -4的倒数是( ).A、 B、 C、-4 D、42. 计算 正确的结果是( ).A、4 B、 C、 D、3. 如图摆放的下列几何体中,左视图是圆的是( ).A、长方体
 B、圆柱体
B、圆柱体  C、圆锥体
C、圆锥体  D、球体
D、球体  4. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数为奇数的概率是( ).A、 B、 C、 D、15. 已知 ,则 的补角是( ).A、 B、 C、 D、6. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )
4. 有一枚均匀的正方体骰子,骰子各个面上的点数分别为1,2,3,4,5,6,若任意抛掷一次骰子,朝上的面的点数为奇数的概率是( ).A、 B、 C、 D、15. 已知 ,则 的补角是( ).A、 B、 C、 D、6. 实数a在数轴上的对应点的位置如图所示.若实数 满足 ,则b的值可以是( )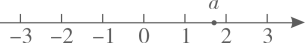 A、2 B、-1 C、-2 D、-37. 母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )A、3种 B、4种 C、5种 D、6种8. 在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(﹣3,﹣6) B、(1,﹣4) C、(1,﹣6) D、(﹣3,﹣4)9. 如图,在四边形 中, , , , , ,点 是 的中点,则 的长为( ).
A、2 B、-1 C、-2 D、-37. 母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )A、3种 B、4种 C、5种 D、6种8. 在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(﹣3,﹣6) B、(1,﹣4) C、(1,﹣6) D、(﹣3,﹣4)9. 如图,在四边形 中, , , , , ,点 是 的中点,则 的长为( ).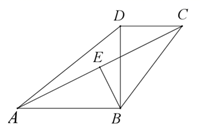 A、2 B、 C、 D、310. 沪苏湖高铁在紧张施工中,现在南浔站已开始隧道挖掘作业,如图1,圆弧形混凝土管片是构成圆形隧道的重要部件,如图2,有一圆弧形混凝土管片放置在水平地面上,底部用两个完全相同的长方体木块固定,为估计隧洞开挖面的大小,甲、乙、丙三个小组对相关数据进行测量方案如下表,利用数据能够估算隧道外径大小的小组有( )
A、2 B、 C、 D、310. 沪苏湖高铁在紧张施工中,现在南浔站已开始隧道挖掘作业,如图1,圆弧形混凝土管片是构成圆形隧道的重要部件,如图2,有一圆弧形混凝土管片放置在水平地面上,底部用两个完全相同的长方体木块固定,为估计隧洞开挖面的大小,甲、乙、丙三个小组对相关数据进行测量方案如下表,利用数据能够估算隧道外径大小的小组有( )小组
测量内容
甲
, 的长
乙
, , 的长
丙
的长,点 、 间距离,点 、 间的距离
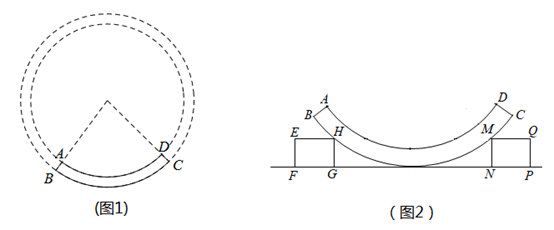 A、三组测量数据都不足 B、一个小组 C、两个小组 D、三个组都可以
A、三组测量数据都不足 B、一个小组 C、两个小组 D、三个组都可以二、填空题
-
11. .12. 某校在开展“迎建党百年,争劳动模范”活动中,一合作学习小组6名同学一周在家劳动的时间(单位: ),分别为:4,4,5,5,5,6.这组数据的众数是.13. 已知圆锥的底面半径为2cm,母线长为6cm,则这个圆锥的展开图圆心角为度.14. 如图,▱ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 .
 15. 对某一个函数给出如下定义:若存在实数 ,对于任意的函数值 ,都满足 ,则称这个函数是有界函数 , 在所有满足条件的 中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.将函数 的图象向上平移 个单位,得到的函数的边界值 满足是 时,则 的取值范围是.
15. 对某一个函数给出如下定义:若存在实数 ,对于任意的函数值 ,都满足 ,则称这个函数是有界函数 , 在所有满足条件的 中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.将函数 的图象向上平移 个单位,得到的函数的边界值 满足是 时,则 的取值范围是.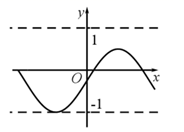
三、解答题
-
16. 计算17. 如图,已知在平面直角坐标系 中,正比例函数 的图象与反比例函数 的图象有一个交点 .
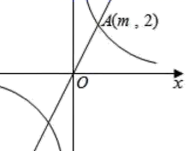 (1)、 求的值;(2)、试判断点 是否在反比例函数图象上,并说明理由.18. 在 的正方形网格中,若每一个小正方形的边长均为1,请仅用无刻度直尺按要求画图.(1)、在图1中,以 为边画一个格点正方形;
(1)、 求的值;(2)、试判断点 是否在反比例函数图象上,并说明理由.18. 在 的正方形网格中,若每一个小正方形的边长均为1,请仅用无刻度直尺按要求画图.(1)、在图1中,以 为边画一个格点正方形;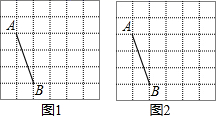 (2)、在图2中,以 为边画一个面积为6的格点四边形.
(2)、在图2中,以 为边画一个面积为6的格点四边形.(温馨提示:请画在答题卷相对应的图上)
19. “芡实糕”是一种南浔的传统特色糕点,某糕点店为了了解该地居民对去年销量较好的芝麻味(A)、紫薯味(B)、红糖味(C)、桂花味(D)四种不同口味的喜爱情况,对该地居民进行了抽样调查,并将调查情况绘制成如下两幅不完整的统计图.请根据以上信息回答:
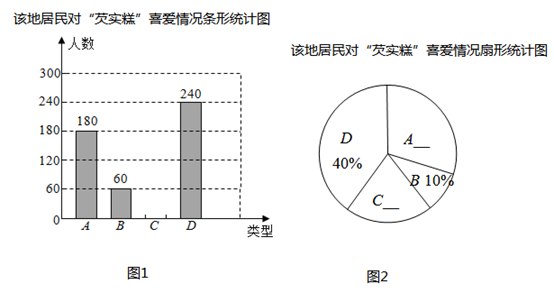 (1)、本次参加抽样调查的居民人数是多少人;(2)、请直接将两幅统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(3)、若该地居民有36000人,请估计爱吃D口味“芡实糕”有多少人?20. 如图,已知 的直径为 ,点 在圆周上(异于 , ), .
(1)、本次参加抽样调查的居民人数是多少人;(2)、请直接将两幅统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(3)、若该地居民有36000人,请估计爱吃D口味“芡实糕”有多少人?20. 如图,已知 的直径为 ,点 在圆周上(异于 , ), .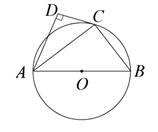 (1)、若 , ,求 的长;(2)、若 是 的平分线,求证:直线 是 的切线.21. 南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“ ”字形的墙面(粗线 表示墙面,已知 , 米, 米)和总长为11米的篱笆围建一个“日”字形的小型农场 (细线表示篱笆,小型农场中间 也是用篱笆隔开),点 可能在线段 上(如图1),也可能在线段 的延长线上(如图2),点 在线段 的延长线上.
(1)、若 , ,求 的长;(2)、若 是 的平分线,求证:直线 是 的切线.21. 南浔区某校增设拓展课程之“开心农场”,如图,准备利用现成的一堵“ ”字形的墙面(粗线 表示墙面,已知 , 米, 米)和总长为11米的篱笆围建一个“日”字形的小型农场 (细线表示篱笆,小型农场中间 也是用篱笆隔开),点 可能在线段 上(如图1),也可能在线段 的延长线上(如图2),点 在线段 的延长线上.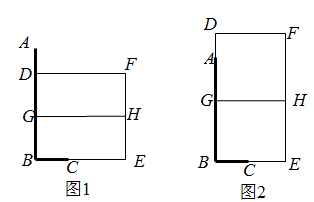 (1)、当点 在线段 上时,
(1)、当点 在线段 上时,①设 的长为 米,则 ▲ 米(用含 的代数式表示);
②若要求所围成的小型农场 的面积为9平方米,求 的长;
(2)、 的长为多少米时,小型农场 的面积最大?最大面积为多少平方米?22.(1)、特例感知
如图,已知在 中, , ,取 边上中点 ,连结 ,点 为 边上一点,连结 ,作 交 于点 ,求证 ;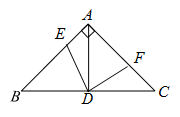 (2)、探索发现
(2)、探索发现
如图,已知在 中, , ,取 边上中点 ,连结 ,点 为 延长线上一点, ,连结 ,作 交 延长线于点 ,求 的长; (3)、类比迁移
(3)、类比迁移
如图,已知在 中, , ,取 边上中点 ,连结 ,点 为射线 上一点(不与点 、点 重合),连结 ,将射线 绕点 顺时针旋转30°交射线 于点 ,当 时,求 的长.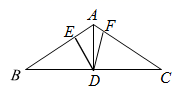 23. 如图1,已知在平面直角坐标系 中,矩形 的顶点 的坐标是 ,动点 从点 出发,沿线段 向终点 运动,同时动点 从点 出发,沿线段 向终点 运动.点 , 的运动速度均为1个单位/秒,运动时间为 秒.过点 作 交 于点 .
23. 如图1,已知在平面直角坐标系 中,矩形 的顶点 的坐标是 ,动点 从点 出发,沿线段 向终点 运动,同时动点 从点 出发,沿线段 向终点 运动.点 , 的运动速度均为1个单位/秒,运动时间为 秒.过点 作 交 于点 .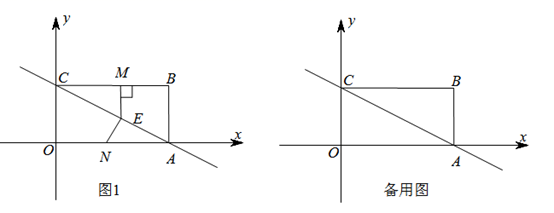 (1)、求直线 的解析式;(2)、在点 , 的运动过程中,当 为直角三角形时,请求出 的值;(3)、在动点 运动的过程中,在矩形 内(包括边界)是否存在一点 使以 , , , 为顶点的四边形是菱形,若存在,请求出 的坐标,若不存在,请说明理由.
(1)、求直线 的解析式;(2)、在点 , 的运动过程中,当 为直角三角形时,请求出 的值;(3)、在动点 运动的过程中,在矩形 内(包括边界)是否存在一点 使以 , , , 为顶点的四边形是菱形,若存在,请求出 的坐标,若不存在,请说明理由.