四川省绵阳市梓潼县2021年九年级数学中考一诊试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
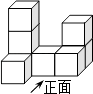
1. 下列各数中,是无理数的一项是( )A、0 B、﹣1 C、0.101001 D、2. 据省统计局发布的数据显示,截止2018年底,我省合肥市常住人口已突破800万.数据800万用科学记数法表示为( )A、8×106 B、80×104 C、0.8×107 D、8X1073. 如图是由八个相同小正方体组合而成的几何体,则其左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图, , ,∠CAD=60°, 的度数等于( )
4. 如图, , ,∠CAD=60°, 的度数等于( )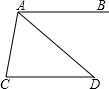 A、60° B、50° C、45° D、40°5. 请你阅读下面的诗句:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”若诗句中谈到的鸦为x只,树为y棵,则可列出方程组为( )A、 B、 C、 D、6. 已知甲、乙、丙、丁四位射击运动员在一次比赛中的平均成绩是90环(总环为100环),而乙、丙、丁三位射击运动员的平均成绩是92环,则下列说法不正确的是( )A、甲的成绩为84环 B、四位射击运动员的成绩可能都不相同 C、四位射击运动员的成绩一定有中位数 D、甲的成绩比其他三位运动员的成绩都要差7. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )
A、60° B、50° C、45° D、40°5. 请你阅读下面的诗句:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”若诗句中谈到的鸦为x只,树为y棵,则可列出方程组为( )A、 B、 C、 D、6. 已知甲、乙、丙、丁四位射击运动员在一次比赛中的平均成绩是90环(总环为100环),而乙、丙、丁三位射击运动员的平均成绩是92环,则下列说法不正确的是( )A、甲的成绩为84环 B、四位射击运动员的成绩可能都不相同 C、四位射击运动员的成绩一定有中位数 D、甲的成绩比其他三位运动员的成绩都要差7. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为( )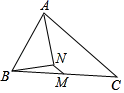 A、12 B、11 C、10 D、98. 在数-1,1,2中任取两个数作为点的坐标,该点刚好在二次函数 图象上的概率是( )A、 B、 C、 D、9. 如图,矩形ABCD的顶点A和对称中心在反比例函数 (k≠0,x>0),若矩形ABCD的面积为10,则k的值为( )
A、12 B、11 C、10 D、98. 在数-1,1,2中任取两个数作为点的坐标,该点刚好在二次函数 图象上的概率是( )A、 B、 C、 D、9. 如图,矩形ABCD的顶点A和对称中心在反比例函数 (k≠0,x>0),若矩形ABCD的面积为10,则k的值为( )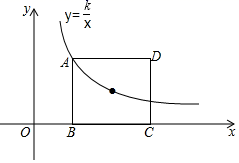 A、10 B、4 C、3 D、510. 已知 ,当 分别取得1,2,3,…,2021时,所对应 值的总和是( )A、2033 B、2032 C、2031 D、203011. 抛物线 的对称轴是直线 ,且过点 .顶点位于第二象限,其部分图象如图所示,给出以下判断:① 且 ;② ;③ ;④ ;⑤直线 与抛物线 两个交点的横坐标分别为 , ,则 .其中正确的个数有( )
A、10 B、4 C、3 D、510. 已知 ,当 分别取得1,2,3,…,2021时,所对应 值的总和是( )A、2033 B、2032 C、2031 D、203011. 抛物线 的对称轴是直线 ,且过点 .顶点位于第二象限,其部分图象如图所示,给出以下判断:① 且 ;② ;③ ;④ ;⑤直线 与抛物线 两个交点的横坐标分别为 , ,则 .其中正确的个数有( )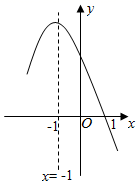 A、5个 B、4个 C、3个 D、2个12. 如图,点E、F是正方形ABCD的边BC上的两点(不与B、C两点重合),过点B作BG⊥AE于点G,连接FG、DF,若AB=2,则DF+GF的最小值为( )
A、5个 B、4个 C、3个 D、2个12. 如图,点E、F是正方形ABCD的边BC上的两点(不与B、C两点重合),过点B作BG⊥AE于点G,连接FG、DF,若AB=2,则DF+GF的最小值为( )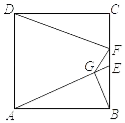 A、 ﹣1 B、 C、3 D、4
A、 ﹣1 B、 C、3 D、4二、填空题
-
13. 因式分解: .14. 若点 与点 关于 轴对称,则 值是.15. 若一个多边形的内角和是其外角的和1.5倍,则这个多边形的边数是.16. 若 , ,则 .17. 新定义:有一组对角互余的凸四边形称为对余四边形.如图,已知在对余四边形 中, , , , ,那么边 的长为 .
 18. 如图,在矩形ABCD中,AB=4 ,AD=4,点E为线段CD的中点,动点F从点C出发,沿C→B→A的方向在CB和BA上运动,将矩形沿EF折叠,点C的对应点为C',当点C'恰好落在矩形的对角线上时(不与矩形顶点重合),点F运动的距离为.
18. 如图,在矩形ABCD中,AB=4 ,AD=4,点E为线段CD的中点,动点F从点C出发,沿C→B→A的方向在CB和BA上运动,将矩形沿EF折叠,点C的对应点为C',当点C'恰好落在矩形的对角线上时(不与矩形顶点重合),点F运动的距离为.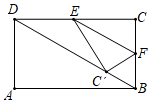
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值: ,其中 .20. 如图,在四边形ABCD中,AD=BC,∠A=∠B,E为AB的中点,连结CE,DE.
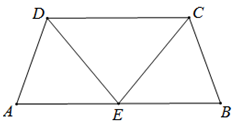 (1)、求证:△ADE≌△BCE.(2)、若∠A=70°,∠BCE=60°,求∠CDE的度数.21. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取
(1)、求证:△ADE≌△BCE.(2)、若∠A=70°,∠BCE=60°,求∠CDE的度数.21. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图: 运动项目
频数(人数)
羽毛球
30
篮球
 a
a乒乓球
36
排球
b
足球
12

请根据以上图表信息解答下列问题:
(1)、频数分布表中的a= , b=;(2)、在扇形统计图中,“排球”所在的扇形的圆心角为度;(3)、全校有多少名学生选择参加乒乓球运动?22. 如图,正比例函数y=kx(k≠0)的图象与反比例函数y=﹣ 的图象交于点A(n,2)和点B.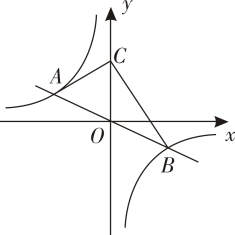 (1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.23. 如图,在 中,半径 直径 与 相切于点 连接 交 于点 交 于点 ,连接 并延长交 于点 ,连接 .
(1)、n= , k=;(2)、点C在y轴正半轴上.∠ACB=90°,求点C的坐标;(3)、点P(m,0)在x轴上,∠APB为锐角,直接写出m的取值范围.23. 如图,在 中,半径 直径 与 相切于点 连接 交 于点 交 于点 ,连接 并延长交 于点 ,连接 .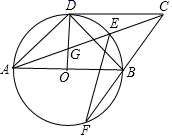 (1)、求证: ;(2)、若
(1)、求证: ;(2)、若①求证:四边形 是平行四边形;
②连接 ,当 的半径为 时,求 的长.
24. 如图,直角坐标系中,抛物线y=a(x﹣4)2﹣16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y= x+b分别交x,y轴于点A,B.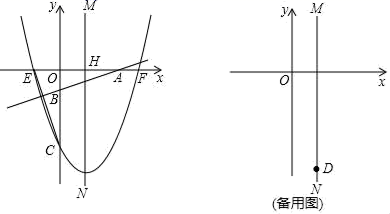 (1)、写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).(2)、若AF=AH=OH,求证:∠CEO=∠ABO.(3)、当b>﹣4时,以AB为边作正方形,使正方形的另外两个顶点一个落在抛物线上,一个落在抛物线的对称轴上,求所有满足条件的a及相应b的值.(直接写出答案即可)25. 已知四边形 是菱形, 、 交于点 ,点 在 的延长线上,连接 交 于 ,以 为直径作 ,交直线 于 、 两点,交 于 点.
(1)、写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).(2)、若AF=AH=OH,求证:∠CEO=∠ABO.(3)、当b>﹣4时,以AB为边作正方形,使正方形的另外两个顶点一个落在抛物线上,一个落在抛物线的对称轴上,求所有满足条件的a及相应b的值.(直接写出答案即可)25. 已知四边形 是菱形, 、 交于点 ,点 在 的延长线上,连接 交 于 ,以 为直径作 ,交直线 于 、 两点,交 于 点.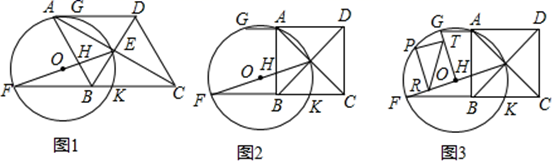 (1)、如图1,连接 ,求证:四边形 是平行四边形;(2)、如图2,当 时,求 的值;(3)、如图3,在(2)的条件下,连接 ,点 在 上,过点 作 交 于 , 交 于 点,连接 ,若 ,在点 运动过程中,探究线段 的长是否为定值,如果是定值,求出这个定值;如果不是定值,说明理由.
(1)、如图1,连接 ,求证:四边形 是平行四边形;(2)、如图2,当 时,求 的值;(3)、如图3,在(2)的条件下,连接 ,点 在 上,过点 作 交 于 , 交 于 点,连接 ,若 ,在点 运动过程中,探究线段 的长是否为定值,如果是定值,求出这个定值;如果不是定值,说明理由.