湖北省武汉市江岸区初中联合体一片2021届九年级下学期数学3月联考试卷
试卷更新日期:2021-06-28 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 若二次根式 有意义,则 为( )A、 B、 C、 D、3. 从1,3,5,7中任取两个数,则下列事件中是随机事件的是( )A、两个数的和为奇数 B、两个数的和为偶数 C、两个数的积为偶数 D、两个数的积为3的倍数4. 下列四张扑克牌中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图所示的几何体的左视图是( )
5. 如图所示的几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或7. 某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )A、 B、 C、 D、8. 八年级某生物课外兴趣小组观察一植物生长,得到植物高度 与观察时间t(天)的关系如图所示,则下列说法正确的是( ).
6. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或7. 某校开展“文明小卫士”活动,从学生会“督查部”的3名学生(2男1女)中随机选两名进行督导,恰好选中两名男学生的概率是( )A、 B、 C、 D、8. 八年级某生物课外兴趣小组观察一植物生长,得到植物高度 与观察时间t(天)的关系如图所示,则下列说法正确的是( ). A、该植物从观察时起60天以后停止长高 B、该植物最高长到16cm C、该植物从观察时起50天内平均每天长高1cm D、该植物最高长到18cm9. 如图,在 中将 沿弦 翻折过圆心O交弦 于点F, , ,则 的长为( )
A、该植物从观察时起60天以后停止长高 B、该植物最高长到16cm C、该植物从观察时起50天内平均每天长高1cm D、该植物最高长到18cm9. 如图,在 中将 沿弦 翻折过圆心O交弦 于点F, , ,则 的长为( ) A、4 B、 C、 D、610. 下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的“凸”形纸片,图2是一张由6个小正方形组成的 方格纸片.把“凸”形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的2种不同放置方法.图4是一张由36个小正方形组成的 方格纸片,将“凸”形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有n种不同放置方法,则n的值是( ).
A、4 B、 C、 D、610. 下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的“凸”形纸片,图2是一张由6个小正方形组成的 方格纸片.把“凸”形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的2种不同放置方法.图4是一张由36个小正方形组成的 方格纸片,将“凸”形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有n种不同放置方法,则n的值是( ). A、160 B、128 C、80 D、48
A、160 B、128 C、80 D、48二、填空题
-
11. 计算 的结果是.12. 在防治新型冠状病毒知识问答中10名参赛选手得分情况如下:
人数
1
3
4
2
分数
80
85
90
95
那么这10名选手所得分数的中位数.
13. .14. 如图,将 绕A点逆时针旋转60°得到 ,若 ° ,则 . 15. 二次函数 ,x与y的部分对应值如下表:当 时,下列结论中一定正确的是.(填序号即可)
15. 二次函数 ,x与y的部分对应值如下表:当 时,下列结论中一定正确的是.(填序号即可)x
-1
0
3
y
n
1
1
① ;② ;③关于x的一元二次方程 的一根在3和4之间;④当 时,y的值随x值的增大而减小.
16. 如图,已知 , 于点E, , , ,则 .
三、解答题
-
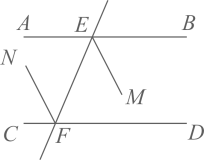
17. 计算: .18. 如图,直线 分别与直线 , 交于点E,F. 平分 , 平分 ,且 ∥ .求证: ∥ .
 19. 某校积极开展体育活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
19. 某校积极开展体育活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出) (1)、求本次被调查的学生人数,并补全条形统计图;(2)、参加篮球人数对应的圆心角为;(3)、该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?20. 如图, 的三个顶点在格点上,用无刻度的直尺在网格上画图.
(1)、求本次被调查的学生人数,并补全条形统计图;(2)、参加篮球人数对应的圆心角为;(3)、该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?20. 如图, 的三个顶点在格点上,用无刻度的直尺在网格上画图.
⑴将边 绕点C逆时针旋转90°得到线段 ;
⑵在 上找一点M,使得 ;
⑶在 上找一点F,使 .
21. 如图, 、 为 的切线,A、B为切点,点C为半圆弧的中点,连 交 于E点. (1)、求证: ;(2)、若 ,求 的值.22. 某网店经营一种热销小商品,每件成本10元,经过调研发现,这种小商品20天内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为 (其中 ,t为整数),且其日销售量y(件)与时间t(天)的关系如下表.
(1)、求证: ;(2)、若 ,求 的值.22. 某网店经营一种热销小商品,每件成本10元,经过调研发现,这种小商品20天内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为 (其中 ,t为整数),且其日销售量y(件)与时间t(天)的关系如下表.时间(天)
1
5
9
13
17
21
日销售量y(件)
98
90
82
74
66
58
(1)、已知y与t之间的变化规律符合一次函数关系,请直接写出y(件)与时间t(天)函数关系式;(2)、在20天的销售中,第几天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的20天中,该网店每销售一件商品就捐赠a元(a为整数)利润给“精准扶贫”的对象,通过销售记录发现,这20天中,每天扣除捐赠后的的日销售利润随时间t(天)的增大而增大,求a的最小值.


