四川省泸州市合江县第六片区2020-2021学年七年级上学期数学第二次月考试卷

试卷更新日期：2021-06-28 类型：月考试卷

进入出卷网下载

一、单选题

1. 低于正常水位0.16米记为﹣0.16，高于正常水位0.02米记作（）

A、+0.02 B、﹣0.02 C、+0.18 D、﹣0.14

查看试题解析
2. 中国的“天眼”绝对是我们中国人的骄傲，它可以一眼看穿 $130$ 亿光年以外，换句话来说就是可以接收到 $130$ 亿光年之外的电磁信号，几乎已经可以达到我们人类现在所了解到的宇宙的极限边缘.数据 $130$ 亿正确的表示是（）

A、 $1.3 \times 10^{10}$ B、 $1.30 \times 10^{10}$ C、 $0.13 \times 10^{10}$ D、 $130 \times 10^{9}$

查看试题解析
3. 下列平面图形中，经过折叠不能围成正方体的是（）

A、 B、 C、 D、

查看试题解析
4. 下列现象中，可用基本事实“两点之间，线段最短”来解释的现象是（）

A、用两个钉子就可以把木条固定在墙上 B、利用圆规可以比较两条线段的大小关系 C、把弯曲的公路改直，就能缩短路程 D、植树时，只要定出两棵树的位置，就能确定同一行树所在的直线

查看试题解析
5. 下列代数式中整式有（）
$\frac{1}{x}$ ， $2 x + y$ ， $\frac{1}{3} a b$ ， $\frac{x - y}{π}$ ， $\frac{5 y}{4 x}$ ， $0.5$ ， $a$

A、 $4$ 个 B、 $5$ 个 C、 $6$ 个 D、 $7$ 个

查看试题解析
6. 若 $3 a^{m + 2} b$ 与 $\frac{1}{2} a b^{n - 1}$ 是同类项，则 $m + n =$ （）

A、-2 B、1 C、2 D、-1

查看试题解析
7. 下列运用等式的性质进行的变形，不正确的是（）

A、若 $x = t$ ，则 $x - 5 = t - 5$ B、若 $a = b$ ，则 $a c = b c$ C、若 $x = y$ ，则 $x + a = y + a$ D、若 $x = y$ ，则 $\frac{x}{a} = \frac{y}{a}$

查看试题解析
8. 已知方程 $(a + 3) x^{| a | - 2} + 1 = 0$ 是关于x的一元一次方程，则关于y的方程 $a y + 6 = 0$ 的解是（）

A、y=2 B、y=－2 C、y=2或y=－2 D、y=1

查看试题解析
9. 已知 $a$ ， $b$ 在数轴上的位置如图所示，则 $| a | + | a + b 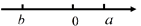| - | a - b |$ 的值为（）

A、a+2b B、 $- a - 2 b$ C、 $- a$ D、 $a$

查看试题解析
10. 已知a+4b＝﹣ $\frac{1}{5}$ ，那么代数式9（a+2b）﹣2（2a﹣b）的值是（）

A、﹣ $\frac{1}{5}$ B、﹣1 C、 $\frac{1}{5}$ D、1

查看试题解析
11. 为了迎接暑假的购物高峰，北碚万达广场耐克专卖店购进甲、乙两种服装，现此商店同时卖出甲、乙两种服装各一件，每件售价都为240元，其中一件赚了20%，另一件亏了20%，那么这个商店卖出这两件服装总体的盈亏情况是（）

A、赚了12元 B、亏了12元 C、赚了20元 D、亏了20元

查看试题解析
12. 我们知道 $1 + 2 + 3 + ... + 100 = 5050$ ，于是 $m + 2 m + 3 m + \dots + 100 m = 5050 m$ ，那么合并同类项 $m + 2 m + 3 m + ... + 51 m$ 的结果是（）

A、 $1570 m$ B、 $1576 m$ C、 $1326 m$ D、 $1323 m$

查看试题解析

二、填空题

13. 单项式 $- \frac{1}{3} π a^{3} b c^{2}$ 的系数是、次数是

查看试题解析
14. 若 $| a | = 2$ ， $| b | = 5$ ，且 $a > b$ ，则 $a + b =$

查看试题解析
15. 若 $x$ ， $y$ 互为相反数， $a$ 、 $b$ 互为例数，则代数式 $2020 x + 2020 y - \frac{a b}{2}$ 的值是．

查看试题解析
16. 一组按规律排列的式子： $\frac{2}{a} ， - \frac{5}{a^{2}} ， \frac{10}{a^{3}} ， - \frac{17}{a^{4}} ， \frac{26}{a^{5}}$ ，···，第 $n$ 个式子是.（用含 $n$ 的式子表示， $n$ 为正整数）.

查看试题解析

三、解答题

17. 计算： ${(- 5)}^{3} \times (- \frac{3}{5}) + 32 \div (- 2^{2}) \times (- 1 \frac{1}{4})$

查看试题解析
18. 解方程： $\frac{3 x + 2}{2} - 1 = \frac{2 x + 1}{4} - \frac{2 x + 1}{5}$

查看试题解析
19. 如图，按下列要求完成作图.

（ 1 ）画直线 $A B$ 及线段 $A C$ ；

（ 2 ）连接 $C D$ 并延长 $C D$ 到 $E$ 点，使 $C E = 2 C D$

查看试题解析
20. 用白铁皮做罐头盒，每张铁皮可制盒身25个或制盒底40个，一个盒身与两个盒底配成一套，现有36张白铁皮，用多少张制盒身，多少张制盒底，可使盒身与盒底正好配套？

查看试题解析
21. 定义新运算：对于任意有理数 $a$ ， $b$ ，都有 $a * b = b^{2} + a$ ，例如： $7 * 4 = 4^{2} + 7 = 23$

(1)、求 $5 * 3$ 的值；

(2)、求 $(- 2) * [(- 5) * 2]$ 的值.

查看试题解析

22. 某次篮球联赛中，两队的积分如下表所示：

队名	比赛场次	胜场场次	负场场次	积分
前进	14	10	4	24
钢铁	14	0	14	14

请回答下列问题：

(1)、负一场积分；

(2)、求胜一场积多少分？

(3)、某队的胜场总积分比负场总积分的3倍多3分，求该队胜了多少场？

查看试题解析

23. 若关于x、y的代数式 $({ax}^{2} + 2 x + 3 y - 5) - 2 (x^{2} - bx - 2 y + 4)$ 的值与字母x的取值无关

(1)、求a，b的值；

(2)、求 $2 (a^{2} b - {ab}^{2}) - 3 (2 {ab}^{2} + a^{2} b - 2)$ 的值.

查看试题解析

24. 某省公布的居民用电阶梯电价听证方案如下：

项目	第一档	第二档	第三档
用电量（度）	210度以下	210至350	350度以上
价格（元）	0.52	比第一档提价0.05元	比第一档提价0.3元

例：若某户月用电量400度，则需交电费为210×0.52＋（350－210）×（0.52＋0.05）＋（400－350）×（0.52＋0.30）＝230（元）.

(1)、如果按此方案计算，小华家5月份的电费为138.84元，请你求出小华家5月份的用电量；

(2)、以此方案请你回答：若小华家某月的电费为a元，则小华家该月用电量属于第几档？

查看试题解析

25. 如图 $1$ ， $C$ 是线段 $A B$ 上的点， $M$ ， $N$ 分别是 $A C$ ， $B C$ 的中点.

(1)、若 $A C = 6 c m ， B C = 4 c m$ ，求线段 $M N$ 的长度；

(2)、若 $A C = 6 c m$ ， $M N = 5 c m$ ，求线段 $M B$ 的长度；

(3)、说明 $M N$ 与 $A B$ 之间的数量关系；

(4)、如图 $2$ ，若 $C$ 是线段 $A B$ 延长线上的点， $M$ ， $N$ 分别是 $A C$ ， $B C$ 的中点，直接写出 $M N$ 与 $A B$ 之间的数量关系.

查看试题解析