陕西省西安市2020-2021学年七年级上学期数学月考试卷
试卷更新日期:2021-06-28 类型:月考试卷
一、单选题
-
1. -2的倒数是( )A、-2 B、 C、 D、22. 下列几何体中截面不可能是长方形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 与 是同类项的是( )A、 B、 C、 D、4. 若 ,则 的值为( )A、1 B、 C、0 D、20205. 陕西省位于中国中部黄河中游地区,南部兼跨长江支流汉江流域和嘉陵江上游的秦巴山地区,总面积约20.6万平方千米,其中“20.6万”用科学记数法表示为( )A、 B、 C、 D、6. 买一个排球需要m元,买一个足球需要n元,则买4个足球和7个排球共需要( )A、 元 B、 元 C、 元 D、 元7. 如图是一个正方体展开图,把展开图折叠成正方体后,与“忆”字相对面上的字是( )
3. 与 是同类项的是( )A、 B、 C、 D、4. 若 ,则 的值为( )A、1 B、 C、0 D、20205. 陕西省位于中国中部黄河中游地区,南部兼跨长江支流汉江流域和嘉陵江上游的秦巴山地区,总面积约20.6万平方千米,其中“20.6万”用科学记数法表示为( )A、 B、 C、 D、6. 买一个排球需要m元,买一个足球需要n元,则买4个足球和7个排球共需要( )A、 元 B、 元 C、 元 D、 元7. 如图是一个正方体展开图,把展开图折叠成正方体后,与“忆”字相对面上的字是( ) A、时 B、月 C、长 D、安8. 下列运算中正确的是( )A、 B、 C、 D、9. 下列判断正确的是( )A、 的次数是2 B、0不是单项式 C、 的系数是 D、 是四次三项式10. 如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着 , , ,0,且任意相邻四个台阶上的数的和都相等,则前37个台阶上的数的和是( )
A、时 B、月 C、长 D、安8. 下列运算中正确的是( )A、 B、 C、 D、9. 下列判断正确的是( )A、 的次数是2 B、0不是单项式 C、 的系数是 D、 是四次三项式10. 如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着 , , ,0,且任意相邻四个台阶上的数的和都相等,则前37个台阶上的数的和是( )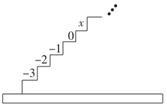 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 比较大小: ;
12. 去括号应得.13. 如图,根据图中的运算程序进行计算,当输入 时,输出的结果为. 14. 如图,在棱长分别为 、 、 的长方体中截掉一个棱长为 的正方体,则剩余几何体的表面积为.
14. 如图,在棱长分别为 、 、 的长方体中截掉一个棱长为 的正方体,则剩余几何体的表面积为.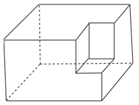
三、解答题
-
15. 计算: .16. 将下列各数在如图的数轴上表示出来,然后用“ ”连接起来.
、 、 、 .
 17. 分析图中几何体,请在下面的网格图中画出该几何体分别从正面、左面及上面所看到的形状图.
17. 分析图中几何体,请在下面的网格图中画出该几何体分别从正面、左面及上面所看到的形状图. 18. 某村种植了小麦、水稻、玉米三种农作物,小麦种植面积是 亩,水稻种植面积是小麦种植面积的4倍,玉米种植面积比小麦种植面积的2倍少3亩问:(1)、水稻种植面积:(含 的式子表示)(2)、水稻种植面积和玉米种植面积哪一个大?为什么?19. 如图所示的是一个几何体的表面展开图.
18. 某村种植了小麦、水稻、玉米三种农作物,小麦种植面积是 亩,水稻种植面积是小麦种植面积的4倍,玉米种植面积比小麦种植面积的2倍少3亩问:(1)、水稻种植面积:(含 的式子表示)(2)、水稻种植面积和玉米种植面积哪一个大?为什么?19. 如图所示的是一个几何体的表面展开图. (1)、该几何体的名称是.(2)、根据图中所给信息,求该几何体的体积(结果保留 ).20. 先化简,再求值: ,其中 .21.(1)、所有负数组成负数集合,所有整数组成整数集合,请你把下列各数填入它所属的集合的圈内:3.6, ,0, , ,2.
(1)、该几何体的名称是.(2)、根据图中所给信息,求该几何体的体积(结果保留 ).20. 先化简,再求值: ,其中 .21.(1)、所有负数组成负数集合,所有整数组成整数集合,请你把下列各数填入它所属的集合的圈内:3.6, ,0, , ,2.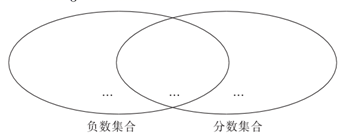 (2)、这两个圈的重叠部分表示什么数的集合?(3)、列式并计算:在(1)的数据中,求最大的数与最小的数的和.22. 我们知道 和 的结果互为倒数,这个规律可以运用到简便计算中.
(2)、这两个圈的重叠部分表示什么数的集合?(3)、列式并计算:在(1)的数据中,求最大的数与最小的数的和.22. 我们知道 和 的结果互为倒数,这个规律可以运用到简便计算中.例如:计算 时,我们可以先计算 ,
所以 .仿照上面的方法计算 .
23. 已知代数式 ,晓晴错将求代数式“ ”看成求代数式“ ”,算得结果 .(1)、求代数式A.(2)、求代数式C.