江苏省徐州市睢宁县2020-2021学年七年级上学期数学12月月考试卷
试卷更新日期:2021-06-28 类型:月考试卷
一、单选题
-
1. 下列算式中,运算结果为负数的是( )A、 B、 C、 D、2. 下列运算中,正确的是( )A、 B、 C、 D、3. 运用等式性质进行的变形,正确的是( )A、如果a=b,那么a+c=b-c; B、如果 , 那么a=b; C、如果a=b,那么; D、如果=3a,那么a=34. 已知x=2是方程2x﹣5=x+m的解,则m的值是( )A、1 B、﹣1 C、3 D、﹣35. 我校初一学生参加2020年元旦联欢晚会,设学校报告厅有座位 排,若每排坐 人,则有 人无座位:每排坐 人,则空 个座位,则下列方程正确的是( )A、 B、 C、 D、6. 下列图形中,不是立方体表面展开图的是( )A、
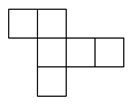 B、
B、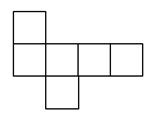 C、
C、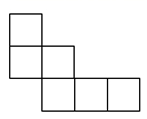 D、
D、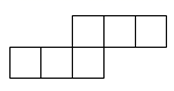 7. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥8. 一个几何体的三视图如图所示,则这个几何体是( )
7. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥8. 一个几何体的三视图如图所示,则这个几何体是( ) A、四棱锥 B、四棱柱 C、三棱锥 D、三棱柱
A、四棱锥 B、四棱柱 C、三棱锥 D、三棱柱二、填空题
-
9. ﹣3的倒数为 .10. 已知地球的表面积约为510000000km2.数510000000用科学记数法可以表示为.11. 若 是关于 的一元一次方程,则 的值为.12. 当x=时,代数式2x+1与5x﹣6的值互为相反数.13. 某种商品的标价为 元,若以九折降价出售,仍可获利 ,设该商品的进货价为 元,可列方程为.14. 用边长为 的正方形纸板,制成一个七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为.
 15. 如图,若要使图中的平面展开图折叠成正方形,相对面上两个数相等,则 .
15. 如图,若要使图中的平面展开图折叠成正方形,相对面上两个数相等,则 . 16.
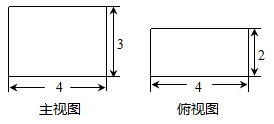
16.长方体的主视图与俯视图如图所示,则这个长方体的体积是.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、3x+4-5(x+1)=-1;(2)、 - =1.19. 规定一种新运算法则: ,例如(1)、求 的值:(2)、若 ,求(-2)※x的值20. 由大小相同,棱长为 的小立方体块搭成的几何体如下图所示.(1)、请在下图的方格纸中分别画出该几何体的主视图和左视图:

 (2)、该几何体的表面积为 (包括底面积);(3)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以添加个小正方体.21. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(2)、该几何体的表面积为 (包括底面积);(3)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以添加个小正方体.21. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: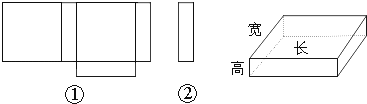 (1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.22. 星星果汁店中的 种果汁比 种果汁每杯贵2元,小明和同学买了2杯 种果汁和3杯 种果汁,一共花了54元. 种果汁和 种果汁每杯分别是多少元?若设 种果汁每杯 元.(1)、用含 的代数式填空;
(1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.22. 星星果汁店中的 种果汁比 种果汁每杯贵2元,小明和同学买了2杯 种果汁和3杯 种果汁,一共花了54元. 种果汁和 种果汁每杯分别是多少元?若设 种果汁每杯 元.(1)、用含 的代数式填空;品名
单价(元/杯)
数量(杯)
金额(元)
种果汁
2
种果汁
3
(2)、列一元一次方程解决问题.23. 列方程解应用题:甲、乙两站相距 一列慢车从甲站出发开往乙站,速度为 一列快车从乙站出发开往甲站,速度为 .
(1)、两车同时出发,出发后多少时间两车相遇?(2)、慢车先出发 ,快车开出后多少时间两车相距 ?24. 某商场开展春节促销活动出售A、B两种商品,活动方案如下两种:方案一
A
B
每件标价
90元
100元
每件商品返利
按标价的30%
按标价的15%
例如买一件A商品,只需付款90(1﹣30%)元
方案二
所购商品一律按标价的20%返利
(1)、某单位购买A商品30件,B商品20件,选用何种方案划算?能便宜多少钱?(2)、某单位购买A商品x件(x为正整数),购买B商品的件数是A商品件数的2倍少1件,若两方案的实际付款一样,求x的值.