浙江省2021年八年级下学期数学期末模拟(嘉兴、金华、湖州、丽水、衢州、舟山适用）

试卷更新日期：2021-06-27 类型：期末考试

进入出卷网下载

一、选择题

1. 化简 $\sqrt{{(- 3)}^{2}}$ 的值是（　　）

A、﹣3 B、3 C、±3 D、9

查看试题解析
2. 如图，下列四组图形中的两个三角形是中心对称关系的是（）

A、 B、 C、 D、

查看试题解析
3. 在反比例函数y＝ $\frac{6}{x}$ 的图象上横、纵点坐标都是整数的点有（）

A、2个 B、4个 C、6个 D、8个

查看试题解析
4. 用反证法证明“在同一平面内，若 $a ⊥ c$ ， $b ⊥ c$ ，则 $a // b$ ”时，应假设（）

A、 $a // c$ B、 $b // c$ C、 $a // c$ ， $b // c$ D、 $a$ 与 $b$ 相交

查看试题解析
5. 去年某果园随机从甲、乙、丙、丁四个品种的苹果树上各采摘了15棵，四个品种的苹果树产量的平均数 $\bar{x}$ （单位：千克）及方差 $s^{2}$ （单位：千克²）如表所示：

甲

乙

丙

丁

$\bar{x}$

25

24

25

20

$s^{2}$

1.8

1.8

2

1.9

今年准备从四个品种中选出一种产量既高又稳定的苹果树进行种植，应选的品种是（）

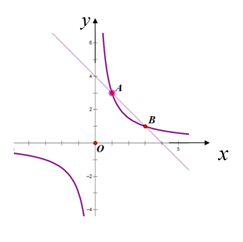
A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 下列四个命题中错误的是（）

A、对角线相等的菱形是正方形 B、有两边相等的平行四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分的四边形是平行四边形

查看试题解析
7. 用配方法解方程 $x^{2} - 6 x - 4 = 0$ ，下列配方正确的是（）

A、 ${(x - 3)}^{2} = 13$ B、 ${(x + 3)}^{2} = 13$ C、 ${(x - 6)}^{2} = 4$ D、 ${(x - 3)}^{2} = 5$

查看试题解析
8. 如图，正方形ABCD在平面直角坐标系中的点A和点B的坐标为A(1，0)、B(0，3)，点D在双曲线y= $\frac{k}{x}$ (k≠0)上.若正方形沿x轴负方向平移m个单位长度后，点C恰好落在该双曲线上，则m的值是（）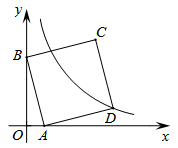

A、1 B、2 C、3 D、4

查看试题解析
9. 矩形一个角的平分线分矩形一边为2cm和3cm两部分，则这个矩形的面积为（）

A、10cm² B、15cm² C、12cm² D、10cm²或15cm²

查看试题解析
10. 已知关于 $x$ 的方程 $x^{2} - (m + 1) x + 2 m - 1 = 0$ 的两根互为倒数，则 $m$ 的值为（）

A、 $- 1$ B、 $\frac{1}{2}$ C、 $1$ D、 $- \frac{1}{2}$

查看试题解析

二、填空题

11. 当x时，式子 $\frac{1}{\sqrt{x - 4}}$ 有意义．

查看试题解析
12. 若正多边形的内角和是540°，那么这个多边形一定是正边形.

查看试题解析
13. 如图，在四边形ABCD中，点P是对角线BD的中点，点 $E ， F$ 分别是AB，CD的中点， $A D = B C$ ， $∠ P E F = 25^{\circ}$ ，则 $∠ P F E$ 的度数是.

查看试题解析
14. 如图，正方形 $A B C D$ 的边长是2，对角线AC、BD相交于点O，点E、F分别在边AD、AB上，且 $O E ⊥ O F$ ，则四边形 $A F O E$ 的面积为．

查看试题解析
15. 如图，在平面直角坐标系中，正方形 $A B C D$ 的边长为2，点 $A$ 的坐标为 $(1 ， 1)$ ．若直线 $y = x + b$ 与正方形有两个公共点，则 $b$ 的取值范围是．

查看试题解析
16. 如图，菱形ABCD的对角线AC、BD交于点O，其中AC＝8，BD＝6，以OC、OB为边作矩形OBEC，矩形OBEC的对角线OE、BC交于点F，再以CF、FE为边作第一个菱形CFEG，菱形CFEG的对角线FG、CE交于点H，如此继续，第n个菱形的周长等于.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} \times \sqrt{50} \div 2 \sqrt{6}$ ；

(2)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$ .

查看试题解析
18. 解方程：

(1)、 ${(2 x + 3)}^{2} - 81 = 0$

(2)、 $x^{2} - 4 x - 5 = 0$

查看试题解析

19. 某校八年级两个班各选派10名学生参加“垃圾分类知识竞赛，各参赛选手的成绩如下：

八（1）班：88，91，92，93，93，93，94，98，98，100；

八（2）班：89，93，93，93，95，96，96，98，98，99

通过整理，得到数据分析表如下

班级	最高分	平均分	中位数	众数	方差
八（1）班	100	$a$	93	93	12
八（2）班	99	95	$b$	$c$	8.4

(1)、求表中

a

，

b

，

c

的值；

(2)、依据数据分析表，有同学认为最高分在（1）班，（1）班的成绩比（2）班好．但也有同学认为（2）班的成绩更好．请你写出两条支持八（2）班成绩更好的理由．

查看试题解析

20. 如图，反比例函数 $y_{1} = \frac{m}{x}$ 的图像与一次函数 $y_{2} = k x + b$ 的图像交于A、B两点.已知A (2，n），B（ $- \frac{1}{2}$ ， $- 2$ ）.

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积；

(3)、请结合图像直接写出当y₁≥y₂时自变量x的取值范围.

查看试题解析
21. 如图，在四边形ABCD中，AD∥BC，CA平分∠DCB，DB平分∠ADC

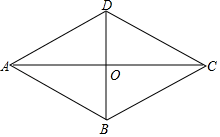(1)、求证：四边形ABCD是菱形；

(2)、若AC＝8，BD＝6，求点D到AB的距离

查看试题解析
22. 阅读材料：
用配方法可以解一元二次方程，还可以用它来解决很多问题．例如：因为3a²≥0，所以3a²+1就有最小值1，即3a²+1≥1，只有当a=0时，才能得到这个式子的最小值1．同样，因为-3a²≤0，所以-3a²+1有最大值1，即-3a²+1≤1，只有在a=0时，才能得到这个式子的最大值1．

(1)、当x=时，代数式3（x+3）²+4有最小（填写大或小）值为．

(2)、当x=时，代数式-2x²+4x+3有最大（填写大或小）值为.

(3)、矩形花园的一面靠墙，另外三面的栅栏所围成的总长度是16m，当花园与墙相邻的边长为多少时，花园的面积最大？最大面积是多少？

查看试题解析
23. 如图，反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = - x + b$ 的图象交于点A（1，3）和点B.

(1)、求 $k$ 的值和点B的坐标.

(2)、结合图象，直接写出当不等式 $\frac{k}{x} < - x + b$ 成立时 $x$ 的取值范围.

(3)、若点C是反比例函数 $y = \frac{k}{x}$ 第三象限图象上的一个动点，当 $CA = CB$ 时，求点C的坐标.

查看试题解析
24. 如图，在菱形ABCD中，AE⊥BC于点E．

(1)、若∠BAE=30°，AE=3，求菱形ABCD的周长．

(2)、作AF⊥CD于点F，连结EF，BD，求证：EF∥BD．

(3)、设AE与对角线BD相交于点G，若CE=4，BE=8，四边形CDGE和△AGD的面积分别是S₁和S₂ ，求S₁-S₂是的值．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	25	24	25	20
$s^{2}$	1.8	1.8	2	1.9