浙江省2021年八年级下学期数学期末模拟(杭州适用)
试卷更新日期:2021-06-27 类型:期末考试
一、仔细选一选(本题有10个小题,每小题3分,共30分。每小题给出的四个选项中,只有一个是正确的,请选出正确的选项.注意可以用多种不同的方法来选取正确答案。)
-
1. 若点A(x,3)与点B(2,y)关于原点对称,则( )A、x=﹣2,y=﹣3 B、x=2,y=3 C、x=﹣2,y=3 D、x=2,y=﹣32. 下列运算中,正确的是( )A、 B、 C、 D、3. 已知一个正多边形的内角为a度,则下列不可能是a的值的是( )A、90 B、100 C、120 D、176.44. 用配方法解一元二次方程 时,方程变形正确的是( )A、 B、 C、 D、5. 测试五位学生的“ 米”跑成绩,得到五个各不相同的数据,在统计时,出现了一处错误:将跑的最快一名学生成绩写得更快了,则计算结果不受影响的是( )A、总成绩 B、方差 C、中位数 D、平均数6. 用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )A、没有一个角不小于60° B、没有一个角不大于60° C、所有内角不大于60° D、所有内角不小于60°7. 如图,两双曲线y= 与y=﹣ 分别位于第一、四象限,A是y轴上任意一点,B是y=﹣ 上的点,C是y= 上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y= 在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣ );③k=4;④△ABC的面积为定值7,正确的有( )
 A、①② B、①③ C、②③ D、③④8. 菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为( )A、40 cm B、20 cm C、10 cm D、5 cm9. 已知方程x2+mx+n=0的两根为x1、x2(x1<x2),方程x2+mx+n﹣1=0的两根为x3、x4(x3<x4),则下列关系一定成立的是( )A、x1<x2<x3<x4 B、x1<x3<x4<x2 C、x3<x4<x1<x2 D、x3<x1<x2<x410. 如图,矩形纸片 , ,将其折叠使点 与点 重合,点 的对应点为点 ,折痕为 ,那么 和 的长分别为( )
A、①② B、①③ C、②③ D、③④8. 菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为( )A、40 cm B、20 cm C、10 cm D、5 cm9. 已知方程x2+mx+n=0的两根为x1、x2(x1<x2),方程x2+mx+n﹣1=0的两根为x3、x4(x3<x4),则下列关系一定成立的是( )A、x1<x2<x3<x4 B、x1<x3<x4<x2 C、x3<x4<x1<x2 D、x3<x1<x2<x410. 如图,矩形纸片 , ,将其折叠使点 与点 重合,点 的对应点为点 ,折痕为 ,那么 和 的长分别为( )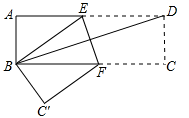 A、4和 B、4和 C、5和 D、5和
A、4和 B、4和 C、5和 D、5和二、认真填一填(本题有6个小题,每小题4分,共24分.注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.)
-
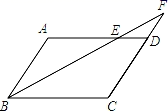
11. 要使代数式 有意义,则x的取值范围是 .12. 如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的角平分线交AD于点E,交CD的延长线于点F,则DE=cm.
 13. 关于 的一元二次方程 有一个解是 ,则 .14. 对于样本数据1,2,3,2,2,以下判断:①平均数为2;②中位数为2;③众数为2;④极差为2;⑤方差为2.正确的有(填序号).15. 如图,矩形 的边 与x轴平行,顶点A的坐标为(2,1),点B,D都在反比例函数 的图象上,则矩形ABCD的面积为.
13. 关于 的一元二次方程 有一个解是 ,则 .14. 对于样本数据1,2,3,2,2,以下判断:①平均数为2;②中位数为2;③众数为2;④极差为2;⑤方差为2.正确的有(填序号).15. 如图,矩形 的边 与x轴平行,顶点A的坐标为(2,1),点B,D都在反比例函数 的图象上,则矩形ABCD的面积为.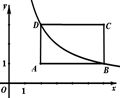 16. 如果一个正比例函数的图象与反比例函数y= 交于A(x1 , y1),B(x2 , y2),那么(x1﹣x2)(y1﹣y2)=.
16. 如果一个正比例函数的图象与反比例函数y= 交于A(x1 , y1),B(x2 , y2),那么(x1﹣x2)(y1﹣y2)=.三、全面答一答(本题有7个小题,共66分:解答应写出文字说明,证明过程或推演步骤如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以。)
-
17. 计算:①
②
18. 选用适当的方法解下列方程.(1)、x2-4x-3 =0;(2)、3x(x+1)=2(x+1).19. 甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题进球数/个
10
9
8
7
6
5
甲
1
1
1
4
0
3
乙
0
1
2
5
0
2
(1)、分别写出甲、乙两班选手进球数的平均数、中位数与众数;(2)、如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?20. 为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。(1)、x的值是多少?(2)、再经过几轮转发后,参与人数会超过10000人?21. 已知:在 中,AD是BC边上的中线,点E是AD的中点;过点A作 ,交BE的延长线于F,连接CF. (1)、证明:四边形ADCF是平行四边形;(2)、填空:
(1)、证明:四边形ADCF是平行四边形;(2)、填空:当 时,四边形ADCF是形;
当 时,四边形ADCF是形

