浙江省2021年八年级下学期数学期末模拟(宁波、绍兴、台州适用）
试卷更新日期：2021-06-27 类型：期末考试
一、选择题(本题有10小题，每小题4分，共40分)
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 二次根式 中字母x的取值范围是（ ）A、x≥2 B、x＞2 C、x≥ D、x＞3. 用反证法证明命题：“一个三角形中不能有两个直角”，应先设这个三角形中（ ）A、有两个角是直角 B、有另个角是直角 C、有两个角是锐角 D、三个角都是直角4. 甲、乙两人在2020年上半年每月电费支出情况的统计图如图所示，则他们在2020年上半年月电费支出的方差S2甲和S2乙的大小关系是（ ）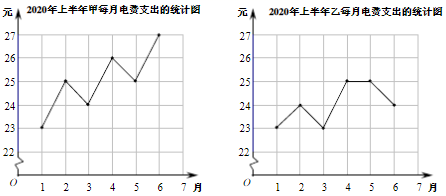
A、 ＜ B、 ＝ C、 ＞ D、无法确定5. 用配方法解一元二次方程x2+4x+1＝0，下列变形正确的是（ ）A、（x﹣2）2﹣3＝0 B、（x+4）2＝15 C、（x+2）2＝15 D、（x+2）2＝36. 已知反比例函数y= ， 下列结论中不正确的是（ ）A、图象必经过点（1，﹣5） B、y随x的增大而增大 C、图象在第二、四象限内 D、若x＞1，则﹣5＜y＜07. 若一元二次方程x（kx+1）﹣x2+3＝0无实数根，则k的最小整数值是（ ）A、2 B、1 C、0 D、﹣18.在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m3）与体积v（单位：m3）满足函数关系式ρ=（k为常数，k≠0）其图象如图所示，则k的值为( ）
A、9 B、－9 C、4 D、－49. 如图，在菱形ABCD中，E是AB边上一点，且∠A=∠EDF=60°，有下列结论：①AE=BF；
②△DEF是等边三角形；
③△BEF是等腰三角形；
④当AD=4时，△DEF的面积的最小值为 ．
其中结论正确的个数是（ ）
A、1 B、2 C、3 D、410. 如图，▱ABCD的周长为24，对角线AC，BD相交于点O，点E是CD的中点，BD=8，则△DOE的周长为（ ）
A、6 B、8 C、10 D、14二、填空题(本题有6小题，每小题5分，共30分)
-
11. 当 ，二次根式 的值是.12. 若一个正多边形的每一个外角都是30°，则这个正多边形的内角和等于度.13. 如图，在矩形ABCD中，对角线AC与BD相交于点O，∠AOB=60°，AE平分∠BAD，AE交BC于E，则∠BOE的大小为 ．
14. 某校规定：学生的数学期末总评成绩由卷面成绩、研究性学习成绩、平时成绩三部分构成，各部分所占比例如图所示，小明本学期数学学科的卷面成绩、研究性学习成绩、平时成绩得分依次为90分、80分、85分，则小明的数学期末总评成绩为分。
15. 在温度不变的条件下，一定质量的气体的压强p与它的体积V成反比例，当V=200时，P=50，则当P=25时，V= ．16. 如图，有一张矩形纸条ABCD，AB=15cm，BC=4cm，点M、N分别在边AB、CD上，CN=3cm。现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上，当点B'恰好落在边CD上时，线段BM的长为cm ；在点M从点A运动到点B的过程中，若边MB'与CD交于点E，则点E相应运动的路径长为cm。
三、共8题，共80分
-
17.(1)、计算：(2)、计算： .18. 解方程：(1)、（ +4）²=5（ +4）
(2)、2x2+4x-3=019. 某校为了解学生的课外阅读情况．随机抽查了八年级部分学生一学期阅读课外书册数的情况，并绘制出如下不完整的统计图．根据图中提供的信息，解答下列问题：
(1)、求被抽查的学生总人数，并补全条形图；(2)、写出阅读书册数的众数和中位数；(3)、若八年级共有800人，请你估计该年级阅读书册数为6册的同学约为多少人？20. 已知：如图，在菱形ABCD中， BE⊥AD于点E ， 延长AD至F ， 使DF=AE ， 连接CF ．
(1)、判断四边形EBCF的形状，并证明；(2)、若AF=9，CF=3，求CD的长．21. 2020年3月，新冠肺炎疫情在中国已经得到有效控制，但在全球却开始持续蔓延，这是对人类的考验，将对全球造成巨大影响．新冠肺炎具有人传人的特性，若一人携带病毒，未进行有效隔离，经过两轮传染后共有169人患新冠肺炎（假设每轮传染的人数相同）．求：(1)、每轮传染中平均每个人传染了几个人？(2)、如果这些病毒携带者，未进行有效隔离，按照这样的传染速度，第三轮传染后，共有多少人患病？22. 已知如图，一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点，A点坐标是（﹣2，1），B点坐标（1，n）；
(1)、求出k，b，m，n的值；(2)、求△AOB的面积；(3)、直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围．23. 如图正方形ABCD，点E、G、H分别在AB、AD、BC上，DE与HG相交于点O.
(1)、如图1，当∠GOD=90°，①求证：DE=HG
②平移图1中线段GH，使G点与D重合，H点在BC延长线上，连接EH，取EH中点P，连接PC，如图2，求证：BE= PC；
(2)、如图3，当∠GOD=45°，边长AB=4，HG= ，则DE的长为（直接写出结果）.24. 我们定义：对角线互相垂直的四边形叫做“对垂四边形”。
(1)、如图1，四边形ABCD为“对垂四边形”。求证：AB²+CD2=BC2+AD²(2)、如图2，E是四边形ABCD内一点，连结AE，BE，CE和DE，AC与BD交于点O。若∠BEC=90°，∠BAC=∠BDC，∠1+∠2=∠3。求证：四边形ABCD为“对垂四边形”。(3)、如图3，四边形ABCD为“对垂四边形”，AB=AC，∠ADC=120°，AD=3，BC= DC。求CD的长。