浙江省2021年七年级下学期数学期末模拟(温州适用）

试卷更新日期：2021-06-27 类型：期末考试

进入出卷网下载

一、选择题

1. 如图，下列说法不正确的是（）

A、∠AFE与∠EGC是同位角 B、∠AFE与∠FGC是内错角 C、∠C与∠FGC是同旁内角 D、∠A与∠FGC是同位角

查看试题解析
2. 某种新型冠状病毒的直径为0.000000053米，将0.000000053用科学记数法表示为（）

A、53×10^﹣⁸ B、5.3×10^﹣⁷ C、5.3×10^﹣⁸ D、5.3×10^﹣⁹

查看试题解析
3. 计算（-2a²）•3a³的结果，正确的是（）

A、-6a⁵ B、6a⁵ C、
-2a⁶
D、2a⁶

查看试题解析
4. 若一个二元一次方程的一个解为 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ ，则这个方程可以是（）

A、 $y - x = 1$ B、 $x - y = 1$ C、 $x + y = 1$ D、 $x + 2 y = 1$

查看试题解析
5. 为做好预防学生沉迷网络教育引导工作，某中学要求学生家长反馈学生使用网络的基本情况，小舟家长记录了小舟一周使用网络的时间，并将统计结果绘制成如图所示的折线统计图，则小舟这一周使用网络时间超过3个小时的有（　　）

A、1天 B、2天 C、3天 D、4天

查看试题解析
6. 下列计算正确的是（）

A、 $2 m (m - 1) = 2 m^{2} - 1$ B、 ${(- m^{2})}^{3} = - m^{6}$ C、 $m^{3} - m^{2} = m$ D、 ${(m + 1)}^{2} = m^{2} + 1$

查看试题解析
7. 如图，有一块含有30°角的直角三角板的两个顶点放在直尺的对边上．如果∠2=44°，那么∠1的度数是（　　）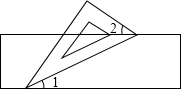

A、14° B、15° C、16° D、17°

查看试题解析
8. 已知 $(x - 2) (x + 3) = x^{2} + m x - 6$ ，则m的值是（）

A、-1 B、1 C、5 D、-5

查看试题解析
9. 如图，有A，B，C三种卡片，其中A型卡片是边长为 $a$ 的正方形，B型卡片是长为 $b$ ，宽为 $a$ 的长方形（ $b > a$ ），C型卡片是边长为 $b$ 的正方形．如果要用它们拼成边长为( $3 a + 2 b$ )的正方形，则需A、B、C三种卡片共（）张．

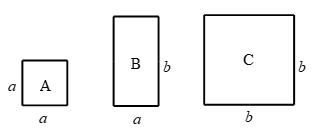A、23 B、24 C、25 D、26

查看试题解析
10. 已知甲、乙两人分别从 $A ， B$ 两地同时匀速出发，若相向而行，则经过a分钟后两人相遇：若同向而行，则经过b分钟后甲追上乙.若甲、乙的速度比为 $10 ： 3$ ，则 $\frac{a}{b}$ 的值为（）

A、 $\frac{13}{7}$ B、 $\frac{7}{13}$ C、 $\frac{5}{3}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题

11. 如果a+b＝8，a²－b²＝24，那么a－b＝．

查看试题解析
12. 分解因式： $3 x^{2} - 27$ = ．

查看试题解析
13. 分式 $\frac{x^{2} - 9}{x^{2} + 3 x}$ 的值为0，则x的值是．

查看试题解析
14. 某实验中学九年级(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示，其中评价为“A”所在扇形的圆心角是度.

查看试题解析
15. 小亮解方程组 ${\begin{matrix} 2 x + y = • \\ 2 x - y = 12 \end{matrix}$ 的解为 ${\begin{matrix} x = 5 \\ y = ★ \end{matrix}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数 $•$ 和★，请你帮他找回 $•$ 这个数， $•$ =.

查看试题解析
16. 如图，两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②、已知大长方形的长为a，则图②阴影部分周长与图①阴影部分周长的差是．

查看试题解析

三、解答题

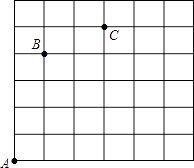
17. 计算：

(1)、（2x）³•y³+16xy²

(2)、（x+2）（2x﹣3）﹣x（x+1）

查看试题解析
18.

(1)、解分式方程： $\frac{x}{x - 3} - 4 = \frac{3}{x - 3}$ ；

(2)、解二元一次方程组 ${\begin{array}{l} 2 x + y = 3 \\ 4 x - 3 y = 11 \end{array}$

查看试题解析
19. 先化简，再求值， $(1 - \frac{2 x y - 2 y^{2}}{x^{2} - y^{2}}) \cdot (x + y)$ ，其中 $x - y = 4$ .

查看试题解析
20. 对于有理数 $x ， y$ ，定义一种新的运算“*”： $x * y = a x + b y + c$ ，其中 $a ， b ， c$ 为常数，等式右边是通常的加法与乘法运算，已知 $3 * 5$ ＝15， $4 * 7$ ＝28，求 $1 * 1$ 的值

查看试题解析
21. 若在方格（每小格正方形边长为1m）上沿着网格线平移，规定：沿水平方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿竖直方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．例如：点A按“平移量”{1，4}可平移至点B．

(1)、从点C按“平移量”{ ， }可平移到点B；

(2)、若点B依次按“平移量”{4，﹣3}、{﹣2，1}平移至点D，
①请在图中标出点D；（用黑色水笔在答题卡上作出点D）
②如果每平移1m需要2.5秒，那么按此方法从点B移动至点D需要多少秒？
③观察点D的位置，其实点B也可按“平移量”{ ， }直接平移至点D；观察这两种平移的“平移量”，猜想：点E依次按“平移量”{2a，3b}、{﹣5a，b}、{a，﹣5b}平移至点F，则相当于点E按“平移量”{ ， }直接平移至点F．

查看试题解析
22. 某校为了解学生的课外阅读情况，对部分学生进行了调查，并统计他们平均每天的课外阅读时间t（单位：min），然后利用所得数据绘制如下两幅不完整的统计图.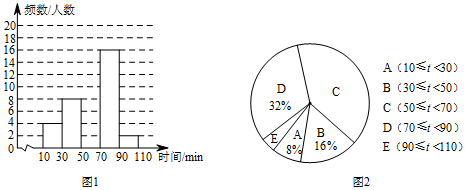

请你根据以上信息解答下列问题：

(1)、本次调查活动采取了调查方式，样本容量是.

(2)、图2中C的圆心角度数为 ▲度，补全图1的频数分布直方图.

(3)、该校有900名学生，估计该校学生平均每天的课外阅读时间不少于50min的人数.

查看试题解析
23. 已知直线AB平行CD，直线EF分别截AB、CD于点E、F两点。

(1)、如图①，有一动点P在线段CD之间运动（不与C，D两点重合），试探究∠1、∠2、∠3的等量等关系？试说明理由。

(2)、如图②、③，当动点P在线段CD之外运动（不与C，D两点重合），问上述结论是否还成立？若不成立，试写出新的结论并说明理由。

查看试题解析
24. 第19届亚运会将于2022年在杭州举行，“丝绸细节”助力杭州打动世界.杭州丝绸公司为亚运会设计手工礼品，投入 $W$ 元钱，若以2条领带和1条丝巾为一份礼品，则刚好可制作600份礼品；若以1条领带和3条丝巾为一份礼品，则刚好可制作400份礼品.

(1)、若 $W = 24$ 万元，求领带及丝巾的制作成本是多少？

(2)、若用 $W$ 元钱全部用于制作领带，总共可以制作几条？

(3)、若用 $W$ 元钱恰好能制作300份其他的礼品，可以选择 $a$ 条领带和 $b$ 条丝巾作为一份礼品（两种都要有），请求出所有可能的 $a$ 、 $b$ 的值.

查看试题解析