浙江省2021年七年级下学期数学期末模拟(嘉兴、金华、湖州、丽水、衢州、舟山适用)
试卷更新日期:2021-06-27 类型:期末考试
一、选择题
-
1. 要使分式有意义,x必须满足的条件是( )A、x≠3 B、x≠0 C、x>3 D、x=32. 如图,三角板的直角顶点落在矩形纸片的一边上.若 ,则 的度数是( )
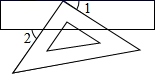 A、 B、 C、 D、3. 计算2x3•(﹣x2)的结果是( )A、2x B、﹣2x5 C、2x6 D、x54. 下面的多项式中,能因式分解的是( )A、 B、 C、 D、5. 某种细胞的直径是0.000067厘米,将0.000067用科学记数法表示为( )A、67×10-6 B、6.7×10-6 C、0.67×10-5 D、6.7×10-56. 大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90-110这一组的频数是( )A、2 B、4 C、6 D、147. 已知: 是一个完全平方式,则 的值为( )A、2 B、 C、1 D、1或-38. 若10y=5,则102﹣2y等于( )A、75 B、4 C、﹣5或5 D、9. 在中央电视台2套“开心辞典”节目中,有一期的某道题目是:如图所示,天平中放有苹果、香蕉、砝码,且两个天平都平衡,则一个苹果的重量是一个香蕉的重量的( )
A、 B、 C、 D、3. 计算2x3•(﹣x2)的结果是( )A、2x B、﹣2x5 C、2x6 D、x54. 下面的多项式中,能因式分解的是( )A、 B、 C、 D、5. 某种细胞的直径是0.000067厘米,将0.000067用科学记数法表示为( )A、67×10-6 B、6.7×10-6 C、0.67×10-5 D、6.7×10-56. 大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90-110这一组的频数是( )A、2 B、4 C、6 D、147. 已知: 是一个完全平方式,则 的值为( )A、2 B、 C、1 D、1或-38. 若10y=5,则102﹣2y等于( )A、75 B、4 C、﹣5或5 D、9. 在中央电视台2套“开心辞典”节目中,有一期的某道题目是:如图所示,天平中放有苹果、香蕉、砝码,且两个天平都平衡,则一个苹果的重量是一个香蕉的重量的( ) A、倍 B、倍 C、2倍 D、3倍10. 在矩形ABCD内,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .当 时, 的值是( )
A、倍 B、倍 C、2倍 D、3倍10. 在矩形ABCD内,将两张边长分别为a和b( )的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .当 时, 的值是( )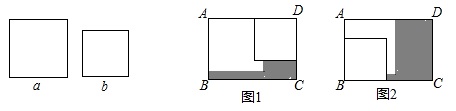 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若a﹣b=1,则代数式2a﹣2b﹣1的值为 .12. 如图,已知AB∥CD,∠1=120°,则∠C=.
 13. 分解因式:
13. 分解因式: = 14. 计算:15. 若 则 的值是16. 已知(x﹣2)x+4=1,则x的值可以是 .
= 14. 计算:15. 若 则 的值是16. 已知(x﹣2)x+4=1,则x的值可以是 .三、解答题
-
17. 计算下列各题:(1)、(m2n4)×(3m2n)÷(-mn2)2(2)、(3x+2)2-(3x-1)(1+3x)18. 把下列多项式因式分解(1)、6a2+12ab+6b2(2)、2a(x2+4)2-32ax2 .19. 若方程组 与 有公共解,求a+b的值20. 解方程或方程组:(1)、 ;(2)、 .21. 某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下:
人数
1
2
4
3
2
每人所作标本数
2
4
6
8
10
根据表中提供的信息,回答下列问题:
(1)、该组共有学生多少人?(2)、制作标本数在6个及以上的人数在全组人数中所占比例?(3)、平均每人制作多少个标本?(4)、补全下面的条形统计图. 22. 云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
22. 云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载) (1)、若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?(2)、为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?23. 某市为创建生态文明城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,有三种施工方案:
(1)、若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?(2)、为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?23. 某市为创建生态文明城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,有三种施工方案:方案一:甲队单独完成这项工程,刚好能如期完成;
方案二:乙队单独完成这项工程,要比预定工期多用3天;
方案三:先由甲、乙两队一起合作2天,剩下的工程由乙队单独完成,刚好如期完成。
(1)、求工程预定工期的天数(2)、若甲队每施工一天需工程款2万元,乙队每施工一天需工程款1.3万元.为节省工程款,同时又如期完工,请你选择一种方案,并说明理由24. 已知:三角形ABC和三角形DEF位于直线MN的两侧中,直线MN经过点C , 且 ,其中 , , ,点E、F均落在直线MN上. (1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)
(1)、如图1,当点C与点E重合时,求证: ;聪明的小丽过点C作 ,并利用这条辅助线解决了问题.请你根据小丽的思考,写出解决这一问题的过程.(2)、将三角形DEF沿着NM的方向平移,如图2,求证: ;(3)、将三角形DEF沿着NM的方向平移,使得点E移动到点 ,画出平移后的三角形DEF , 并回答问题,若 ,则 . (用含 的代数式表示)