浙江省2021年七年级下学期数学期末模拟(宁波、绍兴、台州适用）

试卷更新日期：2021-06-27 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分.）

1. 若分式 $\frac{x - 2}{x + 3}$ 有意义，则x的取值范围是（　　）

A、x≠-3 B、x≥-3 C、x≠-3且 x≠2 D、x≠2

查看试题解析
2. 随着京雄城际铁路全线贯通，雄安站同步投入运营，雄安站是京雄城际铁路的终点站，也是雄安新区第一个开工建设的大型基础设施工程，该站为桥式站，主体共5层，其中地上3层、地下2层，总建筑面积475000平方米．将475000用科学记数法表示为（）

A、 $4.75 \times 10^{4}$ B、 $4.75 \times 10^{5}$ C、 $47.5 \times 10^{4}$ D、 $47.5 \times 10^{5}$

查看试题解析
3. 下列运算正确的是（）

A、a²•a³=a⁶ B、﹣2（a﹣b）=﹣2a﹣2b C、2x²+3x²=5x⁴ D、（﹣ $\frac{1}{2}$ ）^﹣2=4

查看试题解析
4. 如图， $B D / / C E$ ， $∠ 1 = 80 °$ ， $∠ 2 = 30 °$ ，则 $∠ A$ 的度数是（）

A、 $110 °$ B、 $30 °$ C、 $50 °$ D、 $80 °$

查看试题解析
5. 化简 $\frac{a}{a - 1}$ + $\frac{1}{1 - a}$ 的结果为（）

A、1 B、﹣1 C、 $\frac{a + 1}{a - 1}$ D、 $\frac{a + 1}{- a + 1}$

查看试题解析
6. 方程组 ${\begin{matrix} 2 x + y = Δ \\ x + y = 3 \end{matrix}$ 的解为 ${\begin{matrix} x = 1 \\ y = \nabla \end{matrix}$ ，则被遮盖的 $Δ$ 、 $\nabla$ 的两个数分别为（）

A、1，2 B、1，3 C、2，3 D、4，2

查看试题解析
7. 若x²+（m﹣2）x+9是一个完全平方式，则m的值是（）

A、8 B、﹣8 C、8或﹣8 D、8或﹣4

查看试题解析
8. 如图，∠BCD＝70°，AB∥DE ，则∠α与∠β满足（　　）

A、∠α+∠β＝110° B、∠α+∠β＝70° C、∠β﹣∠α＝70° D、∠α+∠β＝90°

查看试题解析
9. 杨辉三角形，又称贾宪三角形、帕斯卡三角形，是二项式系数在三角形中的一种几何排列 $.$ 在我国南宋数学家杨辉所著的 $《$ 解：九章算术 $》 (� 1261$ 年 $)$ 一书中用如图的三角形解释二项和的乘方规律.观察下列各式及其展开式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2} {(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3} {(a + b)}^{4}$
$= a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4} {(a + b)}^{5}$

$= a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5} \dots$ ；请你猜想 ${(a + b)}^{10}$ 展开式的第三项的系数是（）

A、36 B、45 C、55 D、66

查看试题解析
10. 如图，直角梯形纸片对边 $A B // C D$ ， $∠ C$ 是直角，将纸片沿着EF折叠，DF的对应边 $D^{'} F$ 交AB于点G，FH平分 $∠ C F D^{'}$ 交AC于点H.则结论：① $∠ A G F = 2 ∠ G F E$ ；② $∠ E G F = ∠ G F E$ ；③ $∠ C H F = ∠ G F E$ ；④若 $∠ B^{'} E G = 70 °$ ，则 $∠ G F E = 55 °$ .其中正确结论的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（本大题有6小题，每小题3分，共18分.）

11. 分解因式：(a－b)²－4b²＝．

查看试题解析
12. 要使分式 $\frac{1 - x}{x - 2}$ 的值为0，则x的值为.

查看试题解析
13. 已知关于x，y的方程组 ${\begin{cases} x + 2 y = k \\ 2 x + 3 y = 3 k - 1 \end{cases}$ ，有以下结论：①当k=0时，方程组的解是 ${\begin{matrix} x = - 2 \\ y = 1 \end{matrix}$ ；
②方程组的解可表示为 ${\begin{matrix} x = 3 k - 2 \\ y = 1 - k \end{matrix}$ ；③不论k取什么实数， $x + 3 y$ 的值始终不变.

其中正确的有．（填写编号）

查看试题解析
14. 已知 $a + b = - 5$ ， $b - c = 1$ ，则 $(b + c) - (1 - 2 a)$ 的值为.

查看试题解析
15. 如图，长方形纸片的长为6cm，宽为4cm，从长方形纸片中剪去两个形状和大小完全相同的小长方形卡片，那么余下的两块阴影部分的周长之和是.

查看试题解析
16. 如图，已知点C为两条相互平行的直线AB，ED之间一点， $∠ A B C$ 和 $∠ C D E$ 的角平分线相交于F，若∠BCD= $\frac{3}{2}$ ∠BFD+10°，则 △BCD 的度数为．

查看试题解析

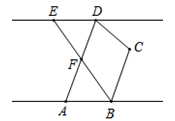
三、解答题：本大题有8小题，第17-18题每题5份，第19-22题每题6分，第23题8分，第24题10分.）

17. 化简与计算：

(1)、 ${(- \frac{1}{3})}^{- 1} - {(- 3)}^{2} + {(π - 2)}^{0}$

(2)、（﹣2a³）³+（﹣4a）²•a⁷﹣2a¹²÷a³

查看试题解析
18. 解下列方程：

(1)、3x+3＝2x﹣1；

(2)、 $\frac{x + 3}{2} - x = \frac{2 x + 1}{3}$ .

查看试题解析
19. 化简并求值．

(1)、2（2x-3y）-（3x+2y+1），其中x=2 ，y=-0.5 ；

(2)、 $\frac{1}{3}$ (9ab²－3)＋(7a²b－2)＋2(ab²－1)－2a²b ，其中a＝－2，b＝3．

查看试题解析
20. 在网格上，平移△ABC，并将△ABC的一个顶点A平移到点D处，

(1)、请你作出平移后的图形△DEF；

(2)、请求出△DEF的面积（每个网格是边长为1的正方形）.

查看试题解析
21.

(1)、请在横线上填写合适的内容，完成下面的证明：
如图①如果AB∥CD，求证：∠APC＝∠A+∠C．

证明：过P作PM∥AB ．

所以∠A＝∠APM ， (    ▲    )

因为PM∥AB ， AB∥CD(已知)

所以∠C＝    ▲    (    ▲    )

因为∠APC＝∠APM+∠CPM

所以∠APC＝∠A+∠C(等量代换)

(2)、如图②，AB∥CD，根据上面的推理方法，直接写出∠A+∠P+∠Q+∠C＝．

(3)、如图③，AB∥CD，若∠ABP＝x，∠BPQ＝y，∠PQC＝z，∠QCD＝m，则m＝(用x、y、z表示)

查看试题解析
22. 列方程组解应用题，为了保护环境，深圳某公交公司决定购买一批共10台全新的混合动力公交车，现有A、B两种型号，其中每台的价格，年省油量如下表：

A

B

价格（万元/台）

a

b

节省的油量（万升/年）

2.4

2

经调查，购买一台A型车比购买一台B型车多20万元，购买2台A型车比购买3台B型车少60万元．

(1)、请求出a和b；

(2)、若购买这批混合动力公交车每年能节省22.4万汽油，求购买这批混合动力公交车需要多少万元？

查看试题解析
23. [数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片.

实验目的：

用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.

例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积，写出相应的等式有a²+3ab+2b²=（a+2b）（a+b）或（a+2b）（a+b）=a²+3ab+2b².

问题探索：

(1)、小明想用拼图的方法解释多项式乘法（2a+b）（a+b）=2a²+3ab+b² ，那么需要两种正方形纸片张，长方形纸片张；

(2)、选取正方形、长方形硬纸片共8块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；

(3)、试借助拼图的方法，把二次三项式2a²+5ab+2b²分解因式，并把所拼的图形画在虚线方框3内.

查看试题解析
24. 南浔区某校组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动，基地离学校有120千米，队伍乘大巴车8：00从学校出发.苏老师因有事情，8：30从学校自驾小汽车以大巴车1.5倍的速度追赶，追上大巴车后继续前行，结果比队伍提前10分钟到达基地.问：

(1)、设大巴午的平均速度是x(km／h)，利用速度、时间和路程之间的关系填写下表.(要求：填上适当的代数式，完成表格)(温馨提示：请填写在答题卷相对应的表格内)

速度（km/h）

路程（km）

时间（h）

大巴车

x

120

小汽车

120

(2)、列出方程，并求出大巴车与小汽车的平均速度.

(3)、当苏老师追上大巴车时，大巴车离基地还有多远?

查看试题解析

	A	B
价格（万元/台）	a	b
节省的油量（万升/年）	2.4	2

	速度（km/h）	路程（km）	时间（h）
大巴车	x	120
小汽车		120