浙江省2021年七年级下学期数学期末模拟(杭州适用）

试卷更新日期：2021-06-27 类型：期末考试

进入出卷网下载

一、选择题（共10小题）.

1. $3^{- 2}$ 等于（）

A、-9 B、-6 C、9 D、 $\frac{1}{9}$

查看试题解析
2. 下列调查中，最适合采用全面调查的是（）

A、对全国中学生睡眠时间的调查 B、对我市各居民日平均用水量的调查 C、对光明中学七（1）班学生身高的调查 D、对某批次灯泡使用寿命的调查

查看试题解析
3. 化简：（﹣2）²⁰⁰³+（﹣2）²⁰⁰²所得的结果为（）

A、2²⁰⁰² B、﹣2²⁰⁰² C、﹣2²⁰⁰³ D、2

查看试题解析
4. 下列运算正确的是（）

A、 $a^{5} + a^{2} = a^{7}$ B、 ${(- a^{6})}^{3} = a^{18}$ C、 $a^{0} \div a^{- 3} = a^{3}$ D、 $a^{6} - a^{2} = a^{4}$

查看试题解析
5. 下面式子从左边到右边的变形是因式分解的是（　　）

A、x²﹣x﹣2＝x（x﹣1）﹣2 B、x²﹣4x+4＝（x﹣2）² C、（x+1）（x﹣1）＝x²﹣1 D、x﹣1＝x（1﹣ $\frac{1}{x}$ ）

查看试题解析
6. 如图，已知AB∥CD，DB⊥BC，∠1=40°，则∠2的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
7. 已知方程组 ${\begin{array}{l} x + y = 3 \\ m x - y = 5 \end{array}$ 的解是方程x﹣y=1的一个解，则m的值是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，若△DEF是由△ABC经过平移后得到，已知A ， D之间的距离为1，CE＝2，则EF是（　　）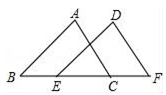

A、1 B、2 C、3 D、4

查看试题解析
9. 现要装配30台机器，在装配好6台以后，采用了新的技术，每天的工作效率提高了一倍，结果共用了3天完成任务，求原来每天装配机器的台数x，下列所列方程中正确的是（　　）

A、 $\frac{6}{x} + \frac{24}{2 x} = 3$ B、 $\frac{6}{x} + \frac{24}{x + 2} = 3$ C、 $\frac{6}{x} + \frac{30}{2 x} = 3$ D、 $\frac{30}{x} + \frac{30}{2 x} = 3$

查看试题解析
10. 某商店搞促销活动，同时购买一个篮球和一个足球可以打八折，需花费1280元.已知篮球标价比足球标价的3倍多15元，若设足球的标价是x元，篮球的标价为y元，根据题意，可列方程组为（）

A、 ${\begin{cases} y - 3 x = 15 \\ 0.2 (x + y) = 1280 \end{cases}$ B、 ${\begin{cases} y - 3 x = 15 \\ 0.8 (x + y) = 1280 \end{cases}$ C、 ${\begin{cases} 3 x - y = 15 \\ 0.2 (x + y) = 1280 \end{cases}$ D、 ${\begin{cases} 3 x - y = 15 \\ 0.8 (x + y) = 1280 \end{cases}$

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

11. 因式分解： $a^{2} - 1$ =.

查看试题解析
12. 当a=时，分式 $\frac{3}{a + 2}$ 没有意义．

查看试题解析
13. 已知 $x = \sqrt{2} + 1$ ，则代数式 $x^{2} - 2 x + 1$ 的值为.

查看试题解析
14. 小明将同学们周末生活的调查结果绘制成了扇形统计图.其中，看书这一项对应的圆心角度数为72°，则周末看书的同学人数占了总数的． ( 填百分比 )

查看试题解析
15. 如图，AB∥CD，FE⊥DB，垂足为E，∠1＝50°，则∠2的度数是.

查看试题解析
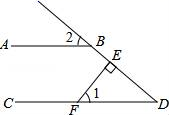16. 小威到小吃店买水饺,他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱,若小威先买了9粒虾仁水饺,则他身上剩下的钱恰好可买粒韭菜水饺.

查看试题解析

三、解答题：本大题有7个小题.共66分.

17. 化简与计算：

(1)、 ${(- \frac{1}{3})}^{- 1} - {(- 3)}^{2} + {(π - 2)}^{0}$

(2)、（﹣2a³）³+（﹣4a）²•a⁷﹣2a¹²÷a³

查看试题解析
18. 解方程组：

(1)、 ${\begin{cases} 2 x - 5 y + 13 = 0 \\ 9 x + 6 y - 8 = 0 \end{cases}$

(2)、 ${\begin{cases} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{cases}$

查看试题解析

19. 某学校随机抽取部分学生，调查每个月的零花钱消费额，数据整理成如下的统计表和如图①②所示的两幅不完整的统计图，已知图①中A，E两组对应的小长方形的高度之比为2：1．请结合相关数据解答以下问题：月消费额分组统计表

组别	月零花钱消费额/元
A	10≤x＜100
B	100≤x＜200
C	200≤x＜300
D	300≤x＜400
E	x≥400

(1)、本次调查样本的容量是；

(2)、补全频数分布直方图，并标明各组的频数；

(3)、若该学校有2500名学生，请估计月消费零花钱不少于300元的学生的数量．

查看试题解析

20. 先化简，再求 $\frac{2 (a + b)}{a - b} + \frac{3 b}{2 a + 2 b} + \frac{a b + 7 b^{2}}{2 a^{2} - 2 b^{2}}$ 的值，其中a= $\frac{49}{4}$ ，b=﹣ $\frac{31}{4}$ ．

查看试题解析
21. 阅读材料：
我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b)$ $- 2 (a + b) + (a + b)$ = $(4 - 2 + 1) (a + b) = 3 (a + b)$ .“整体思想”是初中数学解题中的一种重要的思想方法，它在多项式的化简与求职中应用极为广泛.

尝试应用：

(1)、把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 6 {(a - b)}^{2} + 2 {(a - b)}^{2}$ 的结果为.

(2)、已知 $x^{2} - 2 x = 4$ ，求 $- 3 x^{2} + 6 x - 21$ 的值.

(3)、已知 $a - 2 b = 3 ， 2 b - c = 5 ， c - d = 10$ ，求 ${(a - c)}^{3} + {(2 b - d)}^{2} - (2 b - c)$ 的值.

查看试题解析

22. 为了创建国家卫生城市，需要购买甲、乙两种类型的分类垃圾桶替换原来的垃圾桶，

A

，

B

，

C

三个小区所购买的数量和总价如表所示.

	甲型垃圾桶数量（套）	乙型垃圾桶数量（套）	总价（元）
$A$	$10$	$8$	$3320$
$B$	$5$	$9$	$2860$
$C$	$a$	$b$	$2580$

(1)、问甲型垃圾桶、乙型垃圾桶的单价分别是每套多少元？

(2)、求

a

，

b

的值.

查看试题解析

23. 如图

(1)、如图1，要使 $A B / / C D$ ， $∠ B$ 、 $∠ P$ 、 $∠ C$ 应满足的数量关系是.

(2)、 $A B / / C D$ ，直线MN分别与AB、CD交于点M、N，平面内一点P满足 $∠ A M P = 2 ∠ A M N = 2 α$ ，
①如图2，若 $NP ⊥ MP$ 于点P，判断 $∠ PNC$ 与 $∠ PMB$ 的数量关系，并说明理由；

②若 $0 < α < 40 °$ ， $∠ M P N = 60 °$ ，求 $∠ P N D ($ 用含 $α$ 的式子表示 $)$ .

查看试题解析